车道被占用时车辆排队长度的计算

谷翠梅，杨 静，王丽婷，李爱玲

(河北北方学院 理学院,河北 张家口 075000)

道路堵塞时车辆排队现象时有发生，因此学者们一直致力于排队现象的分析和排队长度的计算。分析方法主要包括概率论、随机过程、排队论、神经网络、冲击波等。概率论方法认为车辆到达和离去服从某种概率分布，车辆到达数和离去数之差为排队车辆数[1]。随机过程使用马尔卡夫链方法得到信号交叉口队列长度的时变概率分布及其时间序列函数[2]。排队论把车辆在路段上的行驶过程看作排队系统中的接收或等待服务，认为等待服务即开始排队，由排队论得到各种排队系统的平均车辆数[3]。神经网络利用模拟数据或调查数据对网络进行训练来获得输入变量与排队长度之间的对应关系[4-5]。冲击波方法认为当车速为0时加入排队队列，通过停车波波速的传播时间来预测排队长度[6]。

从排队分析的方法可以看出，基于不同的排队模型，通过使用不同的计算方法，可以得到不同的排队长度计算结果[7]。本文建立了基于停车波和启动波的车辆排队长度计算模型和基于二流理论的拥挤交通流单车道当量排队长度计算模型。

根据公路工程技术标准中标准车的计算公式可知：大车=2.5倍标准车，标准车=2.5倍小车。通过观测某一地段左侧车道和中间车道的车辆数可得到表1。

表1 左侧车道和中间车道观测数据

1 基于停车波和启动波模型的车辆排队长度计算

定义1.1[8]传统的停车波与启动波的格林希尔治模型

式中kj为阻塞密度;vf为自由流速度。

由于传统的格林希尔治停车波与启动波模型在较大交通流密度情况下存在一定偏差，对其进行改进后，得到改进的停车波与启动波的格林伯速度密度模型

式中vm为交通流达到通行能力时的速度(km·h-1)。

对于停车波结合波速公式得

式中k1为停车密度。

同理，可得启动波为

式中k2为启动密度。

又因为排队持续时间tj=t0+ts，其中t0为停车波开始产生到启动波产生的时间(h)，ts为排队消散时间(h)。

因此，根据停车波与启动波相遇的位置(即排队消散的位置)能够得出排队消散时间的计算公式为

|v1′|(t0+ts)=|v2′|ts

将改进的停车波和启动波公式带入可得

排队消散时间

排队持续时间

则最大排队长度L

L=|v1′|tj=|v2′|ts

根据表1首先得出7个时间段的阻塞密度和启动密度，并由改进的停车波与启动波的格林伯速度密度模型计算出排队长度(表2)。

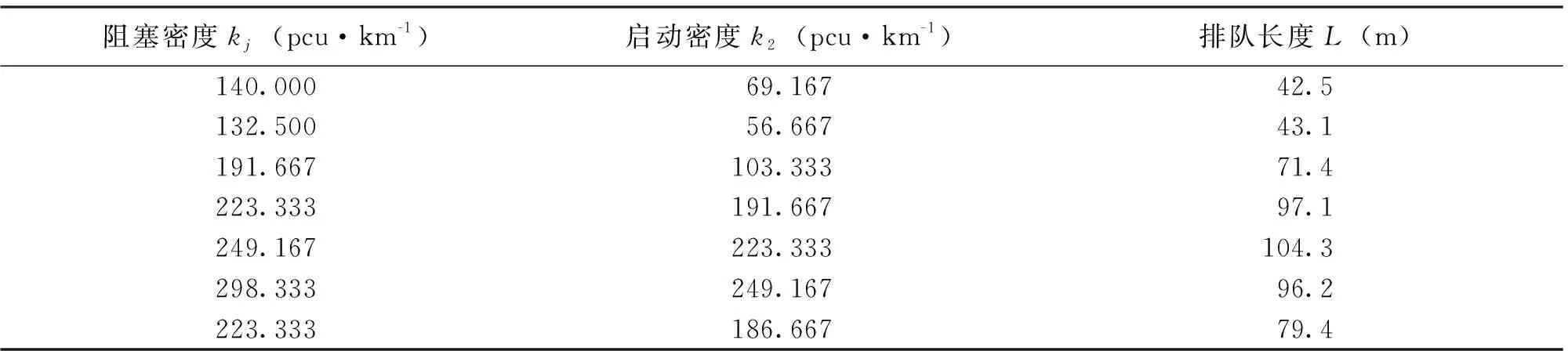
表2 改进的停车波与启动波的格林伯速度密度模型计算出的排队长度

2 基于二流理论的拥挤交通流单车道当量排队长度计算

定义2.1[9]由流量守恒定律可得N0+NU(t)=ND(t)+ΔN(t),式中N0为初始时刻上、下游断面之间的车辆数，NU(t)为t时刻通过上游断面的车辆累计数，ND(t)为t时刻通过下游断面的车辆累计数；ΔN(t)为t时刻上、下游断面之间的车辆数。

在ΔN(t)的计算过程中，应用二流理论可得ΔN(t)=kjLD(t)+km[L-LD(t)],式中km为上、下游断面之间的交通流最佳密度，kj为阻塞密度，L为上、下游断面之间的距离，LD(t)为当量排队长度。因此

此式即为基于二流理论的拥挤交通流单车道当量排队长度模型。

通过观测某一路段上、下游的车辆数可得到表3。

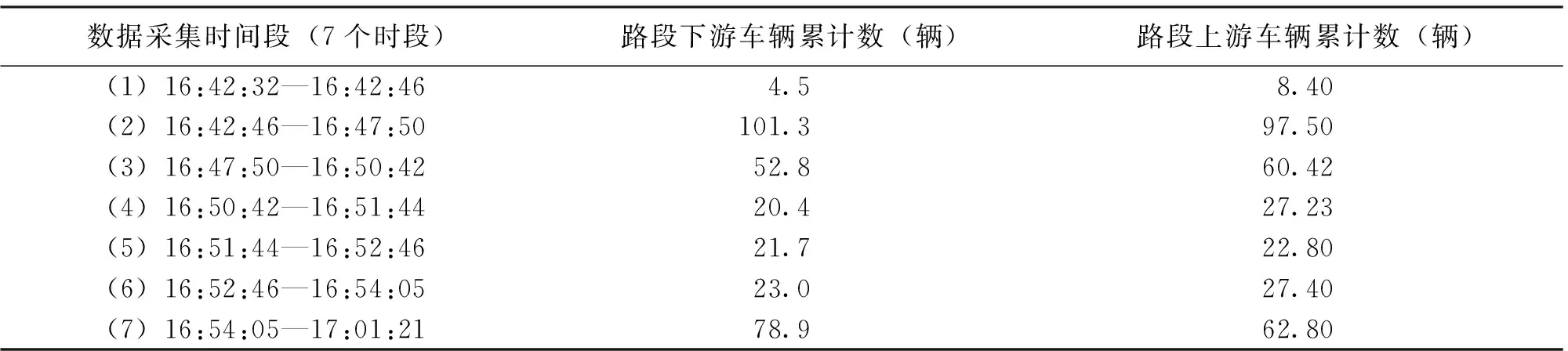
表3 上、下游车辆数观测数据

根据定义2.1可得出上、下游断面之间的交通流阻塞密度kj为160.667(pcu·km-1),观测此路段上、下游断面之间的距离L为120 m，初始时刻上、下游断面之间的车辆数为16.667辆，而上、下游断面之间的交通流最佳密度可以利用交通流理论中的Greenshields模型计算。计算公式为

表4 t时刻上、下游断面之间的当量排队长度

因为畅行速度vf，阻塞密度kj，启动密度K均已在改进的停车波与启动波的格林伯速度密度模型中得出，分别为vf、kj、ki，因此可以算出交通流最佳密度V=43.490(pcu·km-1)；进而可以算出t时刻上、下游断面之间的当量排队长度(分为7个时间段)，结果见表4。

3 结果分析

将上述2个模型所得排队长度进行比较得出图1。

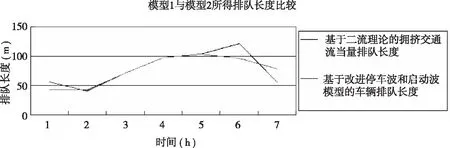
图1 两个模型所得排队长度

由图1看出基于停车波和启动波的车辆排队长度模型在道路堵塞密度较大的情况下模拟程度较好，而对于车流比较顺畅的第一、第六和第七阶段模拟程度并不是很好；同时也验证了基于二流理论的拥挤交通流单车道当量排队长度计算的正确性。因此采用基于二流理论的拥挤交通流单车道当量排队长度计算结果中的第一、第六和第七时间段的计算结果和基于停车波和启动波模型的车辆排队长度计算结果中其他4个时间段的计算结果作为排队长度最终的计算结果(表5)。

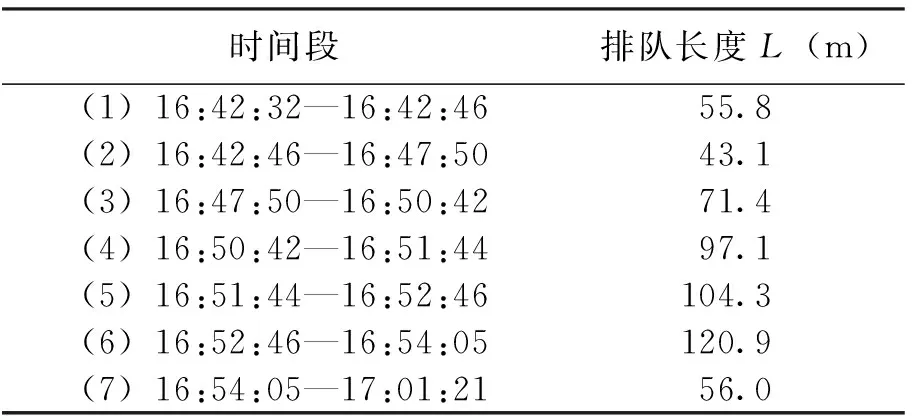
表5 排队长度

4 结论与讨论

本文通过建立两种不同的车辆排队长度计算模型，进行互相验证，得出相应的结论。基于停车波与启动波的车辆排队长度模型在道路车流拥堵密度较大的情况下比较适用，而在道路车流交通畅通情况下应采用基于二流理论的车辆排队长度模型进行计算。此研究结果可以为交通管理与控制部门采取交通管控提供依据。