使用贪心模拟退火算法求解WTA问题

傅 勉,王丹丹

(安徽新华学院 商学院，安徽 合肥 230088)

0 引 言

武器-目标分配(weapon-target assignment,WTA)是管理学领域中的一个经典难题。随着武器-目标分配问题规模的扩大，它的解也会空前巨大，使得武器-目标分配问题成为了NP难题。很多学者尝试使用智能算法解决WTA问题，文献[1]使用蚁群算法求解WTA问题，文献[2]使用模拟退火算法求解WTA问题，但都是针对武器数量和目标数量，是一一对应的这种特殊情况进行计算的。文献[3]使用遗传算法求解WTA问题，但目标所分配的武器数量是事先确定的，不是十分符合现实情况。文献[4]使用神经网络算法求解WTA问题，但求解质量不是很高。基于当前智能算法在求解WTA问题上的不足，本文提出将贪心机制融入模拟退火算法中，通过不断贪心寻优得到WTA问题的最优解。

1 WTA问题

现有WTA问题描述为武器m个，目标n个，它们之间关系是1个武器必须且只能对应1个目标，1个武器最多可以打击Ri个目标(i=1，…，n)，1个目标最多可以被Sj(j=1,2…,m)个武器打击。Pij(i=1,2...,m;j=1,2…,n)表示武器对目标的命中概率，Xij表示某武器是否打击某目标，1表示打击，0表示不打击。最优目标是武器打击所有目标的成功概率最大。构建WTA问题模型如下

(1)

2 贪心模拟退火算法设计思想

贪心模拟退火算法的思想是基于模拟退火算法容易陷入局部最优解这一缺陷，将贪心思想融入模拟退火算法中，在每次模拟退火算法产生新解后对其进行局部贪心搜索，寻找到更优解，进而提高求解质量。

2.1 解编码确定

为了实现成功概率最大目标，把全部的m个武器用于打击所有目标，那么解的编码长度就是武器数目m，使用整数编码方式，将解记为A=c1,c2,…,ci，…，cn，其中ci指的是第i个武器打击目标的具体编号，因此，这个解就是每个武器对应的打击目标的具体编号。举例说明：解(1 2 3 2)表示4个武器，打击的是3个目标；具体分配是武器1打击目标1，武器2、4打击目标2，武器3打击目标3。

2.2 目标函数

根据前面WTA问题描述的目标，可以把最大成功概率、最小失败概率建立目标函数

(2)

2.3 新解的产生与接受准则

2.3.1 新解的产生

产生新解主要是2种策略交叉使用产生，每次运行时会随机使用某一个策略生成新的解。策略1是两点翻转策略，主要过程：在某一个解编码串中随机地确定2个点，然后将2点之间的编码翻转顺序逆序排列，比如原始解A=1 2 3 2，如果随机选中的是2和3，那么经过翻转策略后，A'=1 3 2 2。可以看出，翻转策略仅仅改变了每个武器对每个打击目标的打击顺序，但没有改变每一个目标实际被分配的具体武器数量。因此，需要考虑WTA中会出现这样一种情况：武器数量大于目标数量，即每一个目标被分配的打击武器数量可以是Sj(j=1,2…,n)个，为了达到原定的成功概率最大这个目标，需要随时地修正打击目标的武器数量。因此，另一个策略是：选择那些打击武器数量超过一个的被打击目标，将解空间中所有的这类目标变更为1-n中的其他目标。比如：原始解A=2 3 1 3，目标是3，其打击武器是武器2和武器4，把第1个目标3转化为打击目标2，因此，产生的新解就是A'=2 2 1 3。

2.3.2 接受准则

本文使用Metropolis作为接受准则，即

(3)

其中，参数Δf是新产生解和当前解的差值，参数t是控制参数。当Δf<0，可以接受新产生解；当Δf≥0时，需要进行以下的判断：随机生成1个0～1之间的随机数，若r大于等于这个随机数，那么接受这个新解；否则，不接受这个新解。

2.3.3 冷却进度表等参数的选择

冷却进度表是控制模拟退火算法的基本参数，主要包括开始温度、结束温度、衰减系数、Markov链的长度和结束规则，合理选择冷却进度表参数是应用该算法的关键环节。在仿真实验中，文章借鉴文献中给出的冷却进度表参数选取[5-6]，通过仿真实验验证得到如下结论：开始温度T对仿真实验结果影响不大，结束温度Tstop最好控制在低于0.01，衰减系数tr选择大于0.9，Markov链长度可以取21～41。衰减函数设置：tk+1=tk*tr。

2.4 贪心机制

把贪心算法思想融入模拟退火算法中提高局部寻优的能力，贪心算法的思想是尽可能使每一个武器都能最大限度地去选择那些能够提高命中概率的打击目标，具体实现步骤：

1)针对具体的WTA问题，按照从大到小的顺序排列所有武器的命中概率，放入1个二维的数组optimal_target[m][n]中。比如说，如果是m=6，n=5这样的一个问题，这个问题有5个目标，需要储存每一个武器的前面3个最优秀目标科，并将其放入二维的数组optimal_target[6][3]里面(表1)。

表1 optimal_target[6][3]数组值

2)如果需要执行贪心算法的解是5、4、1、3、5、2。

3)设定贪心算法执行次数times是1。

4)随机地选择解5、4、1、3、5、2中的某一个位置，如果是位置4，那么对应的是目标3和武器4。

5)在这个二维的数组当中，第4个武器的最优目标是optimal_target[4][1]等于5，它对应的武器是1。然后，计算这2个武器对这个目标的单发命中概率的和为a=P43+P15；如果把武器4的最优良目标5配置给它，那么就需要把目标3和目标5进行互换，然后计算互换后的单发命中概率的和b=P45+P13。如果b大于a，表示该解使得目标函数向更优良发展，那么可以互换目标5和目标3；否则，需要进一步寻找稍弱一点的最优目标optimal_target[4][2]=4，那么得到a=P43+P24。如果互换目标3和目标4之后，算出b=P44+P23，假如b大于a，那么互换目标3和目标4；否则的话，需要继续寻找下一个最优良目标，直到找到best_target[4][3]。

6)若执行次数times>m/2，贪心算法执行结束，转到步骤7；否则，执行次数times增加1次，并且转到步骤(4)。

7)输出贪心算法执行后得到的最优解。

2.5 贪心模拟退火算法描述

步骤1：确定武器-目标分配问题的相关参数m、n、R、S、P，给出冷却进度表的相关参数T、Tstop、tr，链长度Mmax，计算机随机地生成1个开始解；

步骤2：计算初始解的能量值大小；

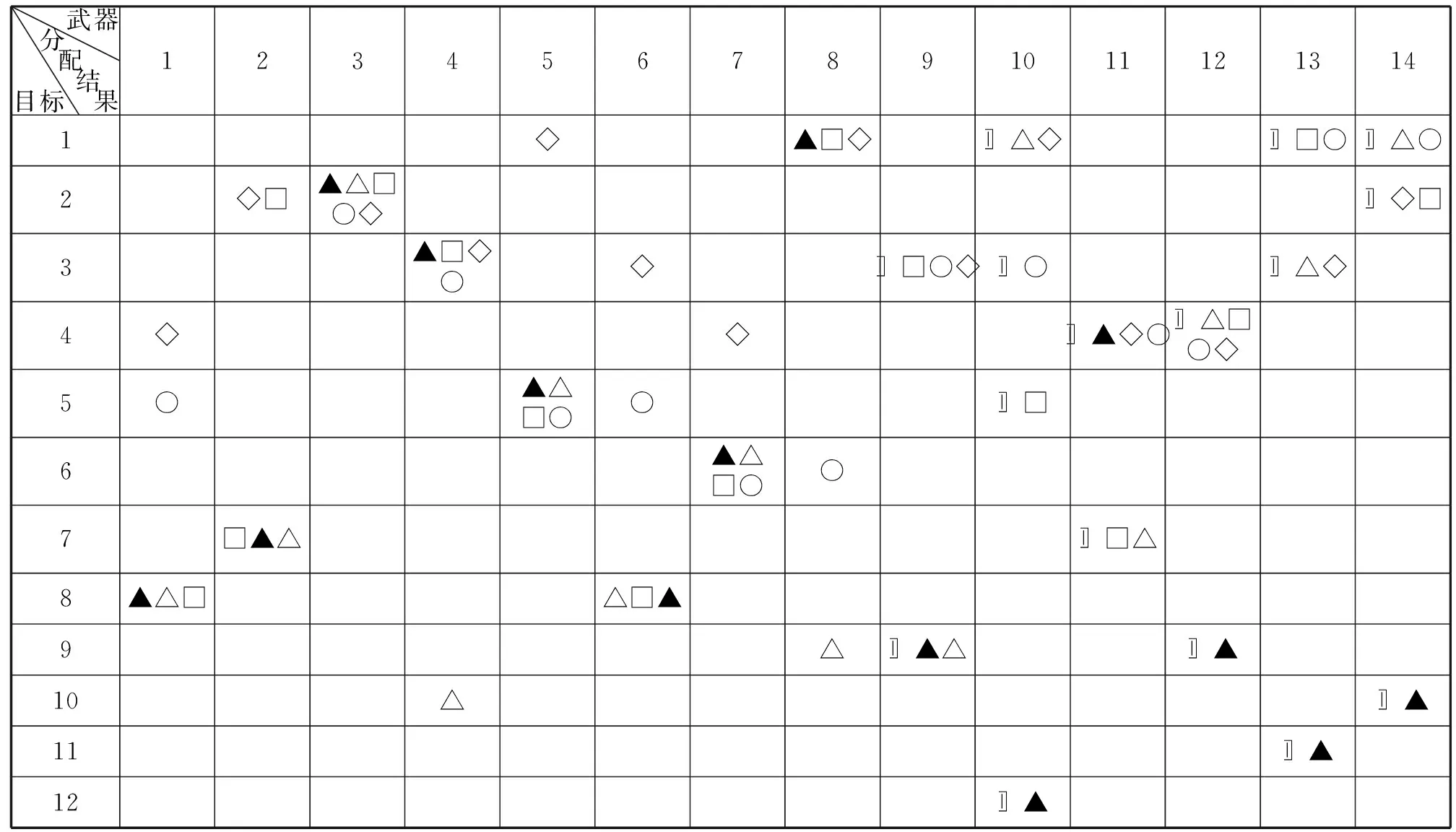
步骤3：如果T

步骤4：如果迭代的次数>Mmax，那么转到步骤9；

步骤5：随机地选择新解产生中的某一个策略以生成新的解，并对这个新产生的解执行贪心寻优过程；

步骤6：计算新产生解的能量值大小，执行前面分析的具体接受准则；

步骤7：保留优化过程中生成的最优解和它的能量值；

步骤8：增加迭代数，然后转到步骤4；

步骤9：计算T=T*tr，迭代次数设置为1，转到步骤3；

步骤10：输出执行得到的最优解和最优能量值。

3 仿真实验

某地舰艇联队有m=14个武器，其攻击的目标数分别是n=12、10、8、6、4个，Sj=4(j=1,2，…,n)。单发命中概率见表2。

表2 命中概率

仿真程序在MATLAB中进行编制。主要使用的基本参数T取1，Tstop取0.01，tr取0.95，Mmax取为20，采用前面构建的贪心模拟退火程序，得到了最优方案(图1)。在图1中，目标数分别是12、10、8、6、4时，使用不同符号(▲△□○◇)表示分配的结果。可以看出，均取得了最优分配方案。

武器分配结果目标12345678910111213141◇▲□◇〛△◇〛□○〛△○2◇□▲△□○◇〛◇□3▲□◇○◇〛□○◇〛○〛△◇4◇◇〛▲◇○〛△□○◇5○▲△□○○〛□6▲△□○○7□▲△〛□△8▲△□△□▲9△〛▲△〛▲10△〛▲11〛▲12〛▲

图1 分配结果图

为了方便比较，分别使用相同的数据采用遗传算法和神经网络算法以及贪心模拟退火算法对上面5个案例进行求解。表3给出这几种算法的求解结果及其比较。很显然，贪心模拟退火算法的求解结果远远优于其他两种算法的结果，证明了本文使用方法的有效性。

表3 不同算法最优值比较

4 结 论

WTA问题是典型的NP难题，文章针对当前学术界在求解WTA问题中存在不足，提出了将贪心算法融入模拟退火算法中，构建了贪心模拟退火算法。仿真实验结果验证了该方法的有效性和可借鉴性。