APFSDS外形变化对阻力系数影响分析

岳 通，王惠源，张成卿

(中北大学 机电工程学院， 太原 030051)

尾翼稳定脱壳穿甲弹(Armor Piercing Fin Stabilized Discarding Sabot,简称APFSDS)在完成脱壳并飞向目标的过程中，应使弹体所受的阻力最小，使其着靶速度更高，这样有利于提高弹体的侵彻效果。近年来，很多学者对弹箭的气动外形进行研究，提出很多降低弹体阻力的方法。头部降阻的研究结果有：头部外形及头部长径比对飞行阻力影响很大，文献[1]通过研究得到某35 mm榴弹在超声速下，冯·卡门曲线母线轮廓的弹丸阻力系数最低；文献[2-3]对圆锥形、切拱形及指数形弹头部形状的气动特性进行了研究,得到指数形的升阻比最大；头部钝化：鼻尖处半径为r的半球状头部代替原来的尖头，文献[4]通过对旋成体弹在高超声速的条件下的实验结果和理论分析得出，当头部钝度取r/R=0.03时，头部钝化后对波阻没有影响。对尾翼降阻的研究结果有：阻力随展弦比的增大而增加，随尾翼相对厚度的增大而增大[5-6]；文献[7]研究了在超音速流动中变展弦比，变曲率半径，变安装角的平面翼与卷弧翼的气动特性,得到平面翼具有更高的升力与俯仰力矩。

在以往的研究中，只是给出降低弹体阻力的方法，然而在弹箭设计中，在给出降阻方法的同时，还需考虑该方法对弹体稳定性的影响规律。本文以尾翼稳定脱壳穿甲弹为研究对象，以弹头部长径比，尾翼根梢比及尾翼后缘后掠角这3个参数对尾翼弹阻力系数及稳定性的影响规律进行定量分析。

1 弹体模型及参数

本节将介绍弹体的几何模型以及相关的特征参数，作为外形研究的变量。

1.1 尾翼弹原始模型参数

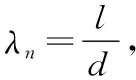
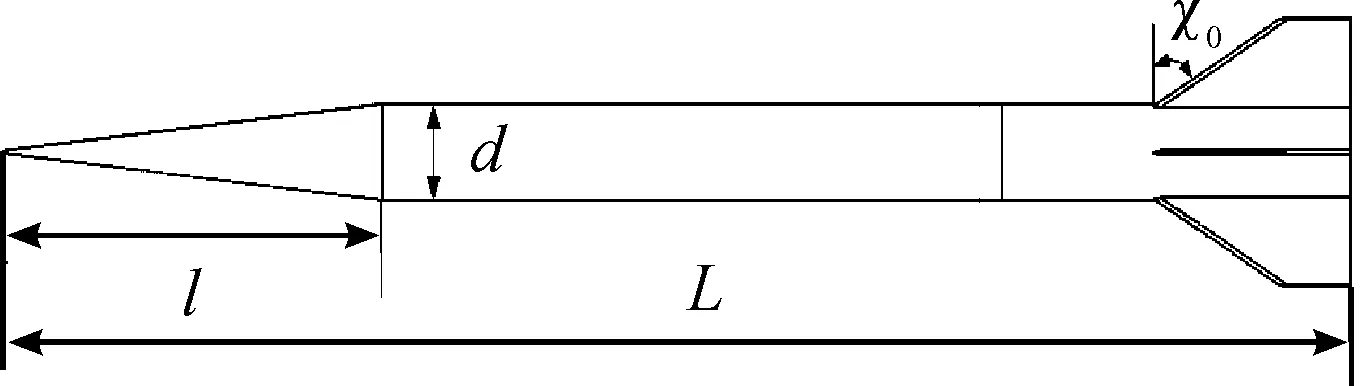
图1 尾翼弹原模型

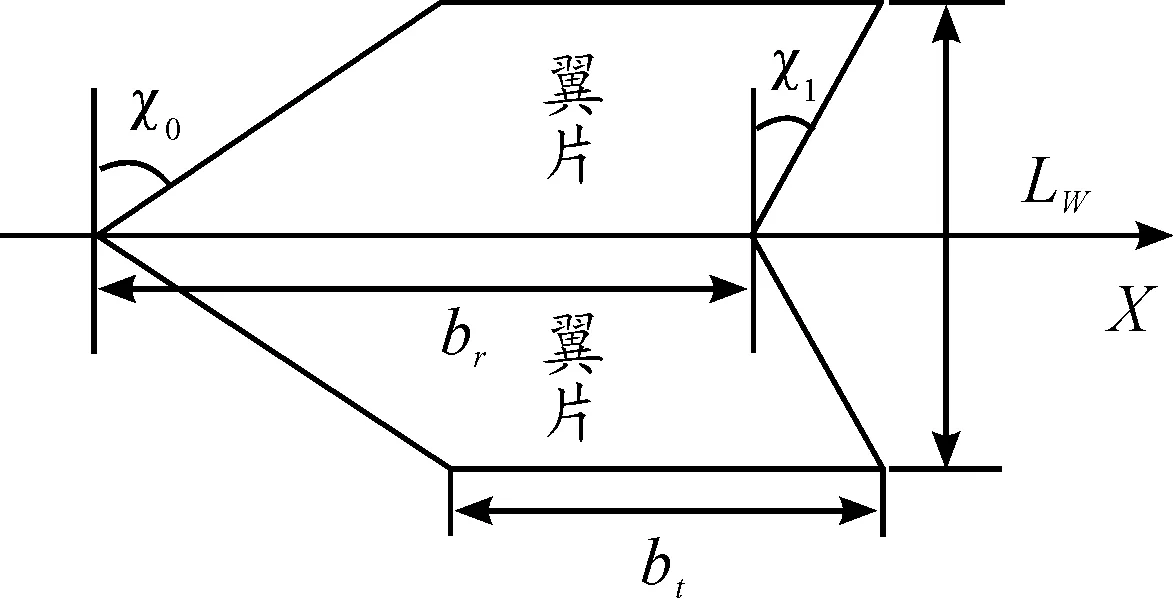
图2 尾翼符号示意图

1.2 尾翼弹不同外形参数

本文所研究的尾翼弹的不同外形尺寸参数，如表1所示。

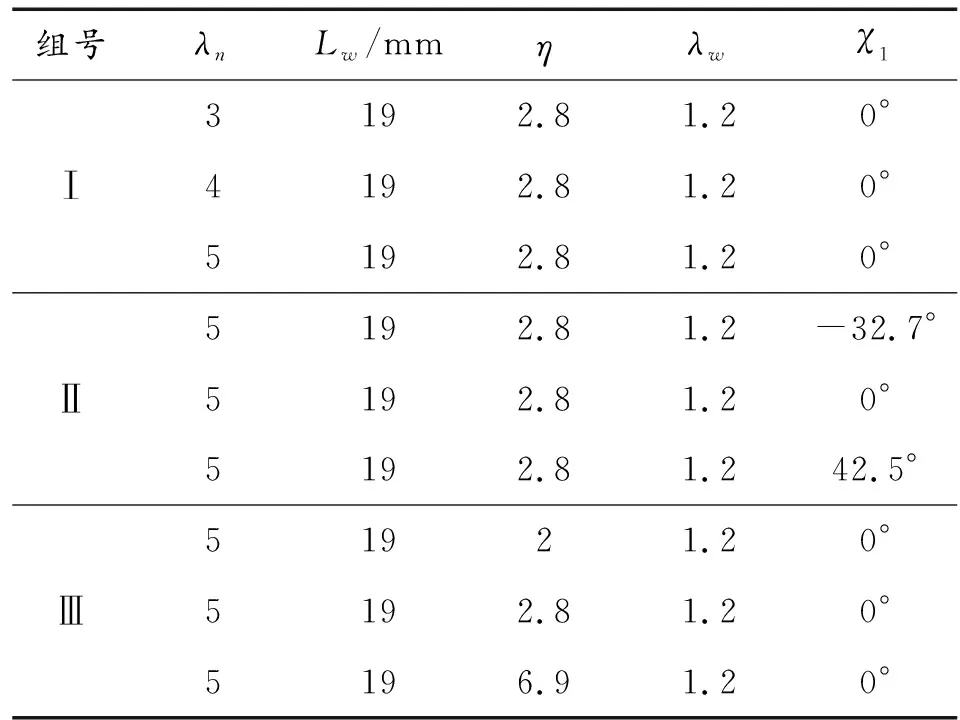
表1 不同外形尺寸参数

2 数值方法

本节介绍计算流体力学中使用到的相关数值方法和过程。

设置气体为理想气体模型，黏度随温度的变化符合萨特兰(Sutherland)公式，忽略体积力和源项，则控制方程为[8]

其中：

Q=[ρ,ρu,ρv,ρw,ρe]T

E=[ρu,ρu2+p,ρuv,ρuw,(ρe+p)u]T

F=[ρv,ρvu,ρv2+p,ρvw,(ρe+p)v]T

G=[ρw,ρwu,ρwv,ρw2+p,(ρe+p)w]T

Ev=[0,τxx,τxy,τxz,βx]T

Fv=[0,τyx,τyy,τyz,βy]T

Gv=[0,τzx,τzy,τyy,βz]T

其中：T为转置符号；ρ为气体密度；u，v，w为速度在笛卡尔坐标系中的3个分量；p为压力；E为单位质量总能。

萨特兰公式为：

其中：μ0为T=288.15 K时的μ值，C为常数，此处C=110.4 K。

湍流模型采用涡黏模型中的SSTk-ω模型，求解2个方程的输运方程，即湍动能k,湍流频率ω，k和ω的输运方程具体形式见文献[9]。SSTk-ω模型能较好的模拟弹箭的气动力，因此选用该湍流模型计算尾翼稳定脱壳穿甲弹的外流场。

综合考虑计算精度与计算效率，将计算域设定为在大的圆柱外流域内再增加一个小圆柱加密区域，大圆柱形外流域直径为18倍弹径长度为10倍弹长[10]，小圆柱流域直径为5倍弹径，长度为3倍弹长,计算域网格如图3所示。求解近壁面区域的方法对气动参数的计算结果有重要影响，因此采用加密网格的方法对黏性子层进行计算，即需要保证y+<5使第一层网格节点位于粘性子层内，并保证边界层数为8，划分得到图4所示的多面体网格。

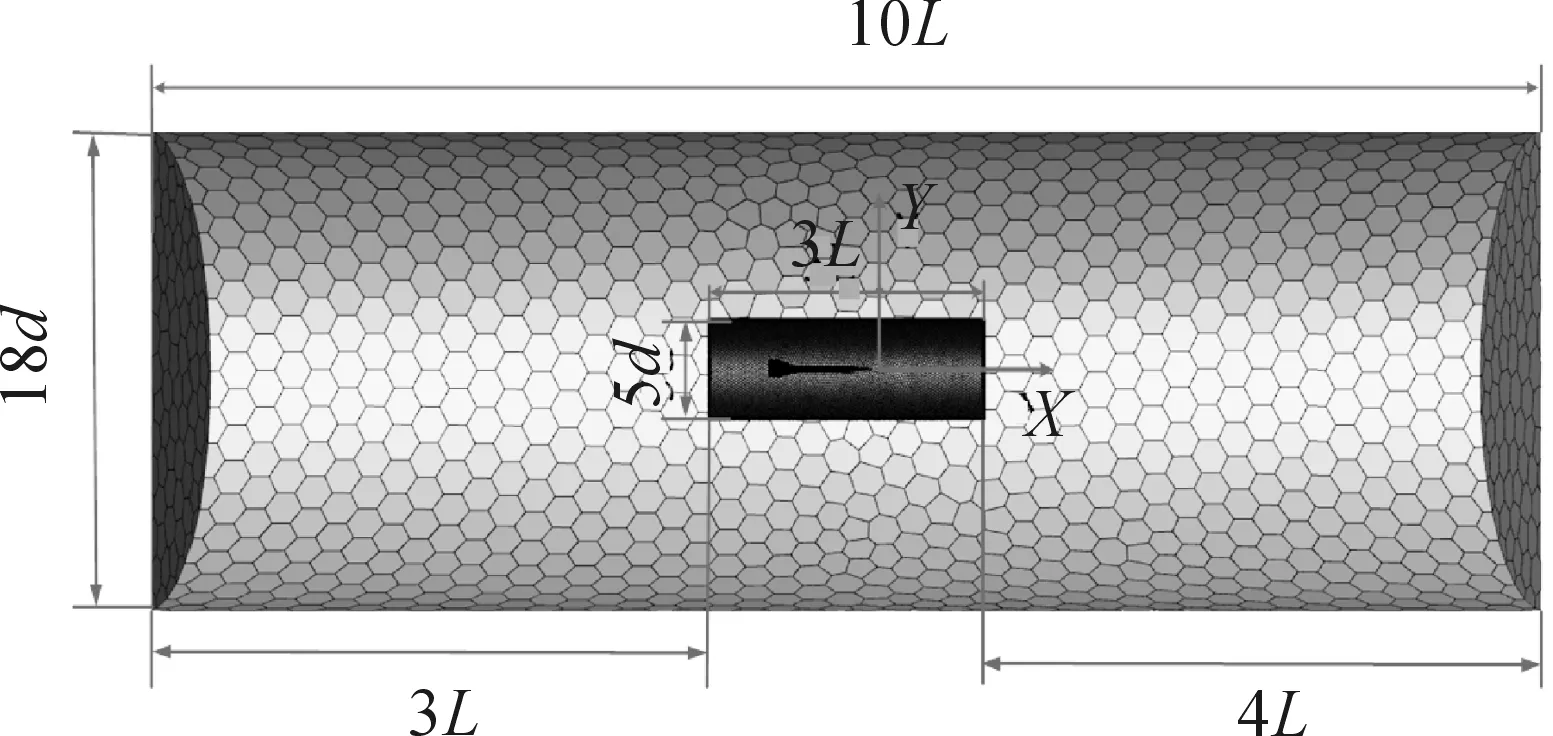
图3 计算域网格

设置流场外壁面为压力远场边界，弹体表面采用无滑移壁面边界条件，求解方法采用压力-速度耦合(Coupled)算法，对流通量采用二阶迎风格式进行离散。

3 计算结果分析

本节将对不同外形的弹体的计算结果进行比较，特别是阻力系数及稳定性。

3.1 原模型气动参数计算

计算来流马赫数为Ma=0.7～3.0；攻角为α=1°～9°的气动参数。得到三音速范围内原模型的气动参数变化曲线，如图5。

由图5(a)可以看出：原模型的阻力系数随着马赫数的增加先急剧增加，而后缓慢减小。这是由于弹箭在亚声速段，弹箭阻力由摩阻和涡阻组成，在跨声速飞行时，弹体表面产生弹体激波，弹箭阻力由摩阻和涡阻，波阻组成，在超声速段飞行时，弹头部脱体激波转变为附体激波，由于激波锥角随着马赫数的增大而减小，激波强度减小，波后压力相应降低，因而波阻减小。由图5(b)(c)可以看到：升力系数，俯仰力矩系数随着攻角近似线性增加而增加，可以采用线性函数或者二次函数进行拟合。

图5 原模型各纵向气动系数的变化曲线

稳定储备量B是指弹药的阻力中心与质心位置的相对距离，即：

其中:α为攻角;h为压心到质心的距离;xp为压心到弹顶的距离;xc为质心到弹顶的距离[11]。对于超音速尾翼弹，其稳定储备量大于15%即可满足飞行稳定性要求[12]。

由图6可以看出：在亚音速范围内,尾翼弹的稳定性随着马赫数的增加而增加，随着攻角的增加也在增加；在超音速范围内，尾翼弹的稳定性随着马赫数的增加减小，随着攻角的增加也在减小，因此只要在高马赫，大攻角下满足稳定性要求，则超音速尾翼弹满足稳定性要求。

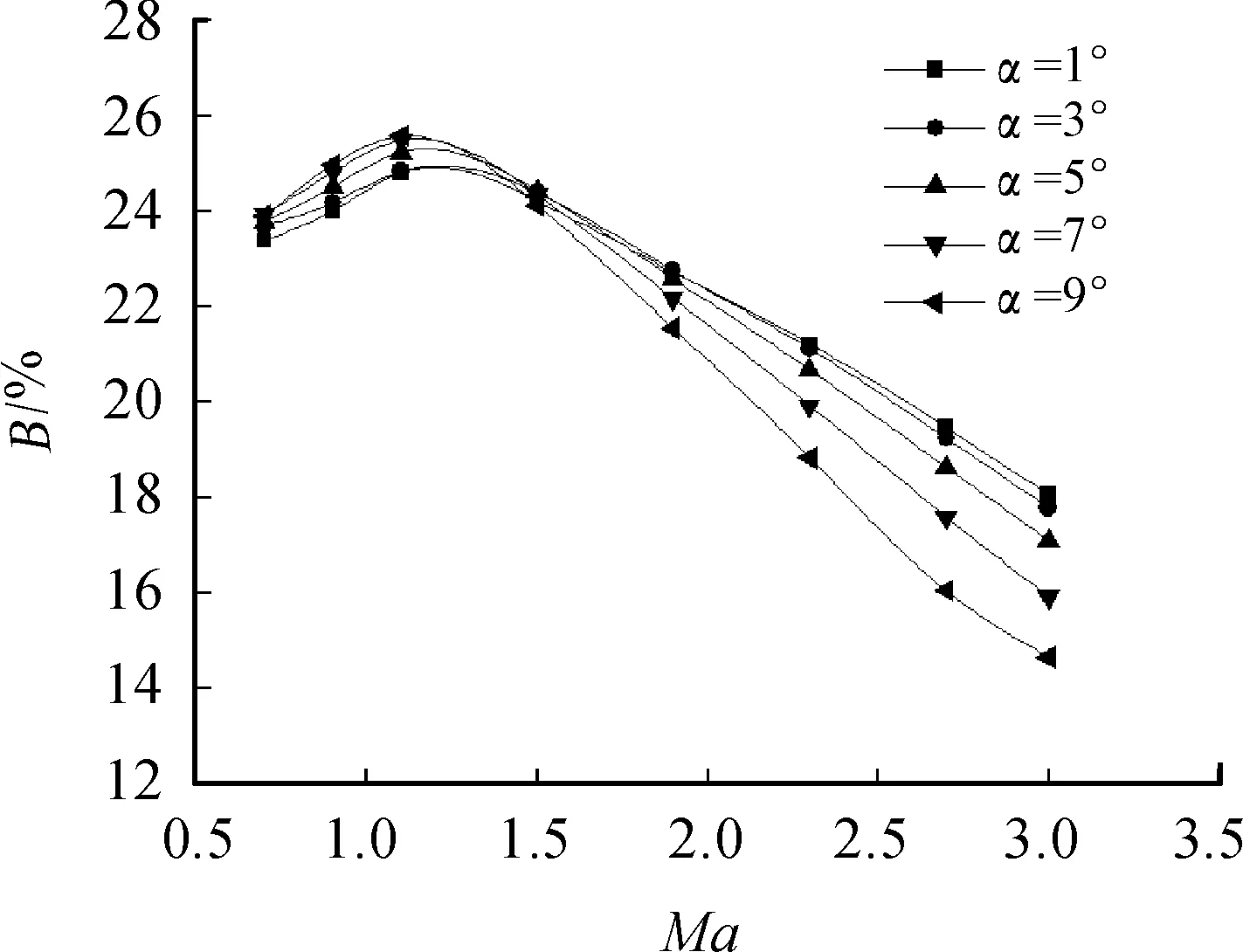
图6 原模型稳定储备量随马赫数的变化曲线

3.2 弹头部长径比的影响

由3.1中得到的尾翼弹稳定储备量的变化律，因此在研究弹头部长径比对尾翼弹阻力系数及稳定性的影响规律时，计算组号Ι对应的弹体模型的气动参数即可。

在弹体其他参数不变，只改变弹丸头部长径比的情况下，由图7可以得出：在超音速范围内，随着弹头部长径比的增加，弹体阻力系数在减小，则弹丸存速增加。因此，增加弹头部长径比，利于提高尾翼弹存速。

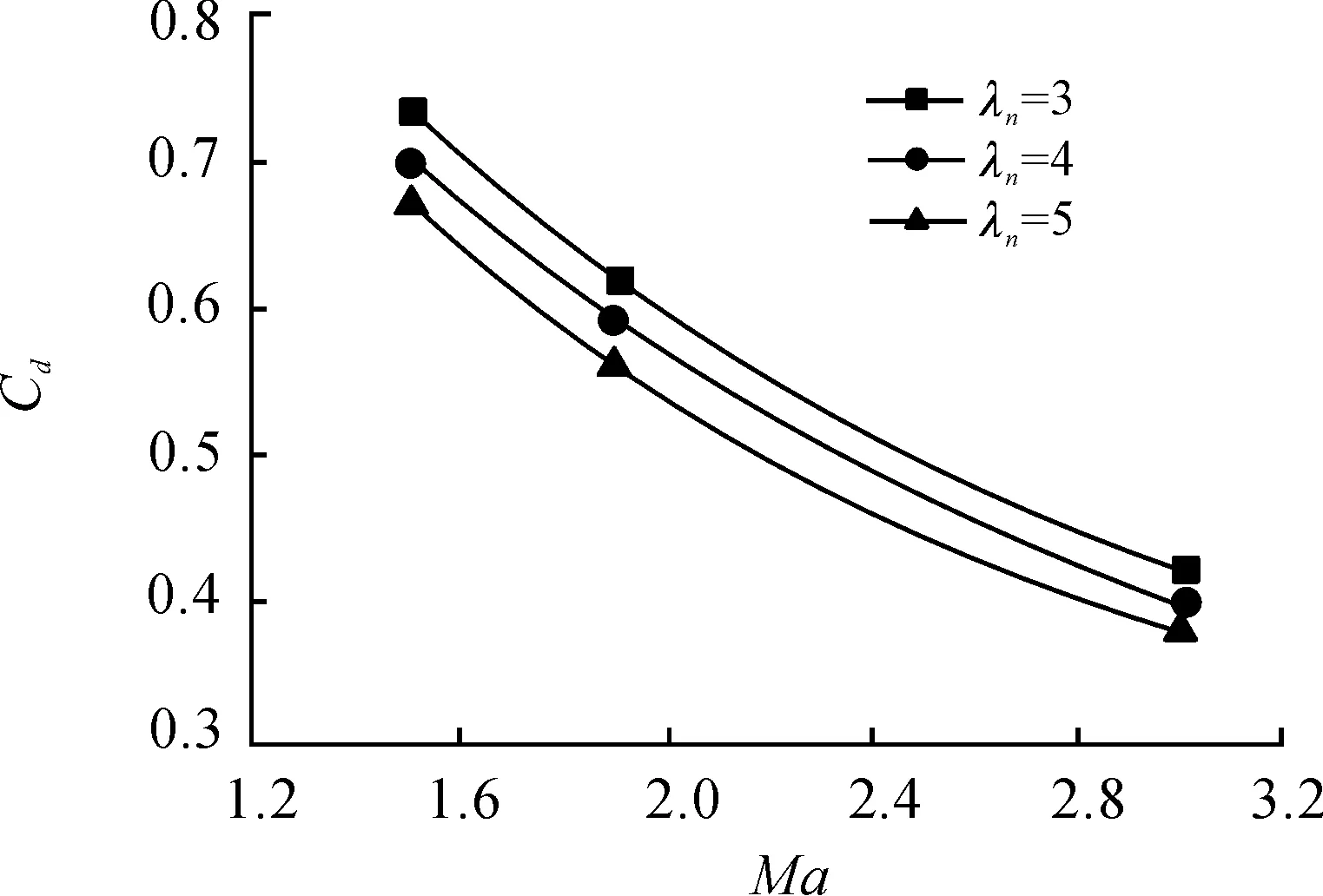
图7 α=0°，阻力系数随马赫数变化曲线

由图8的变化曲线可以得到：尾翼弹的阻力系数，升力系数，俯仰力矩系数都随着弹丸头部长径比的增加而降低。尾翼弹稳定性随着弹头部长径比增加而降低。

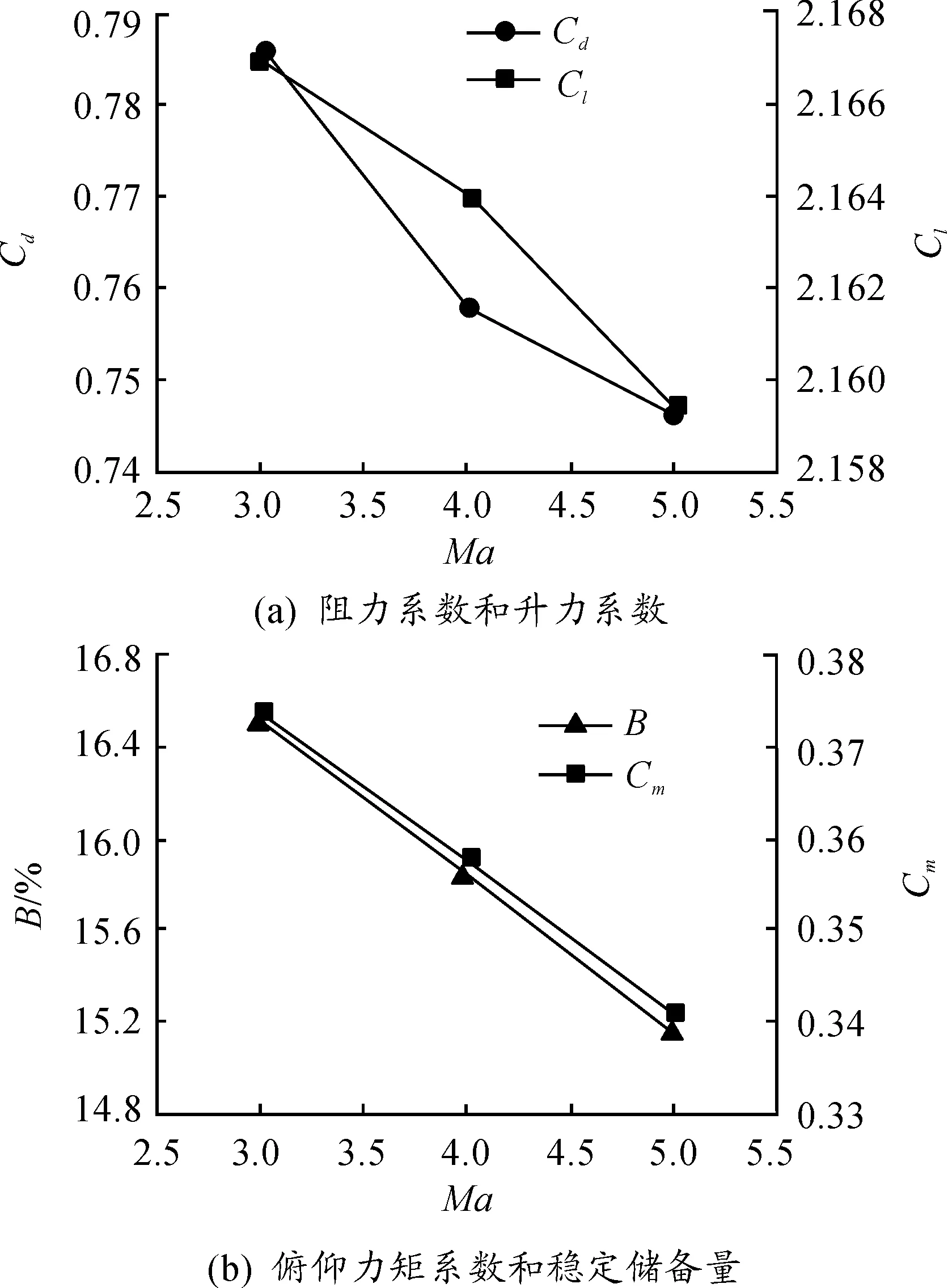
图8 Ma=3.0,α=9°,各气动参数及稳定储备量随头部长径比变化曲线

3.3 尾翼后缘后掠角的影响

在研究尾翼后缘后掠角对尾翼弹阻力系数及稳定性的影响规律时，首先计算组号Ⅱ对应的弹体模型的气动参数。

在弹头部长径比，尾翼根梢比不变，只改变尾翼后缘后掠角的情况下，由图9可以得出：在超音速范围内，随着尾翼后缘后掠角的增加，弹体阻力系数在减小，弹丸存速增加，因此，增加尾翼后缘后掠角，利于提高尾翼弹存速。

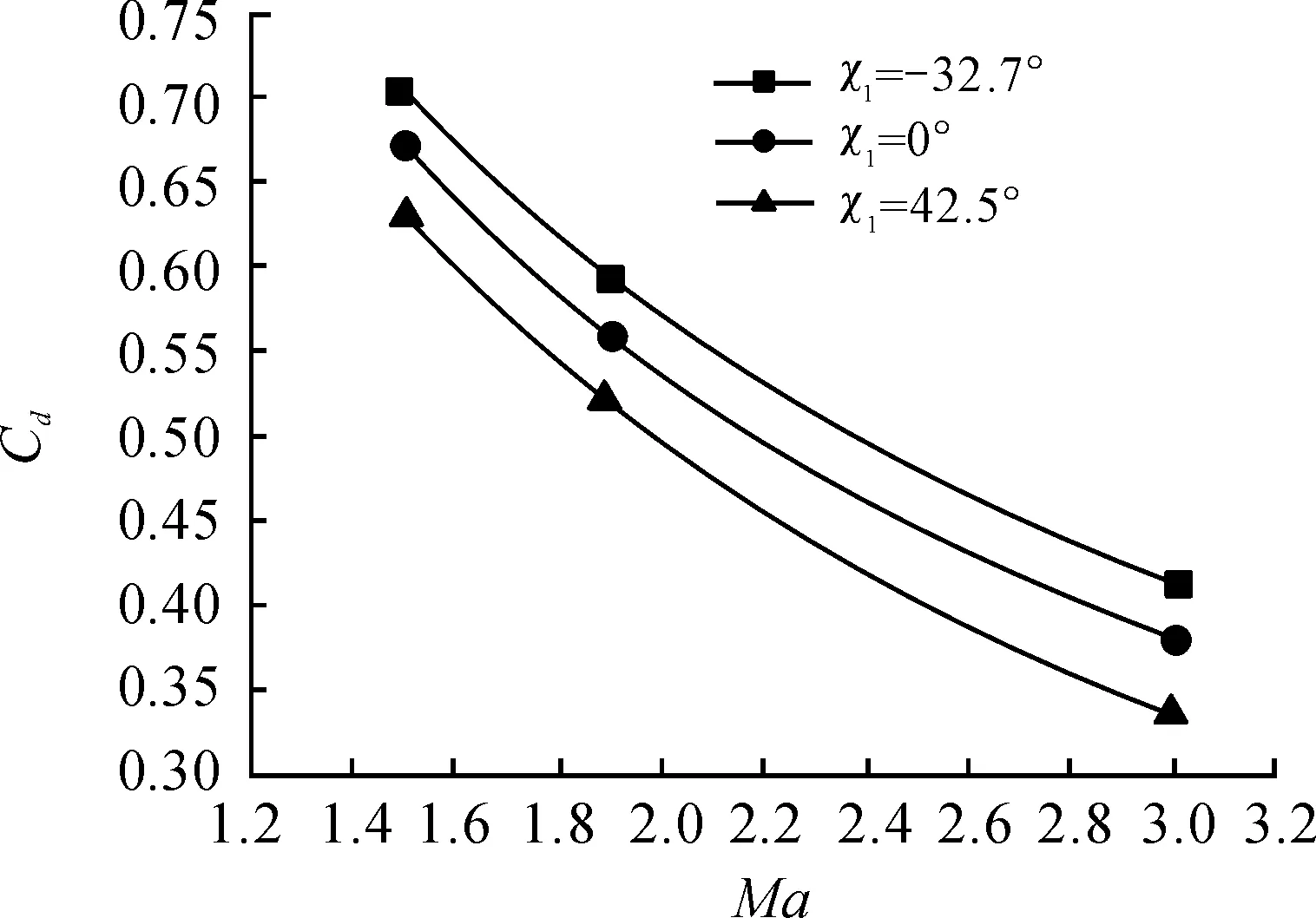
图9 α=0°，阻力系数随马赫数的变化曲线

由图10的变化曲线可以得到，尾翼后缘后掠角由负增加到正时，尾翼弹的阻力系数，升力系数，俯仰力矩系数随着后缘后掠角的增加而减小。尾翼弹稳定性随着后缘后掠角的增加而降低。

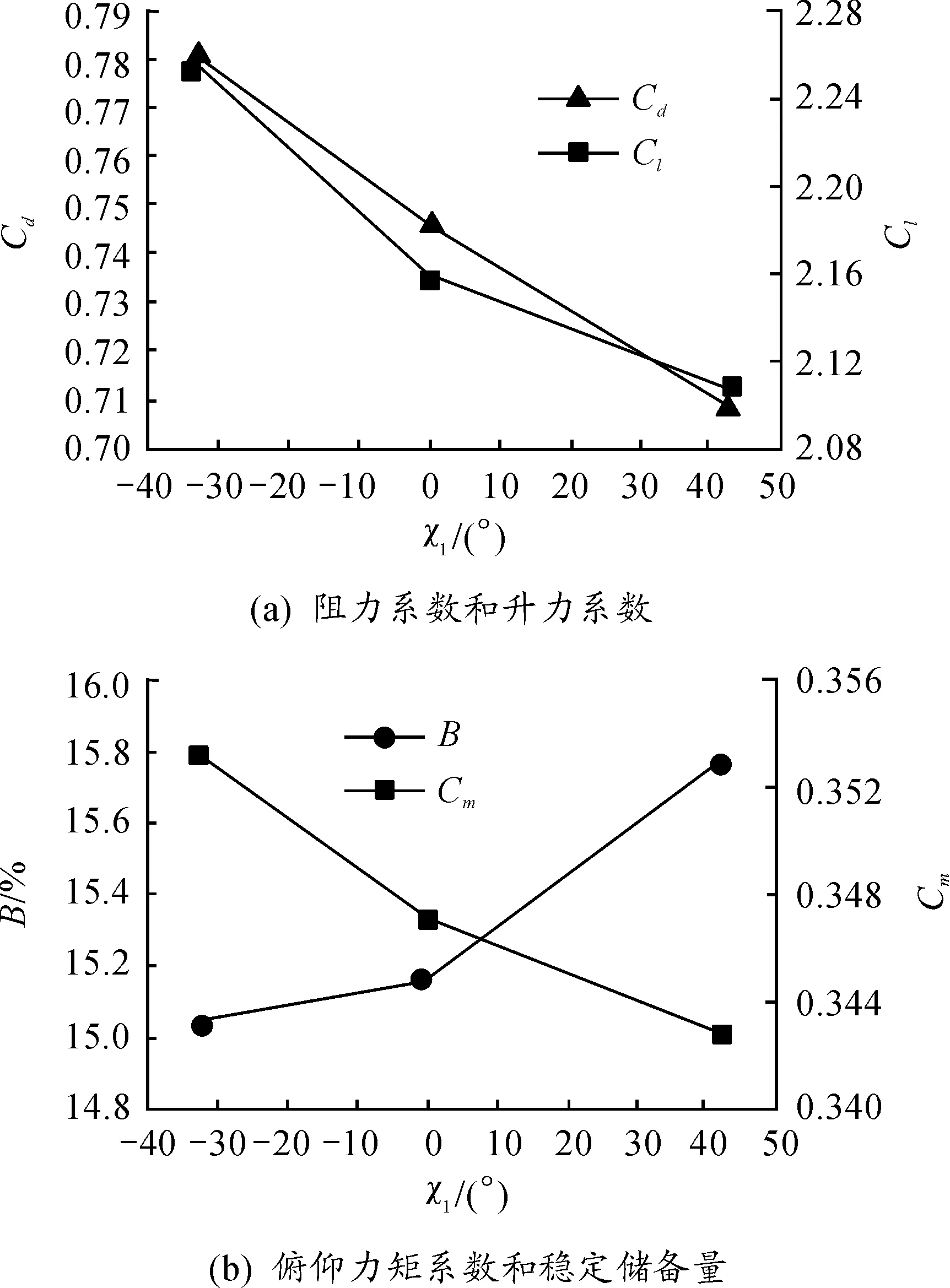
图10 Ma=3.0,α=9°，各气动参数及稳定储备量随尾翼后缘后掠角的变化曲线

3.4 尾翼根梢比的影响

在研究尾翼根梢比对尾翼弹阻力系数及稳定性的影响规律时，首先计算组号Ⅲ对应的弹体模型的气动参数。

在弹头部长径比，后缘后掠角不变，只改变尾翼根梢比的情况下，由图11可以得出：在超音速范围内，随着尾翼根梢比的增加，弹体阻力系数在减小，则弹丸存速增加。因此，增加尾翼根梢比，利于提高尾翼弹存速。

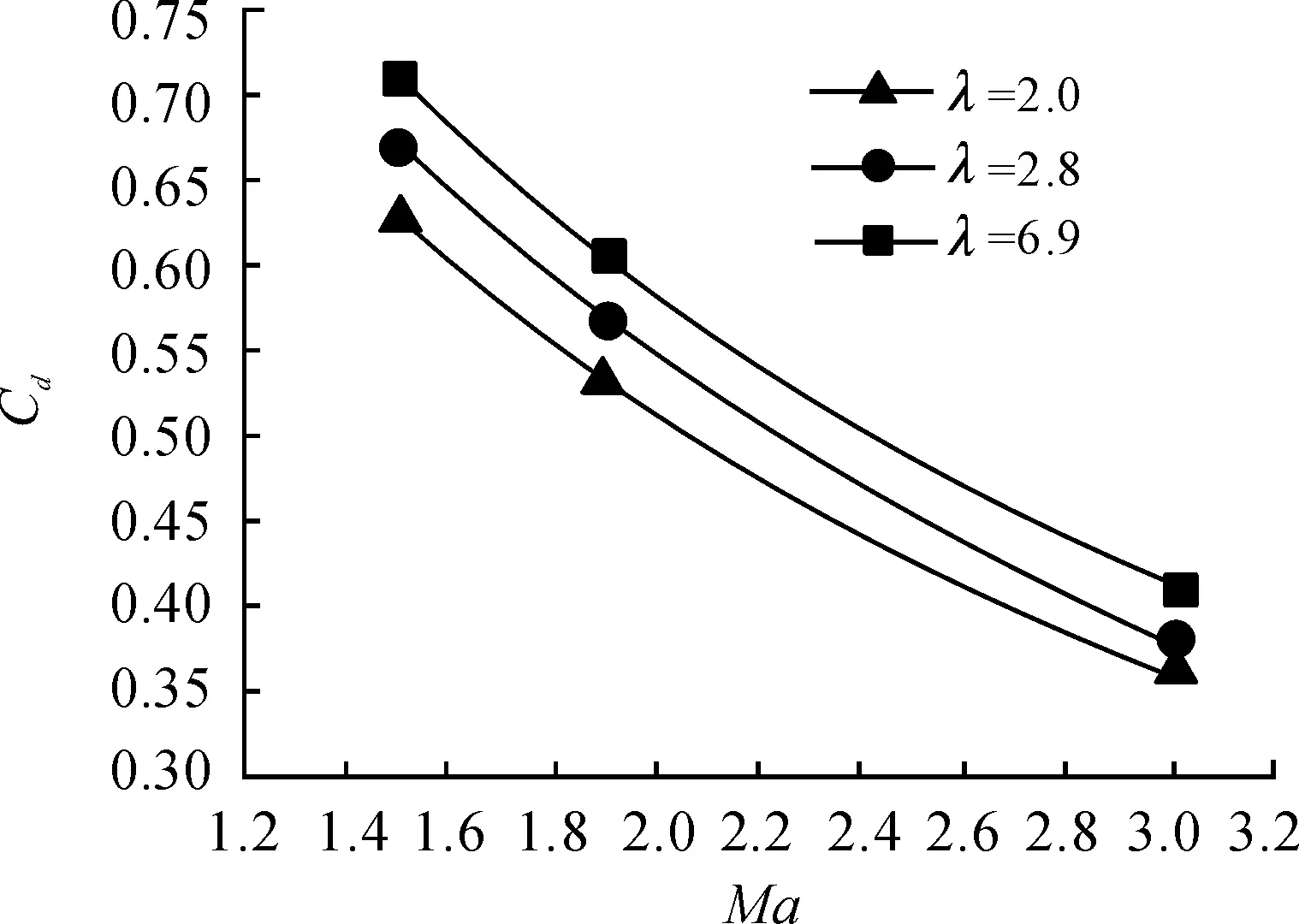
图11 α=0°，阻力系数随马赫数的变化曲线

由图12的变化曲线可以得到，尾翼弹的阻力系数，升力系数，俯仰力矩系数随着尾翼根梢比的增加而降低。尾翼弹稳定性随着尾翼根梢比的增加而降低。

图12 Ma=3.0,α=9°，各气动参数及稳定储备量随根梢比的变化曲线

4 结论

1) 当根梢比及后缘后掠角不变时,增大弹头部长径比,有利于降低弹体阻力系数但稳定性也会随着降低；当根梢比及弹头部长径比不变时，增大后缘后掠角，有利于降低弹体阻力系数并提高弹体稳定性；当后缘后掠角及弹头部长径比不变时，增大前缘后掠角，有利于降低弹体阻力系数但弹体稳定性也会降低。

2) 在超音速范围内,尾翼弹的稳定性随着马赫数的增加而减小，随着攻角的增加也在减小。因此可以用在高马赫数，大攻角下的稳定储备量来判断超音速尾翼弹的稳定性。

可以在本文的研究基础上，对尾翼稳定脱壳穿甲弹的外形参数进行优化设计。