转管炮机心结构参数化分析

原 平，戴劲松，王茂森

(南京理工大学 机械工程学院， 南京 210000)

转管炮机心组在星形体导轨和炮箱凸轮曲线槽的共同作用下做循环往复运动，完成射击循环动作。不同炮管数量的转管炮射速可达1 500～10 000发/min，机心组自动循环时间短，运动状态变化剧烈。在某型转管炮射击实验中，发现机心组运动卡滞，机心滚轮与炮箱凸轮曲线槽之间以及机心与星形体导轨之间的磨损较严重。关于减少机心滚轮与炮箱凸轮曲线槽之间的正压力、降低驱动功耗方面，前人研究的重点在于对炮箱凸轮曲线槽的优化设计上。文献[1-2]通过对炮箱凸轮曲线槽过渡段进行优化设计，使得机心滚轮与凸轮曲线槽间的接触力降低。文献[3]研究了机心主滚轮在机体上的布局对机心滚轮和炮箱凸轮曲线槽之间接触力的影响。文献[4]主要对星形体导轨倾角进行了研究，而对机心结构没有进行较为细致的研究。为了解决上述实验中出现的问题，展开对转管炮机心结构的研究，根据达朗贝尔原理[5]，列出机心受力的动平衡方程，应用Matlab编程分析机心结构参数的变化与机心滚轮和炮箱凸轮曲线槽正压力之间的关系。

1 动力学分析

1.1 机心运动过程分析

机心组在转管炮凸轮曲线槽约束下做循环往复运动，运动特性取决于转管炮凸轮曲线槽的特征。根据转管炮循环图，转管炮凸轮曲线槽分段设计[6]，凸轮槽展开如图1所示。在一个射击循环中，θ1为输弹加速段，θ2为输弹等速段，θ3为输弹减速段，θ4为击发过程直线段，θ5为退壳加速段，θ6为退壳等速段，θ7为退壳减速段，θ8为进出弹直线段。所以在一个射击循环，机心组经历两次直线段，两次加速段，两次减速段、两次等速段[7]。取机心组其中一个机心为研究对象，不考虑弹丸的情况下，分析各个过程机心的动力学。

图1 凸轮槽展开示意图

1.2 机心动力学分析

1) 机心加速段动力学分析

机心滚轮与凸轮曲线槽加速段受力分析可得，凸轮曲线槽对滚轮的正压力为N，方向垂直于凸轮曲线槽接触面，机心滚轮按纯滚动处理，所受到的摩擦力为f1N，方向沿凸轮曲线槽切线方向，与运动方向相反。f1为滚动摩擦系数。将正压力和摩擦力投影，分解为沿着机心轴向运动方向的主动推力Nx和垂直于运动方向横向力Ny，其中α为压力角：

(1)

其中令：

(2)

机心的主要设计结构参数以及加速段受力分析如图2所示，O点为机心中心，在身管轴线延长线上，B点为机心滚轮理想受力点，A点为导轨对机心侧向正压力N1作用延长线与O、B连线的交点，D、D′点为导轨对机心作用中心点。令A点和B点连线长度为h0，O点和B点连线长度为h，O点与D，D′连线的垂直距离为h1，h1在O点以下为负值，在O点以上取正值。A点和D点连线长度为L0，C为D，D′连线长度，L为机心纵向长度，θ为星形体导轨倾角。当转管炮凸轮曲线槽和身管组中心圆给定之后，h等于机心滚轮公转半径减去身管组中心圆半径。机心纵向长度L取决于凸轮的轴向长度，研究机心结构参数影响就集中在星形体导轨倾角θ、机心径向宽度C、导轨理想作用点高度h1上。

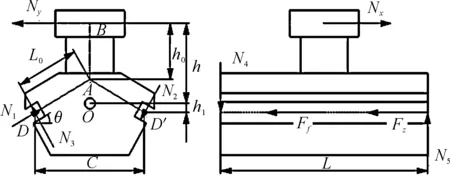
图2 机心受力分析示意图

由几何关系可得：

(3)

机心加速段受力分析可得，在机心主视图上，机心受到星形体导轨正压力N1、N2、N3，作用点和方向如图上所示。根据受力列出机心主视图的力平衡方程：

(4)

在机心左视图上，机心受到星形体导轨正压力N4、N5，作用点和方向如图上所示。图中Ff为星形体导轨对机心正压力以及由机心离心力和切向惯性力引起的摩擦力，f2为星形体导轨与机心之间的摩擦系数，m为机心质量，r为身管组中心圆半径，ω为星形体转动角速度，ε为星形体转动角加速度。

(5)

在机心加速度反方向施加达朗伯力Fz得到机心左视图动平衡方程：

(6)

由式(1)～(6)联立可得在机心加速段运动中凸轮曲线槽对滚轮的正压力N：

(7)

其中：

(8)

2) 机心减速段动力学分析

机心在减速段运动时，凸轮曲线槽对滚轮的正压力N与机心轴向运动方向相反，受力分析计算可得，只需将f1变为-f1，f2变为-f2即可得到在机心减速段运动中凸轮曲线槽对滚轮的正压力N：

(9)

其中μ，λ同上。

3) 机心等速段动力学分析

机心运动到等速段时，机心加速度为0，这时机心等速段运动中凸轮曲线槽对滚轮的正压力N为：

(10)

其中μ，λ同上。

4) 机心直线段动力学分析

机心运动到直线段时，机心轴向位移为0，这时机心直线段运动中凸轮曲线槽对滚轮的正压力N为0。

2 实例分析

2.1 参数化计算

以某型转管炮为例，其炮箱凸轮曲线槽是按照摆线修正梯形加速度运动规律设计，摆线修正梯形加速度运动规律的类加速度曲线没有突变现象，因此从动件没有刚性和柔性冲击[8-10]。位移和压力角曲线如图3。

身管组中心圆半径r=50 mm，机心滚轮公转半径r1=78 mm。机心的结构参数：机心中心O到机心滚轮理想受力点A的距离h=28 mm，机心纵向长度L=80 mm，星形体导轨倾角θ∈[0°,45°]、机心径向宽度C∈[35,50]，导轨理想作用点高度h1∈[-8,8]，机心质量m根据具体的结构尺寸计算得到。凸轮曲线槽与机心滚轮之间的滚动摩擦系数f1的取值根据机械手册[11]：f=μg/R，μg为滚动摩擦力臂，钢与钢的滚动摩擦力臂一般取值为0.2～0.4，R为滚动摩擦半径，实例中的机心滚轮半径R=12.5 mm，得到f1=0.03。机心与星形体导轨之间的滑动摩擦系数取f2=0.1。这里只研究转管自动机稳定工作的情况，星形体角加速度ε=0。加速度a和压力角α根据凸轮曲线方程计算得到。

图3 凸轮曲线槽位移和压力角曲线

当射速为4 000发/min时，计算得到对应的角速度ω=104.72 rad/s。应用Matlab中的surf函数，带入数据得到C、h1、θ结构参数的变化对机心滚轮与凸轮曲线槽之间的正压力最大值的变化情况，X坐标为C，Y坐标为h1，Z坐标为Nmax，如图4所示。当分别取C、h1等于其取值范围最大最小值，研究随着θ的变化，正压力最大值的变化情况，如图5所示。当C，h1分别取最小与大值时，Nmax随ω变化情况，如图6所示。

图4 不同倾角θ，Nmax随C、h1变化情况

2.2 计算结果分析

从图4可以看出，当星形体导轨倾角一定时，随着机心径向宽度C以及导轨理想作用点高度h1的增大，机心滚轮与凸轮曲线槽之间的正压力最大值成规律性变化，其最大值逐渐减小。正压力Nmax的最大值位于C=35 mm，h1=-8 mm处，即C、h1取得其取值范围的最小值时。正压力Nmax的最小值位于C=50 mm，h1=8 mm处，即C、h1取得其取值范围的最大值。

由图5可以看出，当机心径向宽度C以及导轨理想作用点高度h1分别取最小与最大值时，Nmax随θ变化情况。θ从0°到45°变化中，C、h1取最大值时，可以看出Nmax先增大后减小，Nmax最小等于4 315.2 N，此时导轨倾角θ=0°。当C、h1取最大值时，Nmax随着θ的增大而逐渐减小，Nmax最小等于3 154.7 N，此时导轨倾角θ=45°。正压力减小幅度26.9%。可以得出要使机心滚轮与凸轮曲线槽之间的正压力减小，应选取较大的机心径向宽度C以及导轨理想作用点高度h1。

图5 C、h1取最小值与最大值时，Nmax随θ变化情况

图6 当C、h1取最小与大值时，Nmax随ω变化情况

由图6可以看出，当机心径向宽度C以及导轨理想作用点高度h1分别取最小与最大值时，Nmax随ω变化情况。随着转管炮射速的提高，角速度增大，Nmax增长速度由慢变快，倾角变化对Nmax的影响也越来越大。当C、h1取最大值时，星形体导轨倾角45°的Nmax小于导轨倾角0°的Nmax，当C、h1取最小值时，星形体导轨倾角45°的Nmax大于导轨倾角0°的Nmax。得出当机心选取较大的径向尺寸和导轨理想作用点高度时，导轨倾角越大越好，反之，水平最好。

由以上分析，取C=50 mm，h1=8 mm，θ=45°，机心滚轮与凸轮曲线槽之间的正压力最小，星形体旋转一周，机心滚轮与凸轮槽正压力变化曲线如图7之实线，图7之虚线为原设计C=40 mm，h1=-5 mm，θ=30°的机心滚轮与凸轮槽正压力变化曲线。原机心模型Nmax=4 065.9 N，新机心模型Nmax=3 154.7 N，最大减小幅度为22.4%。

图7 原模型与新模型正压力曲线

3 结论

在对某转管炮进行动力学分析的基础上，通过参数化分析，得到了机心结构参数的改变对机心滚轮与转管炮凸轮曲线槽的正压力的变化规律。为了得到较小的正压力，减小驱动功耗，机心与导轨接触的径向宽度应尽量选较大的尺寸，导轨对机心作用中心点应位于机心中心以上，距离机心中心点越远，正压力越小。当机心选取较大的径向尺寸和导轨理想作用点高度时，导轨倾角越大越好，反之，水平最好。