基于三点定位与加权坐标的三角定位算法

徐 乐，韦玉科

广东工业大学 计算机学院，广州510006

1 引言

由于人类大部分时间都在室内活动，所以室内定位技术的研究变得更加重要。而在室内定位技术的研究中，室内定位算法的选择将会直接影响定位结果的精准度。

目前，室内定位算法[1]主要分为基于测距和非测距两种。典型的基于测距定位算法有：基于接收信强度指标RSSI[2]、基于到达时间TOA[3]、基于到达角度[4]、基于到达时间差TDOA[5]等。典型的基于非测距定位算法有：Amorphous 算法[6]、质心算法[7]。而基于测距定位算法较于基于非测距定位算法，具有更高的定位精度。其中，基于RSSI测距定位算法[8]由于开销最小而被广泛应用于室内定位系统。

基于RSSI 测距定位算法是利用节点从定位点接收到的功率，并通过功率距离转换和定位算法，推算出定位点的位置。因此，对于基于RSSI 测距定位算法的改进方向主要为：降低RSSI数据集的不稳定性，提高RSSI测距模型的准确性和提高定位算法的精度。文献[9]提出了一种基于多属性代价函数的WiFi 与蓝牙TLS 融合定位算法，该算法以多属性代价函数评估信标的定位能力，同时利用TLS对待定位节点进行最优位置估计。文献[10]提出一种基于特征匹配和距离加权的蓝牙定位算法，该算法在离线状态生成指纹数据库，在在线状态根据排序特征向量完全匹配算法、排序特征向量最相似匹配算法和基于距离的最优加权KNN 定位算法实现定位。但是该算法在实际操作时需要采集大量指纹点，工作量较大。文献[11]提出一种基于蓝牙RSSI 的贝叶斯区域判别定位算法，该算法接收信号强度划分区域并对区域内进行定位，但是该算法运算较为复杂。文献[12]提出基于RSSI 测距校正的拟牛顿定位算法，该算法通过引用高斯函数对RSSI 值进行筛选和对剩余的RSSI 数据进行加权操作，来获取最优的RSSI 数据，后采用最小二乘法估计和拟牛顿法迭代来确定目标结点的位置。

现有的基于RSSI 测距定位算法的改进算法[13]虽然提高了定位结果的精确度，但是算法过程都过于复杂。因此，本文提出一种基于三点定位与加权坐标的三角定位算法。该算法在RSSI测距阶段通过多次测量获取适合的RSSI-距离模型，同时针对RSSI 值波动性大的缺点，对同一定位目标的RSSI 数据集进行卡尔曼滤波操作。本文的定位算法将三点定位与三角定位算法结合。首先经过基于RSSI 选取的三点定位算法获取三个粗定位结果坐标；然后给这三个定位坐标赋予相应的权值得到加权坐标；最后通过三角定位运算得到最终定位坐标结果。实验结果表明，本文提出的算法在实际应用中能有效地降低定位误差。

2 RSSI 测距原理与RSSI数据处理

2.1 RSSI测距原理

RSSI 测距原理是基于渐变模型的[14]，即随着距离的增加信号强度有规律的衰减。在进行定位时，根据接收信号强度、发射信号强度、接收端和发射端之间的距离构建信号强度-距离衰减模型，将测量过程中获取的RSSI 数据集转换为到待定位点的距离数据集，用于计算待定位点的位置。

已知无线信号的发射功率与接收功率之间的关系如方程式（1）所示：

其中，RSSI 为无线信号的接收功率，P 为无线信号的发射功率，d 为接收端与发射端之间的距离，n为环境衰减因子，大小由无线信号传播环境决定。

对方程式（1）两端进行取对数操作并化简，得到方程式（2）：

因为发射功率是已知，所以接收端信号强度RSSI与传输距离d 之间的关系可用方程式（3）表示：

其中，n表示环境衰减因子，A表示发射端与接收端相隔1 m时的信号强度。在实验环境中，通过大量测试，得出实验环境下的RSSI-距离衰减模型。如图1 所示，根据RSSI 原始数据与衰减模型计算结果对比可知，在RSSI原始数据与衰减模型计算结果之间的相似拟合度为96%的条件下，A=-87.074 0，10n=-8.6，所以RSSI-距离衰减模型公式如方程式（4）所示：

图1 信号衰减模型测试结果图

由图1 可知，RSSI-距离衰减模型中，原始数据与拟合数据之间相似度很高，同时模型近似服从对数分布模型。

2.2 卡尔曼滤波

在实际测试场景中，RSSI 数据易受到各种干扰噪声的影响，同时无线信号受到多径反射传播、非视距等影响，这些影响会使获取到的RSSI 数据存在着很大的波动性和误差。为了使获取到的RSSI 数据的波动性和误差降低，同时为了提高定位精度，本文在进行定位运算之前对获取到的RSSI 数据先进行滤波处理。文献[15]中对几种不同数据滤波方法的效果进行了比较，其中卡尔曼滤波算法的效果相对较好。

卡尔曼滤波算法是以最小均方误差作为估计的最佳准则来寻求一套递推估计的算法。其基本思想是：采用信号与噪声的状态空间模型，利用前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计，求出当前时刻的估计值。当对象模型足够准确且系统状态和参数不发生突变时，性能较好。且该方法操作简单，数据存贮量小，具有很强的实时性。同时，卡尔曼滤波算法能在一定程度上削弱由于噪声叠加造成的RSSI 观测值偏离，经过卡尔曼滤波算法处理后的RSSI值，具有更好的稳定性。

本文采用卡尔曼滤波方法对获取的RSSI 数据进行处理，以达到降低RSSI 值波动性和减少RSSI 值误差的目的。对获取的RSSI 数据进行卡尔曼滤波前后的效果图如图2所示。

图2 RSSI数据滤波前后效果图

由图2可看出，卡尔曼滤波后的RSSI数据的波动性变小了，说明卡尔曼滤波对提高基于RSSI 测距定位算法的稳定性和准确性有一定的效果。

3 改进的三角定位算法

3.1 三角定位算法

三角定位算法[16]是RSSI 测距定位算法中常用的定位算法之一。三角定位算法原理是对平面上的三个已知位置的点和未知位置的目标点，测出已知点到目标点的距离，以已知点为圆心，到目标点的距离为半径画出相交的三个圆，三圆的相交点即为目标点的位置。如图3所示。

图3 三角定位算法原理图

由RSSI-距离衰减模型可知RSSI 转换为距离公式如方程式（5）所示：

假设在一个平面区域内，安放了三个蓝牙Beacon节 点 分 别 为A(x1,y1)、B(x2,y2)、C(x3,y3)，待 定 位 终 端D(x,y)，RSSIA、RSSIB、RSSIC为接收到A、B、C 三点的信号强度值，根据方程式（5）可求得A、B、C 到D 的距离为d1、d2、d3。故三角定位算法的表达式可用方程式（6）表示：

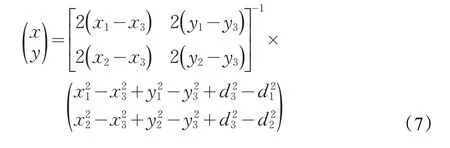
3.2 改进的三角定位算法

在实际场景中，由于无线信号传播易受干扰，获取到的RSSI值存在着波动性，通过RSSI-距离衰减模型求得的距离与实际距离具有一定的误差，导致三圆相交出现多个交点，所以通过三角定位运算得出的定位结果存在着误差。因此，本文提出一种基于三点定位与加权坐标的三角定位算法，该算法将三点定位与三角定位算法相结合。首先分别通过三种不同的基于RSSI选取方式的三点定位算法得到三个粗定位结果坐标；然后给这三个定位结果坐标赋予相应的权值得到加权坐标；最后加权坐标经过三角定位运算得到待定位目标点坐标。

3.2.1 基于RSSI选取的三点定位算法

基于RSSI 选取的三点定位算法主要是利用不同的选取方式获得三个蓝牙Beacon 节点，通过三点定位算法得到粗定位结果。本文所用的RSSI选取方式可分为基于功率的、基于距离的和基于功率与距离结合的三种。下面分别介绍这三种选取方式。

（1）基于功率的RSSI选取方式

基于功率的RSSI 选取方式主要是选取获取的数据包中RSSI值最大的三个蓝牙Beacon节点。其具体步骤如下：

步骤1 获取所有蓝牙Beacon节点数据包中的RSSI数 据 集 合RSSI={RSSI1,RSSI2, …,RSSIn}，n 为 蓝 牙Beacon节点个数。

步骤2 选取RSSI集合中值最大的三个蓝牙Beacon节点，并获取相应的X，Y 轴坐标值集合X={x1,x2,x3}和Y={y1,y2,y3}。

（2）基于距离的RSSI选取方式

基于距离的RSSI 选取方式主要是选取经过RSSI-距离转换后的距离数据集中最小的三个蓝牙Beacon 节距离转换后的距离数据集中最小的三个蓝牙Beacon 节点。其具体步骤如下：

步骤1 根据方程式（5），对获取的所有蓝牙Beacon节点数据包中的RSSI值进行RSSI-距离转换，得到距离集合d={d1,d2,…,dn}，n为蓝牙Beacon节点个数。

步骤2 选取距离集合d={d1,d2,…,dn}中距离值最小的三个点

步骤3 获取对应的蓝牙Beacon节点的X，Y 轴坐标值集合X={x1,x2,x3}和Y={y1,y2,y3}。

（3）基于功率与距离结合的RSSI选取方式

基于功率与距离结合的RSSI 选取方式主要是选取获取的数据包中RSSI 值最大的蓝牙Beacon 节点，和距离该节点的距离值最小的两个蓝牙Beacon 节点。其具体步骤如下：

步骤1 获取所有蓝牙Beacon节点数据包中的RSSI数 据 集 合RSSI={RSSI1,RSSI2,…,RSSIn}，n 为 蓝 牙Beacon 节点个数，选取RSSI 集合中最大的一个蓝牙Beacon节点RSSImax。

步骤2 计算除RSSImax之外的所有蓝牙Beacon 节点 到 RSSImax的 距 离 ，并 得 到 距 离 集 合d={d1,d2,…,dm-1}，m 为蓝牙Beacon节点个数。

步骤3 选取d={d1,d2,…,dm-1}中值最小的两个点，获取RSSImax和对应的蓝牙Beacon 节点X，Y 轴坐标值集合X={x1,x2,x3}和Y={y1,y2,y3}。

通过上述的选取方式中的任意一种方式均可获取到需要的三个蓝牙Beacon 节点X，Y 轴坐标值集合X={x1,x2,x3}和Y={y1,y2,y3}，通过方程式（8）可得到粗定位结果坐标。

其中，p、q、t 为权值。

方程式（8）中的权值p、q、t 是根据选取的三个蓝牙Beacon 节点数据包中的RSSI 值之间差距的大小来设置的。具体权值的设置过程可以用伪代码描述，如下所示。

描述：方程式（8）中权值的设置

输入：RSSI={rssi1,rssi2,rssi3}

X={x1,x2,x3}

Y={y1,y2,y3}

输出：(x,y)

算法过程：

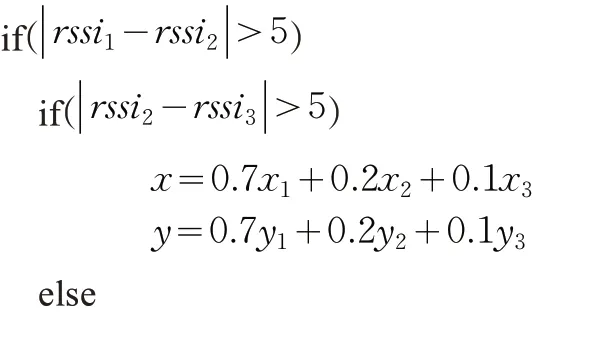
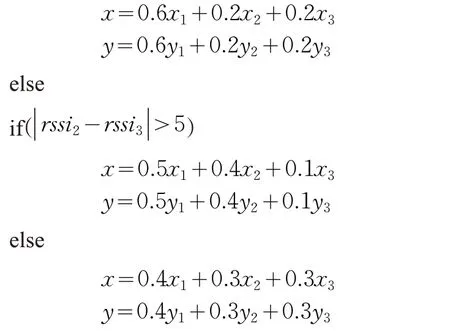
针对方程式（8）的权值的设定是经过大量测试后确定的。

3.2.2 基于加权坐标的三角定位算法

基于加权坐标的三角定位算法主要是对经过基于RSSI 选取的三点定位算法后的三个定位结果坐标赋予不同的权值，然后通过三角定位运算得到待定位点坐标。其具体步骤如下：

步骤1 经过基于RSSI 选取的三点定位算法，得到三个粗定位结果坐标A(x1,y1),B(x2,y2)和C(x3,y3)。

步骤2 根据方程式（9），给A，B，C 坐标赋予相应的权值，得到加权坐标和

其中，α、β、γ为权值。

步骤3 根据方程式（5）计算A、B、C 对应的蓝牙Beacon节点到待定位目标的距离。

步骤4 根据方式（10）可得到待定位点的坐标(x,y)。

在基于坐标加权的三角定位算法中，坐标加权流程如图4所示。

图4 坐标加权流程图

3.2.3 基于三点定位与加权坐标的三角定位算法

基于三点定位与加权坐标的三角定位算法先对待定位点进行三点定位运算，得到三个粗定位结果坐标，然后对这三个粗定位结果坐标进行加权操作，得到加权坐标，最后将这三个加权坐标经过三角定位运算得到待定位点坐标。

基于三点定位与加权坐标的三角定位算法的流程如图5所示。

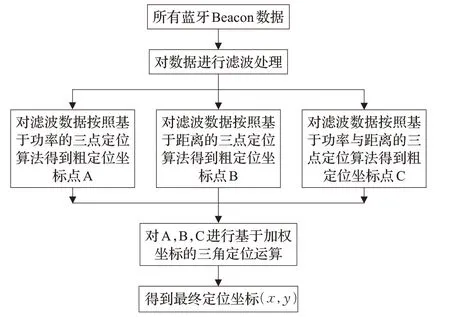
图5 基于三点定位与加权坐标的三角定位算法流程图

基于三点定位与加权坐标的三角定位算法的具体步骤如下：

步骤1 获取所有蓝牙Beacon节点数据包。

步骤2 对获取的数据中的RSSI数据进行卡尔曼滤波处理，得到处理后的新RSSI数据RSSIK。

步骤3 对RSSIK分别进行三种不同的基于RSSI选取的三点定位算法得到三个粗定位结果坐标A( x1,y1),B( x2,y2),C( x3,y3)。

步骤4 给A( x1,y1),B( x2,y2),C( x3,y3)赋予相应的权值的到加权坐标

步骤5 对加权坐标进行三角定位运算，得到待定位点坐标(x,y)。

4 实验与结果分析

本文的实验环境为：一个布设了室内无线蓝牙定位环境的办公室，该办公室面积为50 m×50 m，在该场景内布设26 个蓝牙Beacon 节点，每个蓝牙Beacon 节点之间相距8 m。测试规则为：蓝牙Beacon 节点每隔3 s 上报RSSI 数据包，测试时测试人员在每个测试点测试30次。当90%的误差值低于某一个值时，则该值即为该点的定位误差值；计算区域误差值时，当整个区域内误差值有90%低于某一个值时，则该值为这个区域内的定位误差（即算法平均误差）。同时，选择文献[12]中的最小二乘定位算法和改进的四点质心定位算法进行比较，分别记为传统三角定位算法和四点定位算法。

本文采用方程式（11）来计算定位结果的精度。方程式（11）表示如下：

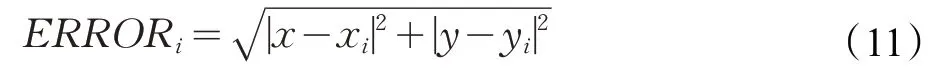
其中，(x,y)为实际待定位点的二维坐标，(xi,yi)为算法计算出的待定位点的估计二维坐标。

从表1 中可以看出：传统三角定位算法的定位误差在1.908 m 内，平均定位误差为0.970 m，运行时间为0.690 ms；四点定位算法的定位误差在1.709 m 内，平均定位误差为0.897 m，运行时间为0.640 ms；本文提出的定位算法也存在着定位误差，但是定位误差在1.602 m内，平均定位误差为0.880 m，运行时间为0.590 ms。与传统三角定位算法和四点定位算法相比，本文提出的算法具有更高的定位精度。

表1 不同定位算法的性能比较

同时，将本文提出的定位算法应用于实际的定位系统中，在定位系统的导航模块，进行导航过程的定位测试。测试规则为：选取起点与终点，规划多条路径，并在路径中设定测试点，在每条路径中测试多次，每个测试点的平均误差值作为该测试点的定位误差值，将整个区域内所有测试点的定位误差值的平均值作为该区域内定位系统导航模块的定位误差值。测试过程：在测试区域内部署多个蓝牙Beacon 节点，测试人员佩戴蓝牙手环，每2 s 上报一次RSSI 数据，服务器端收集到5 组RSSI 数据后才开始进行定位计算。测试结果如图6所示。

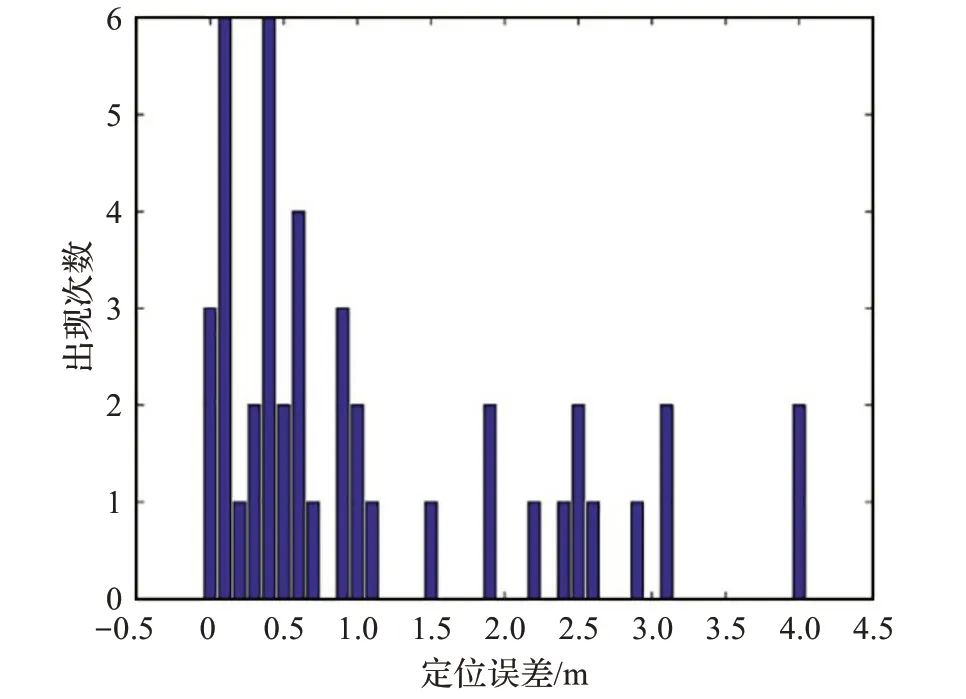
图6 导航模块测试结果图

从图6 中可以知道：本文定位算法在导航过程中的定位误差主要出现在[0，1]之间，在行走过程中因为测试点进入定位系统覆盖边缘时会出现较大的误差，但是整个过程定位误差将控制在4 m 内，平均定位误差为1.097 7 m。

5 结束语

为了降低传统的基于接收信号强度指示（Received Signal Strength Indication，RSSI）的三角定位算法产生的定位误差和和定位结果存在波动性的问题，本文提出一种基于三点定位与加权坐标的三角定位算法。该算法先对RSSI 数据进行卡尔曼滤波操作，降低RSSI 数据的波动性；然后将滤波后数据经过基于RSSI 选取的三点定位算法，获取粗定位坐标；最后将获取的三个粗定位坐标经过基于加权坐标的三角定位算法得到待定位点坐标。本文从理论原理和实验测试方面验证了算法的可行性，并通过实验结果分析可知该算法能有效地提高定位精度。