三维动态整数帐篷映射设计与分析

钟 鸣，刘建东，刘 博，2，陈 飞，2，张世博

1.北京石油化工学院 信息工程学院，北京102617

2.北京化工大学 信息科学与技术学院，北京100029

1 引言

在非线性科学领域中，混沌动力系统因其拥有对初始状态的极端敏感性、伪随机性、轨道不可预测性、拓扑混合性等多种特性而成为一个重要的研究方向。通过对混沌系统多次迭代计算，可以产生具有优良性能的伪随机序列，适用于通信安全、信息加密[1-3]。因此，在密码学领域，混沌系统有着极大的研究价值。

混沌密码体系在继承传统密码体系中的扩散与混乱的同时，又将定义区间由传统密码学的有限集扩展到实数域[4-6]。混沌系统数字化后带来的问题就是混沌特性严重下降，其动力学行为可能会被预知，这不利于构造安全有效的伪随机序列。针对这一问题，可以从施加扰动机制、提高计算精度、扩展空间维度三个方面来改善数字化混沌系统的动力学行为，从而降低特性退化对伪随机序列性能的影响。

比较经典的混沌动力系统是Logistic映射系统和帐篷映射系统。其中，Logistic 映射的混沌区域会存在与初值无关的固定空缺，且均匀分布特性较差。帐篷映射不存在如上问题，故帐篷映射的可靠性高于Logistic 映射。帐篷映射的映射空间较小，不能完全满足生成高安全性伪随机序列的要求。文献[7]中通过增加参数来改进帐篷映射，但改进后的帐篷映射生成的伪随机序列在不出现信息损耗的情况下能够被压缩，使得生成序列的随机性并不理想。文献[8]中提出整数帐篷映射并将其迭代生成的伪随机序列空间扩展至2(k+1)，这使得帐篷映射由实数域转化到整数域进行运算，但在其有限的映射空间内迭代计算会出现短周期行为。为了改善这一缺陷，文献[9]提出了增加动态扰动机制，文献[10]在扰动机制的基础上提出了扩展维数，构造二维整数帐篷映射，取得了一定成果，但这是基于耦合映象格子系统置乱进行的伪随机序列构造，所以生成序列特性的提升本质上是两个系统相互影响的结果。

为了进一步增强二维系统生成序列的复杂度，研究不同状态及参量变化对系统的影响，本文通过施加扰动机制、提高计算精度和扩展空间维度，构造了三维动态整数帐篷映射，并从信息熵、互信息、差值特性、分布特性、最大Lyapunov 指数及随机性方面进行仿真分析，探讨了扰动机制、计算精度和空间维度对映射系统动力学行为产生的影响。分析表明，在扰动、精度和维度的三重影响下，三维动态整数帐篷映射可以脱离外界模型的置乱干扰，独立产生性能良好的伪随机序列，适合应用于密码学领域作为密钥对数据文件进行加密。相较于一维和二维帐篷映射系统，三维动态整数帐篷映射系统的动力学行为更加复杂，安全性更高。

2 基于帐篷映射的映射系统

2.1 帐篷映射

帐篷映射系统的定义为：

此系统将映射空间分成两个部分，通过对数值的拉伸与折叠，使产生的序列维持在映射空间中。其中，α作为控制参数，负责引导映射空间的大小。当控制参数α ＞0.43 时，系统整体处于混沌状态；当控制参数α=1时，系统为满映射，并有较强的平衡性[11]。

2.2 扩展整数帐篷映射

针对帐篷映射系统取值空间不足的问题，构造扩展整数帐篷映射系统。首先将帐篷映射由实数域计算转至整数域计算，即：

再对基于整数域计算的帐篷映射进行扩展，得到扩展整数帐篷映射系统的定义。

当n为偶数时：

公式中，1=2k-1，参数k 即精度，限制了映射系统的映射空间。

当n为奇数时：

2.3 动态整数帐篷映射

帐篷映射由实数域转至整数域进行计算时会产生短周期现象，为避免这一现象，在整数帐篷映射中加入动态参量，得到动态整数帐篷映射：

其中

该映射系统中，ki为动态参量，控制映射的水平移动。通过动态参量变化生成控制参数，使得该映射系统处于不断变化之中，从而打破短周期现象。

控制参数表达式中，2n限制了映射系统空间容量，未知量n反映了映射系统的精度，例如28称之为8精度，210称之为10精度。

2.4 二维整数帐篷映射

通过扩展维数可以将一维帐篷映射扩展至二维帐篷映射，其定义为：

定义域为：

其中

在该二维系统中，mi和ki为动态参量，控制映射系统移动，其随迭代时间不同而随机生成，并通过控制参数gi和hi反映到系统中。

3 三维动态整数帐篷映射系统设计

在二维整数帐篷映射的基础上构造了三维动态整数帐篷映射，其定义为：

定义域为：

对于定义中的参量gi、hi和si的取值方式，给出如下矩阵计算形式：

其中，mi和ki定义方式同公式（5），新引入的动态参数vi也采用同样的定义方式。At表示随着迭代时间进行，矩阵A取值只取某一列向量，t=1,2,3。

矩阵A表示为：

其中，E 表示单位矩阵。

公式（5）基于精度n=8，采用了耦合映象格子系统作为二维整数帐篷映射的空间置乱函数，以达到序列之间相互独立的目的。本文提出的三维动态整数帐篷映射除了将精度提高到10 外，还排除了依靠外界系统进行空间置乱干扰的方式，采用了矩阵变换来对参量gi、hi和si的取值方式进行扰乱，即依靠系统自身就可以产生多条独立性很强的伪随机序列。

4 三维动态整数帐篷映射特性分析

4.1 初值敏感性

初值敏感性是混沌系统的一个典型特征，对初始值进行微小的影响都会使得整个系统运动发生质变。可以采用NPCR（像素变化率）衡量一个系统的初值敏感程度，NPCR越大，系统状态点之间的离散程度越大。

NPCR计算方式为：

采用公式（7），选取4 种不同的差值情况计算NPCR，结果如表1 所示。对比可知，三维系统生成的混沌序列的NPCR 值大于二维系统，即三维系统的初值敏感性大于二维系统。

表1 10精度下二维与三维系统NPCR对比

4.2 信息熵与互信息

信息熵最早由香农提出，用以描述信源的不确定度。将这一概念应用在伪随机序列测试中，用以表征映射系统所产生序列的混乱程度，即信息熵值越大，迭代序列越接近无序，动力学特性越复杂[12-13]。

公式（6）中存在着{x1,x2, …,xn}、{y1,y2, …,yn}以及{z1,z2,… ,zn}三条序列，各序列对应的信息熵分别为：

p(Xi)、p(Yi)和p(Zi)表示每个序列中第i 个数出现的频率。在信息论中，频率的计算方式可以表示为：

n为伪随机序列可取得的最大值，则信息熵最大值为lb n。本文所提出的三维动态整数帐篷映射基于10精度，因此n=1 024，信息熵最大值为10。

分别计算8 精度下二维和三维系统的信息熵、10 精度下二维和三维系统的信息熵以及排除动态参量mi、ki和vi的扰动效果后10 精度三维系统的信息熵，并进行对比分析。计算结果如表2至表4所示。

表2 8精度下二维与三维系统信息熵对比

表3 10精度下二维与三维系统信息熵对比

表4 10精度下无动态扰动三维系统信息熵

从表2 至表4 中可以看出，二维和三维系统的信息熵值均逼近于8 精度及10 精度下的理论最大值。但在不依赖耦合映象格子系统干扰的情况下，三维动态整数帐篷映射的信息熵高于二维整数帐篷映射的信息熵，说明在独立迭代生成伪随机序列的前提下，三维系统的无序程度高于二维系统。在无动态参量干扰的前提下，系统信息熵出现明显降低，系统混乱程度大幅减弱，即动态参量在提升系统复杂性上具有明显作用。

通过信息熵值可以求得互信息，进而度量映射系统生成序列之间共享信息量的大小。当两条伪随机序列完全独立时，互信息值达到最小值0。对于三维动态整数帐篷映射中的三条伪随机序列，互信息的计算方式为：

其中，H(X,Y)、H(X,Z)和H(Y,Z)分别为序列X、Y 和Z的联合信息熵。

在计算互信息时，采用文献[14]中提出的等间距分格子法，通过变化xi、yi和zi以及动态参量mi、ki和vi的初始值进行分析，结果如表5所示。无动态参量mi、ki和vi的扰动下，变化xi、yi和zi的初始值进行互信息分析，结果如表6所示。

文献[10]通过公式（5）及公式（12）计算得到二维整数帐篷映射的互信息值，各数值均分布在在0.12 附近。对比表5 可知，本文提出的三维动态整数帐篷映射在排除外界系统扰乱的情况下可以得到更小的互信息值。分析表6，无动态参量干扰下的三维系统互信息值均在1.0左右，即各序列之间相关性较强，安全性差。

表5 三维整数帐篷映射系统的互信息

表6 无动态扰动三维整数帐篷映射系统的互信息

综上可知，在动态参量mi、ki和vi扰动作用下，三维动态整数帐篷映射系统独立生成的三条序列之间的关联性极小，各序列之间的独立性优于二维整数帐篷映射生成的序列。

4.3 差值特性

差值可以用来表示伪随机序列中某两个状态点之间的关系。理想状态下，系统生成的随机序列状态点的差值分布特性图应呈线性递减状态，且图像越平滑，系统的混乱程度越高，各相邻状态点之间的关联度越弱，即降低了由前一个状态点推知后一个状态点的可能性。

k阶差值的定义为：

其中，k为差值阶数。

取k=1时，分别计算8 精度下二维和三维系统、10精度下二维和三维系统以及无动态参量干扰下的三维系统的1阶差值分布情况，结果如图1至图5所示。

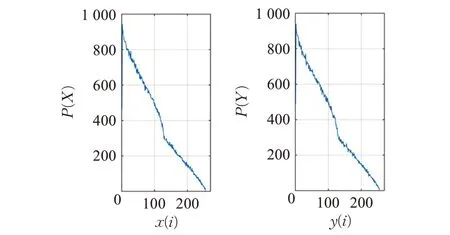
图1 8精度下二维系统X 和Y 序列1阶差值分布

图2 8精度下三维系统X、Y 和Z 序列1阶差值分布

对比二维和三维系统的差值分布，可以看出两种映射系统都服从差值分布线性递减的特性。但二维整数帐篷映射的差值分布图像在中间处有一个较明显的下折，而三维动态整数帐篷映射的差值分布图像更为平滑，这说明三维系统的差值分布较二维系统更严格服从线性递减的特性，其性能在一定程度上优于二维系统。

在无动态参量扰动的条件下，三维系统差值分布虽整体处于下降趋势，但图像不够平滑，起伏波动较大，各个状态点之间有较强的关联性。

4.4 相空间结构

相空间结构反映了伪随机序列中相邻状态点之间的数值相关性。数值相关性大的相邻状态点，其结构图会呈现出近似有序的分布，即伪随机序列中相邻点有很强的关联性；反之，数值相关性小的相邻状态点，其结构图呈现无序分布的状态，且随迭代进行，状态点会逐渐遍历整个分布空间。

通过三维动态整数帐篷映射系统迭代生成X、Y 和Z 序列，其相空间结构如图6 至图8 所示。三幅图均呈无序状态，且各状态点遍历整个分布空间，表明三条伪随机序列中各相邻状态点之间的数值相关性较弱，混乱程度较高。

在无动态参量干扰的情况下，绘制X、Y 和Z 序列的相空间结构如图9 至图11 所示。此时三维系统相图中出现明显可见的线性状态点分布，即没有动态扰动时，系统生成的序列中各相邻状态点之间有明显的关联性，容易由前一个状态点推知下一个状态点，系统安全性差。

图3 10精度下二维系统X 和Y 序列1阶差值分布

图4 10精度下三维系统X、Y 和Z 序列1阶差值分布

图5 10精度下无动态扰动三维系统X、Y和Z序列1阶差值分布

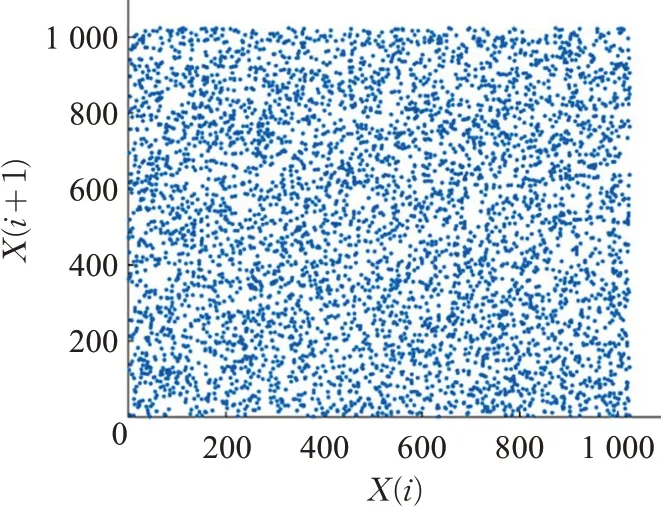
图6 三维系统X 序列相空间结构图

图7 三维系统Y 序列相空间结构图

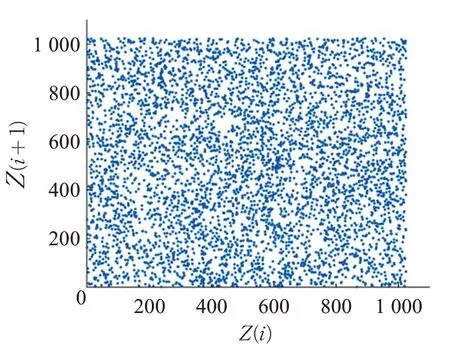
图8 三维系统Z 序列相空间结构图

图9 无动态扰动三维系统X 序列相空间结构图

图10 无动态扰动三维系统Y 序列相空间结构图

图11 无动态扰动三维系统Z序列相空间结构图

4.5 分布特性

序列的分布特性反映了序列中各数值出现的概率。理想的随机序列中每个值出现的概率相等，即其分布特性曲线应为一条直线。

分别计算10 精度下二维和三维系统以及无动态参量扰动的三维系统中各序列的分布特性，结果如图12至图14所示。

图12 10精度下二维系统X 和Y 序列分布特性

图13 10精度下三维系统X、Y 和Z 序列分布特性

理想状况下，10精度二维整数帐篷映射产生的序列中，每个数字出现的概率为1/1 024，约为0.976 56×10-3。分析图12 可以看出，分布曲线于1×10-3上下浮动，接近理想值。X 序列绝对误差约为1.094 37×10-4，相对误差约为0.112；Y 序列绝对误差约为0.994 37×10-4，相对误差约为0.101。

10精度三维动态整数帐篷映射产生的序列中，每个数字出现的概率同10 精度二维整数帐篷映射，约为0.976 56×10-3。分析图13可以看出，分布曲线于1×10-3上下浮动，接近理想值。X 序列绝对误差约为1.045 37×10-4，相对误差约为0.107；Y 序列绝对误差约为0.974 37×10-4，相对误差约为0.099；Z 序列绝对误差约为1.014 37×10-4，相对误差约为0.103。

图14 10精度下无动态扰动三维系统X、Y 和Z序列分布特性

综上可得，在动态参量扰动的条件下三维系统在分布性能上要优于二维系统，其产生的序列中各数字误差相对较小，出现概率更接近于平均。

4.6 Lyapunov指数

Lyapunov 指数可以用来描述一个系统的相空间中相邻轨道的变化情况，从而评估其混沌动力学行为的优劣。当把混沌系统提升到更高维度后，其最大Lyapunov指数越大，系统的混沌性能越优秀[15-16]。

文献[17]中提出了一种计算最大Lyapunov 指数的方法，这种方法适用于定义在整数域上的混沌系统，其计算表达式为：

其中，λ表示系统的最大Lyapunov 指数，S 表示系统维数，M 表示系统运行后得到的数据长度，d()表示相邻数据点的欧氏距离，F 表示系统的映射关系，mi表示系统的数据点。

针对本文设计的三维动态整数帐篷映射，计算其最大Lyapunov 指数与动态参数的关系分布图，得到的结果如图15至图17所示。

图15 三维系统X 序列最大Lyapunov指数

图16 三维系统Y 序列最大Lyapunov指数

图17 三维系统Z 序列最大Lyapunov指数

分析图15 至图17 可知，三维动态整数帐篷映射系统迭代生成的三条序列的最大Lyapunov 指数均在2 上下浮动，即三维动态整数帐篷映射为混沌系统。

4.7 NIST随机数测试

美国国家标准与技术研究所（NIST）公布的随机数测试工具可以对混沌系统迭代产生的序列进行测试，从而判断混沌系统动力学行为的复杂程度[18]。当15 项测试产生的P-value值大于1%时，可以认定测试序列随机性良好，产生序列的映射系统的动力学行为优秀。

文献[10]提出的二维整数帐篷映射通过施加耦合映象格子系统进行空间置乱，从而通过了NIST 随机数测试。当排除耦合映像格子系统的干扰时，对二维系统本身运行产生的结果进行NIST 随机数测试，得到的15项测试数据如表7所示。

表7 8精度二维映射系统NIST随机数测试结果

由表7 可知，二维整数帐篷映射的X 序列和Y 序列均未通过Longest Run of Ones 测试和Non-Overlapping Template Matchings 测试，即二维系统本身存在着较大的缺陷。

将二维系统空间维数提升，构建精度为8 的三维动态整数帐篷映射，进行NIST 随机数测试，结果如表8所示。

由表8 可知，二维整数帐篷映射系统在仅提高空间维度的条件下可以通过NIST 随机数测试，但部分测试结果接近临界值，因此本文考虑在提高空间维度的基础上将计算精度从8 提高到10，得到三维动态整数帐篷映射，并对其运行结果进行NIST随机数测试，测试结果如表9所示。

由表9 可知，计算精度由8 提高到10 后得到的三维动态整数帐篷映射系统通过NIST 测试，且各序列属性优秀。

4.8 功率谱

动力系统生成时间序列的过程可以视为重复叠加的周期运动，通过分析其功率谱可以辨别系统是否为混沌状态[19-20]。当系统为周期系统或拟周期系统时，功率谱表现为线性状态，或存在明显的波峰；当系统为混沌系统时，功率谱表现为连续不规则状态，且图像更加稠密，没有明显波峰存在。

本文采用了基于FFT 计算功率谱的方法，先计算出傅里叶系数：

根据傅里叶系数计算功率谱[21]：

对三维动态整数帐篷映射系统迭代1 000 次，得到三条序列的功率谱如图18 至图20 所示，三条序列的图像均为不规则的稠密折线图，由此可知三维系统有较强的混沌性。

表8 8精度三维映射系统NIST随机数测试结果

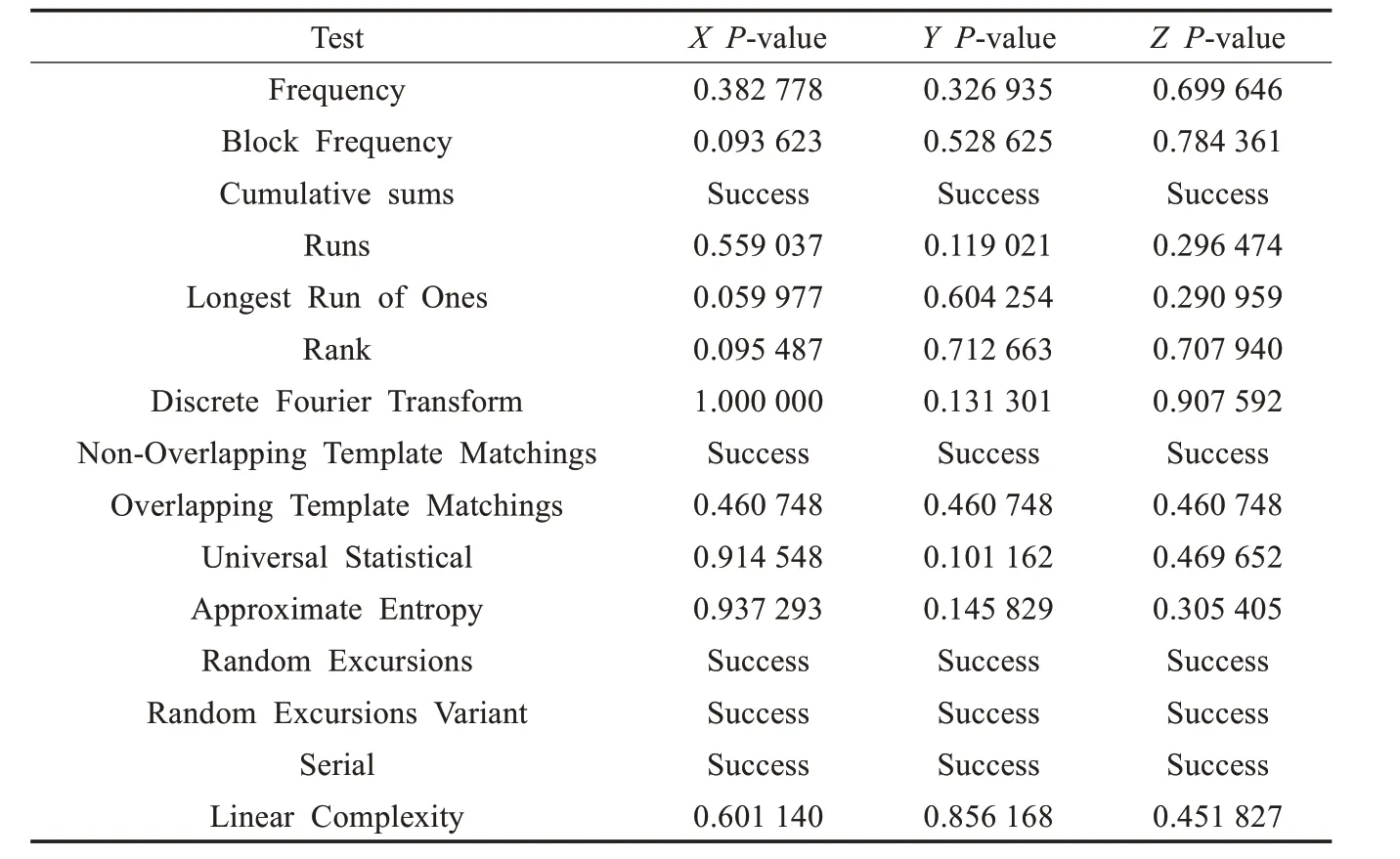
表9 10精度三维映射系统NIST随机数测试结果

图18 三维系统X 序列功率谱

图19 三维系统Y 序列功率谱

图20 三维系统Z 序列功率谱

在无动态参量mi、ki和vi扰动的条件下对三维系统迭代1 000次计算其序列功率谱，结果如图21至图23所示。可见在无动态干扰时，序列混沌特性大幅减弱。

5 结束语

本文基于二维整数帐篷映射，在施加动态扰动、提高计算精度及扩展空间维度的基础上构造了三维动态整数帐篷映射，并采用矩阵变换的形式对产生的序列进行置乱。对三维动态整数帐篷映射系统的信息熵、互信息、差值特性、分布特性、最大Lyapunov 指数及随机性进行仿真分析，结果表明，新的三维系统生成的序列有极强的复杂性、独立性，其动力学特性相当优越。

该系统基于图像加密提出，其生成的伪随机序列作为密钥，拥有良好的安全性。但新系统不局限于此，也可用作伪随机序列发生器或进行视频加密及图像隐藏[22]。在将来研究工作的中，考虑在大数据平台上利用该系统实现图像加密以及图像分存，以提高该系统的实现效率以及其性能的优越性。

图21 无动态扰动三维系统X序列功率谱

图22 无动态扰动三维系统Y序列功率谱

图23 无动态扰动三维系统Z序列功率谱