聚苯乙烯泡沫板铺设高度对涵洞的减荷影响

罗吕青，张谢东，李彬，晓夏，刘建平，黄笑犬

(1. 武汉理工大学 交通学院，湖北 武汉 430063；2. 中交第一公路工程局集团有限公司，北京 100024)

马斯顿效应[1]是一种由填埋土体的不均匀沉降导致对下方填埋结构产生的附加应力现象，常常出现于设有刚性涵洞的高填方路段，其形成原理如图1所示。早期马斯顿效应未被纳入涵洞设计考虑，设计者过小预计了涵洞所受荷载，导致许多投入使用的高填方涵洞出现了开裂等不同程度的破坏，极大地影响了涵洞的安全性[2-3]。

在填埋结构物顶部铺设柔性材料可以有效地减小马斯顿效应[4]，其中，采用聚苯乙烯泡沫(Expanded Polystyrene，简称为EPS)板充当柔性填充材料的方案具有可设计性与稳定性的特点，被认为是较为便捷可靠的减荷方案[5]。EPS材料的减荷能力与其材料性质密不可分，其特殊弹-塑性性质和较为明显的蠕变与松弛性质都是其减荷能力较为优越的原因[6]。此外，EPS材料力学性质和化学性质非常稳定[7]，可为涵洞提供长期减荷环境，且其易于制造、运输和施工的特点也为其广泛应用提供了便利。

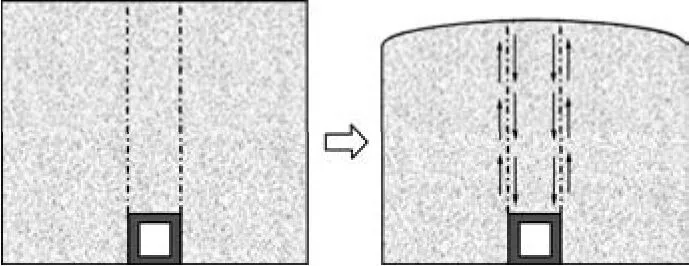
图1 马斯顿效应的形成示意Fig. 1 Formation of Marston effect

EPS材料在20世纪60年代初次应用于土木工程。Sladen[8]等人在对马斯顿效应的研究中，首次使用EPS泡沫颗粒作为涵洞顶部的减荷填料，取得了较好的减荷效果。此后经过顾安全[5]对减荷措施的实验研究，验证了用EPS板作为洞顶柔性填料对高填方下涵洞的减荷效果的优异性。EPS板减荷如图2所示。

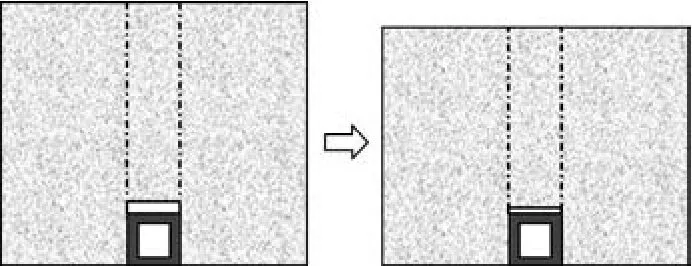
图2 铺设EPS板减荷示意Fig. 2 Diagram of laying EPS board to reduce load

EPS板的材料性质与其密度有很强的相关性。密度越大，其强度越大[9]。但EPS板在被用于减荷时并非密度越大，厚度越大，减荷效果越好。王庆石[10]结合室内模型实验与有限元分析，得出的结论为：填土高度较低时，低密度EPS板对于涵洞的卸载效果更好。当填土较高时，较高密度、较大厚度的EPS板卸载效果更好。潘放[11]等人也通过有限元模拟计算，发现：EPS板厚度虽与洞顶土压力呈负相关，但在厚度达到一定值后，再增加厚度时，其减荷效果不变。王俊伟[9]通过研究管涵周围土压力的分布情况，提出：将EPS板设计成顶部相对较厚、两侧相对的较薄的结构，更能发挥材料的减荷效果，并使涵洞的受力更加合理。同时，他提出：将多种密度的 EPS材料叠加成组合材料的方案更能发挥出各密度材料的潜力，可以避免EPS板的塑性因压缩而过快地被消耗完，提高了材料的利用率。针对EPS本身材料性质的应用研究较多，但对EPS板铺设方式的研究较少。因此，作者根据EPS板对高填方涵洞的减荷原理，结合前期在EPS板减荷方面的研究，依托喀麦隆雅杜高速某断面，拟建立EPS板在不同铺设高度下的高填方涵洞模型，分析EPS板铺设高度对其减荷效果的影响。

1 EPS板减荷原理

EPS板减荷原理与马斯顿效应产生原理相同，均可归结为土拱效应的产生。土拱效应是由土体间的不均匀位移导致的应力转移现象[12]，通过剪切强度传递能量而引起的土体间的应力重分配[13]。土体颗粒之间存在的粘结力与摩擦力会抵抗土体在自重或者荷载的作用下产生不均匀变形而形成土拱效应。

EPS板的蠕变与松弛效应较为明显[9]。当施加的荷载足够引发其塑性变形时，其变形与时间有较明显的联系。实际施工中由于填土较高，对EPS板的压力较大，EPS板的蠕变与松弛性质较为明显。在加载完成后，EPS板变形仍会增大，其对板上填土的支持力会逐渐减小。由于土体颗粒之间存在的粘结力与摩擦力会将土体拉紧，抵抗土体下落，因此，涵洞顶部填土的重力由两侧填土的摩擦力与涵洞顶部的支持力共同平衡，形成了一个在涵洞顶板上的减载土拱。减荷原理如图3所示。

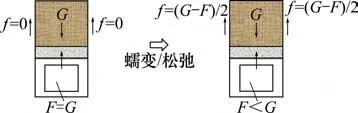
图3 减荷原理示意Fig. 3 Diagram of load reduction principle

2 有限元仿真分析

喀麦隆雅杜(雅温得—杜阿拉)高速公路全长约195 km，地形和地质条件比较复杂，存在着多处高填方涵洞。其中，某涵洞截面如图4所示。

该涵洞净跨径为2 m，高为1.5 m，顶板厚度为40 cm，侧墙厚度为 30 cm，路基中央填土高度为11.61 m，涵洞结构尺寸如图5所示。实际工程中，在此截面的涵洞顶部铺设了厚20 cm、密度24 kg/m3的EPS板，且取得了较好的减荷效果。

图4 雅杜高速某涵洞截面(单位: cm)Fig. 4 One section of Ya-Du Expressway (unit: cm)

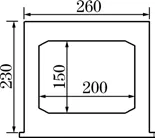
图5 涵洞尺寸示意(单位：cm)Fig. 5 Diagram of culvert (unit: cm)

采用有限元软件ABAQUS，依据雅杜高速某涵洞截面的实际尺寸，以该断面道路中线截面为研究对象，建立填土-EPS板-涵洞数值模型。假设涵洞与填土坐落于已沉降完成的刚性地基上，ABAQUS模型中的地基用限制其底面竖向位移的边界条件模拟；填土材料符合摩尔库伦屈服准则，采用Mohr-Coulomb模型进行模拟；涵洞仅考虑线弹性变化，采用线弹性模型进行模拟；EPS板考虑弹、塑性变形，采用Crashable-Foam模型进行模拟。

为简便计算，忽略涵洞洞脚延伸段，从地基算起，填土总高度取14 m，其数值模型如图6所示。在图6中，空心矩形区域为涵洞，计算时赋予其混凝土材料参数。涵洞顶部按与涵洞等宽每隔10 cm高度划分一片区域，共分为5片区域(1#, 2#, 3#, 4#和5#)，按照所需工况赋予其填土或EPS板材料参数，以达到方便、快速计算多种工况下该模型的各项结果。模型其余区域均赋予填土材料参数按照分层区不同的材料赋予情况，分为5种工况(见表1)。ABAQUS软件中，Crashable-Foam模型的材料需要提供真实应力和塑性应变的关系。其与名义应力σ、名义应变ε的换算公式为：

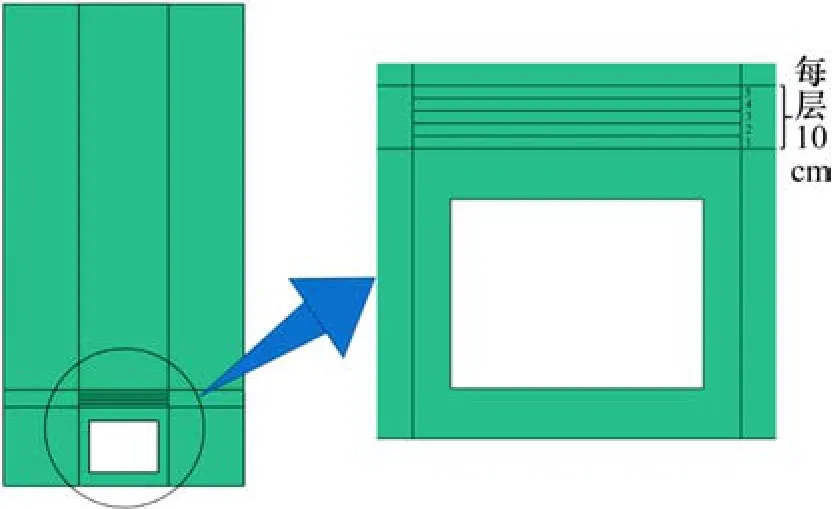
图6 数值模型Fig. 6 Details of numerical model

表1 不同参数赋予方案Table 1 Different parameters of the assignment scheme

1) 真实应力

2) 塑性应变

24 kg/m3的EPS板应力-塑性应变关系见表2。模型中其余材料尺寸及力学参数见表3。

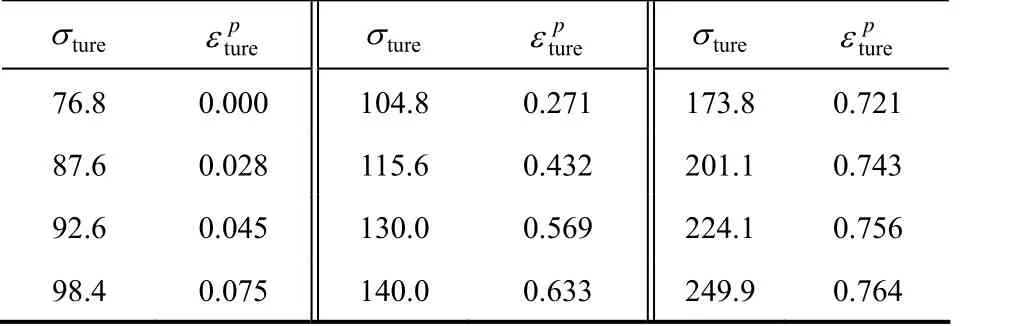
表2 24 kg/m3的EPS塑性应变Table 2 Real plastic volume strain of EPS at 24 kg/m3

限制模型底部竖向位移与两侧水平位移，模型顶部不作边界限制，仅考虑重力作用下模型受力及响应，不考虑排水渗流。因马斯顿效应在涵洞周边最为明显，对涵洞及其顶部与侧向区域进行密集化网格划分，对其余部分进行粗略化网格划分，划分完成后模型网格如图7所示。

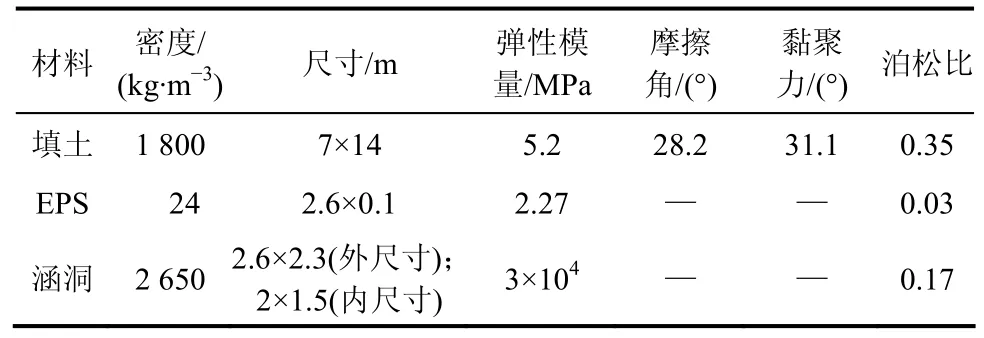
表3 材料计算参数Table 3 Material calculation parameters

图7 数值模型网格划分Fig. 7 Grid generation of the numerical model

3 计算结果与分析

3.1 EPS板铺设高度对填土垂直压应力的影响

不同工况下填土垂直压应力如图8所示。

在图8(a)中，未铺设EPS板时，涵洞周边土体垂直压应力的最大值为0.366 9 MPa，出现在涵洞顶板上方两角处。涵洞顶板中心处(图中左侧箭头所指处)的垂直压应力为0.245 1 MPa，约为涵洞顶部垂直土柱压力(σ=γh=0.21 MPa)的 1.16 倍，距涵洞侧壁1 m 的地基处(图中右侧箭头所指处)垂直压应力为0.188 7 MPa，远小于其所处位置的上部土柱压力(0.25 MPa)。该现象是由于刚性涵洞的存在，使得涵洞顶部与其两侧土体沉降量不同，土体之间通过剪切应力引起土体内的应力转移，产生了土拱效应，导致涵洞承受更大范围的土柱压力。相应地，地基处的土体垂直压应力也由于应力转移有较大幅度的减小。

在图8(b)中，铺设EPS板后土体地垂直压应力分布有较大的变化，表现为原分布在涵洞顶部的大应力区域转移到了EPS板左、右两侧土体中，压应力的最大值为0.429 3 MPa。虽然垂直压应力的最大值较未铺设EPS板时的有一定增大，但其所处的位置不再位于涵洞正上方，而转移至涵洞两侧土体中，涵洞本身所受垂直压应力大幅减小，原应力最大点处的应力减小为0.102 MPa。

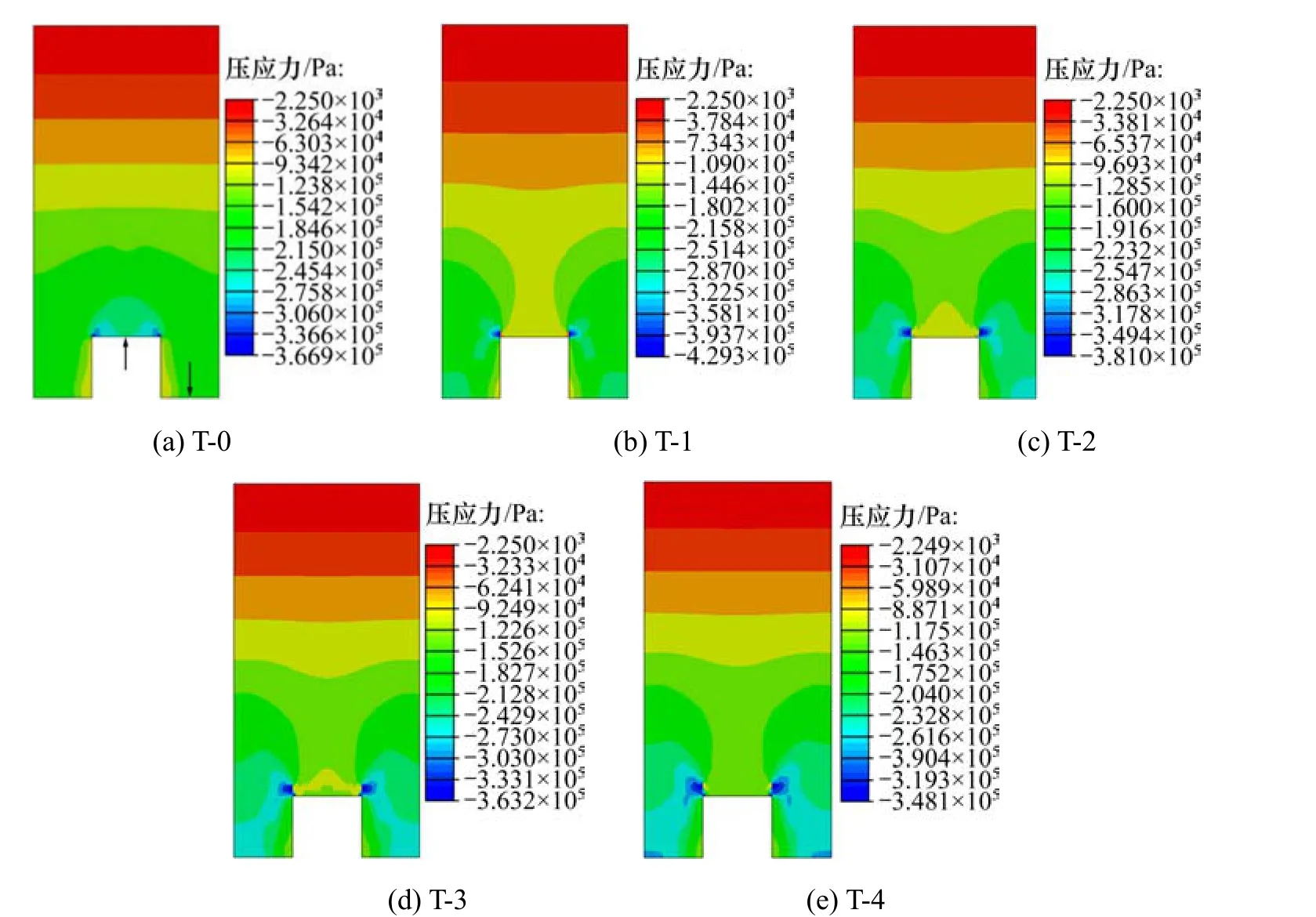
图8 不同工况下填土垂直压应力云图Fig. 8 Cloud chart of vertical compressive stress

涵洞顶部的垂直压应力有较明显的削减，其顶板中心处垂直压应力为0.122 7 MPa，约为未进行减荷时的50%。距涵洞侧壁1 m地基处所受的土体垂直压应力为0.254 8 MPa，接近其上部土柱压力。引起该应力转移现象的原因是：加铺的EPS板在土压力的作用下产生了较大的压缩，消除了涵洞顶部与两侧土体原本存在的沉降差，截断了马斯顿效应的产生条件。

在图8(b)～(e)中，随着EPS板铺设高度的增加，土体中垂直压应力的最大值逐步减小，涵洞顶部小应力范围也逐步缩小。当高度上升到一定值后，涵洞顶板两角重新出现了大应力区域。涵洞顶板垂直土压力的变化如图9所示。在4种不同的铺设高度模拟下，除贴合洞顶铺设的工况外，涵洞两角处的垂直压应力仍存在较大的数值，但其在顶板净跨范围内的垂直压应力始终保持着较小的数值，虽其数值随着铺设高度的增加而增大，但变化幅度较小，且相较未减荷时的数值变化不大，仍有较好的减荷效果。

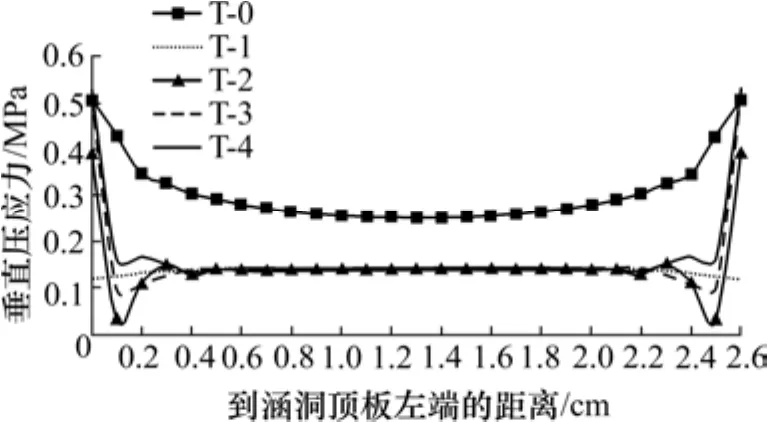
图9 涵洞顶板垂直土压力的变化Fig. 9 Vertical earth pressure change of culvert top plate

3.2 EPS板铺设高度对涵洞MISES应力的影响

不同工况下涵洞半结构 MISES应力如图 10所示。

在图10(a)中，未铺设EPS板时，涵洞MISES(第四强度相当应力)应力的最大值为3.415 MPa，出现在涵洞内壁两上角，区域较小，属明显的应力集中，对涵洞结构安全较为不利。涵洞顶板 MISES应力呈半圆环状分布，其中：顶板上沿最大，顶板下沿次之，顶板中心最小。

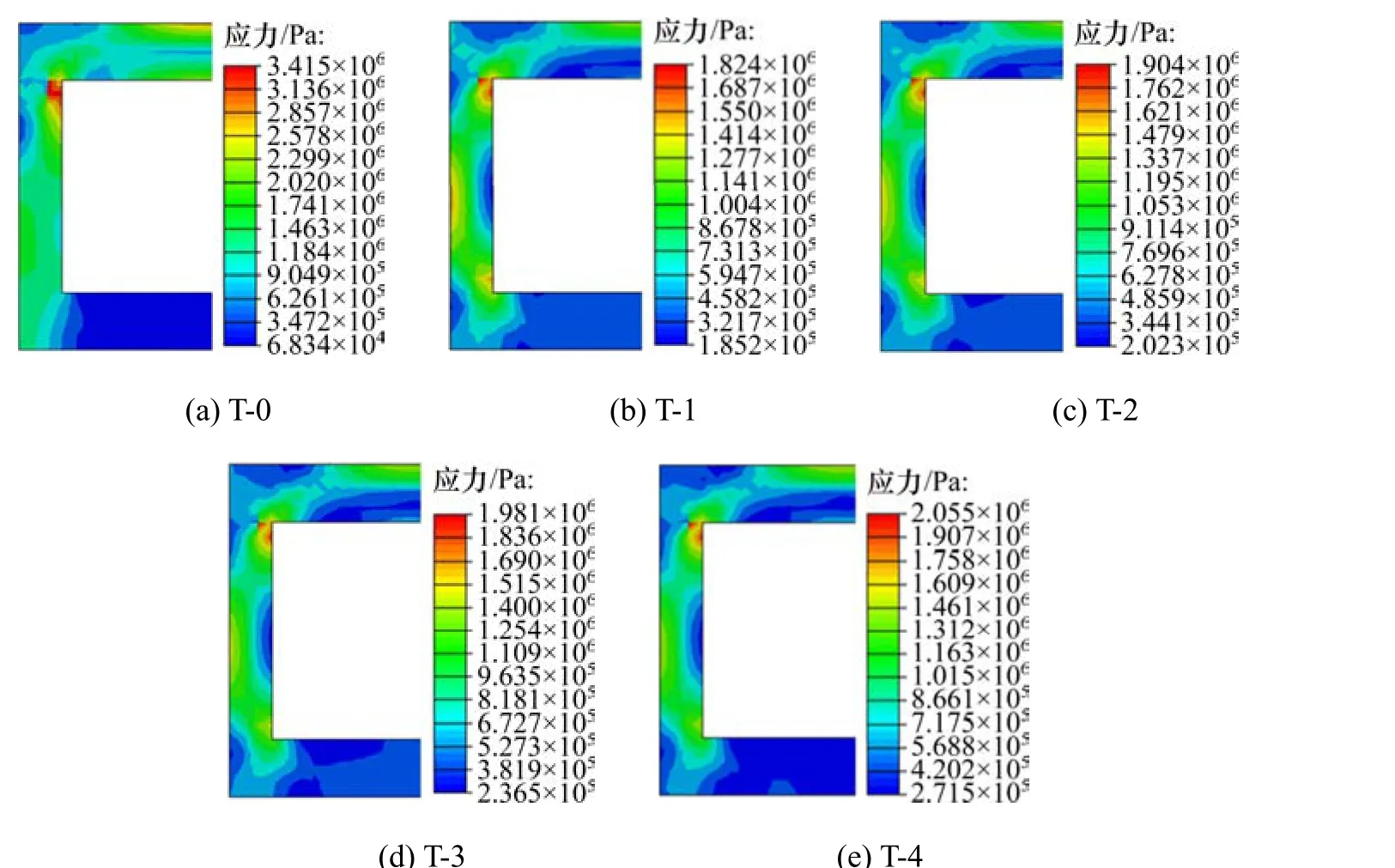
图10 不同工况下涵洞半结构MISES应力Fig. 10 Cloud chart of half culvert MISES stress

在图10(b)中，铺设EPS板对涵洞进行减荷后，涵洞MISES应力的最大值变为1.824 MPa，约为未减荷时的53.4%。大应力区域也发生了较明显的转移，原本集中在涵洞内径上角的大应力区域重分布到了涵洞内径四角与侧壁，且数值有较大的降低。铺设EPS板后涵洞顶板MISES应力的最大值仍产生在顶板上沿，但 MISES应力的最小值出现在了顶板下沿中心，且涵洞四壁内部边缘的 MISES应力都处于较小的值。

在图10(b)～(e)中，随着EPS板铺设高度的增加，涵洞 MISES应力的最大值逐渐增加，且可见明显的演化趋势。即：随着铺设高度的增加，原本分布较为均匀的 MISES应力逐步向涵洞内径两上角集中，涵洞顶板下沿逐渐出现较大的应力区域。

3.3 EPS板铺设高度对涵洞顶板竖向剪应力的影响

不同工况下涵洞竖向剪应力云图如图11所示。

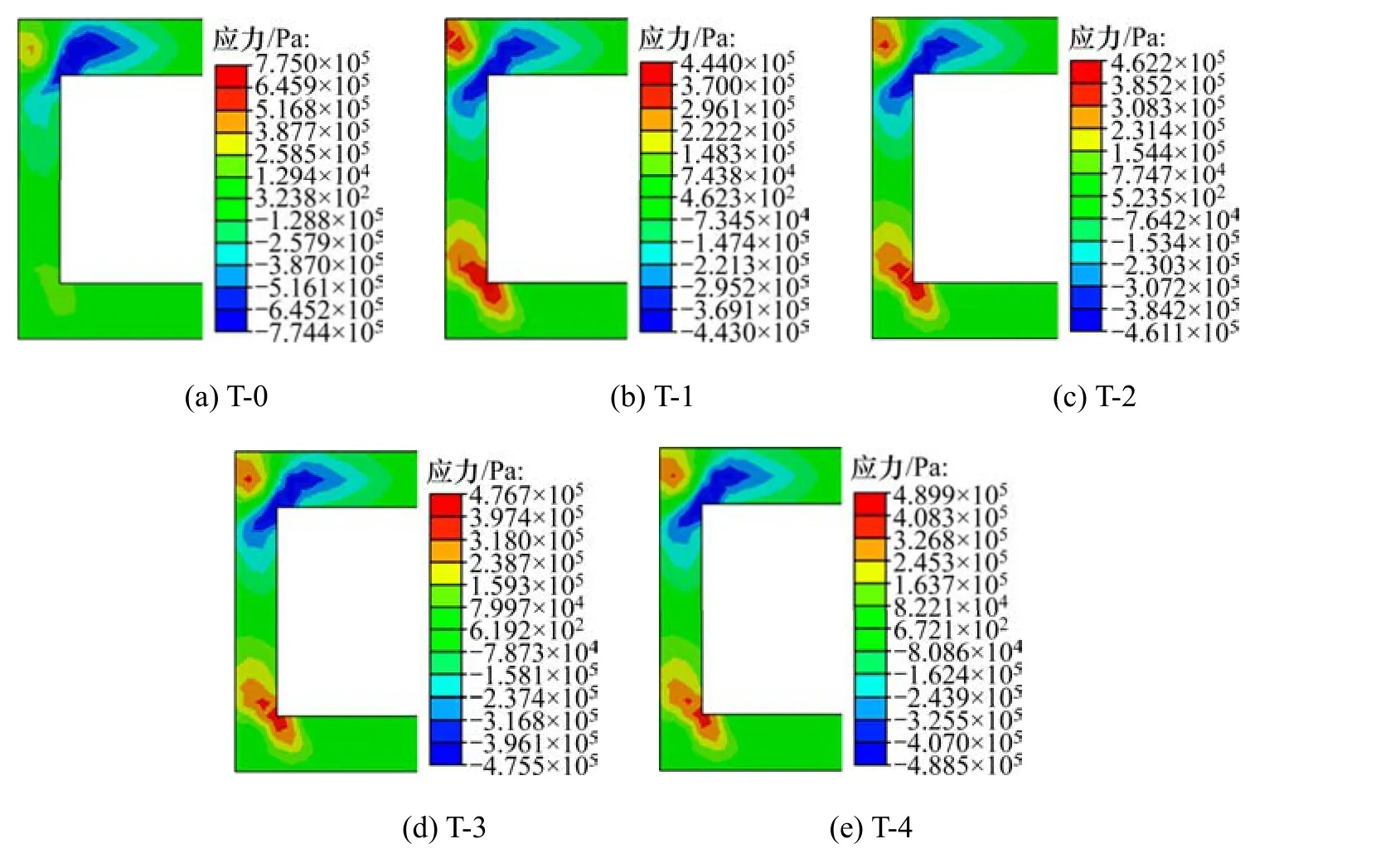
图11 不同工况下涵洞竖向剪应力云图Fig. 11 Cloud chart of half culvert vertical shear stress

在图 11(a)中，未铺设 EPS板时，涵洞顶板竖向剪应力的最大值出现在净跨两端，竖向剪应力的最大值为0.775 MPa，大应力区域呈叶片状，涵洞截面中心两侧呈对称分布。

在图11(b)中，铺设EPS板后涵洞顶板竖向剪应力有较大的数值与分布变化，竖向剪应力的最大值为0.444 MPa，出现在涵洞外部上角，相比未铺设时的有较大的减小。

在图11(b)～(e)中，随着EPS板铺设位置的增高，涵洞顶板剪应力逐步增大，但总体变化缓慢，增长比例微小，仍远小于未铺设 EPS版时的竖向剪应力，与图9中所示垂直土压力的变化规律一致。

3.4 EPS板铺设高度对涵洞顶板挠度的影响

涵洞顶板净跨挠度如图 12所示。未铺设EPS板时，涵洞顶板跨中挠度可达0.442 mm，挠度最小处有0.155 mm。铺设EPS板时，涵洞顶板挠度有较大幅度的减小，挠度最小的工况是 T-1，即 EPS板紧贴涵洞顶板铺设，其跨中挠度为0.195 mm，顶板端点挠度为0.085 mm。由线弹性公式分析端部位移可知，未铺设EPS板时，涵洞侧壁所受竖向土压力接近减荷后的两倍，与图9中所示结果吻合。

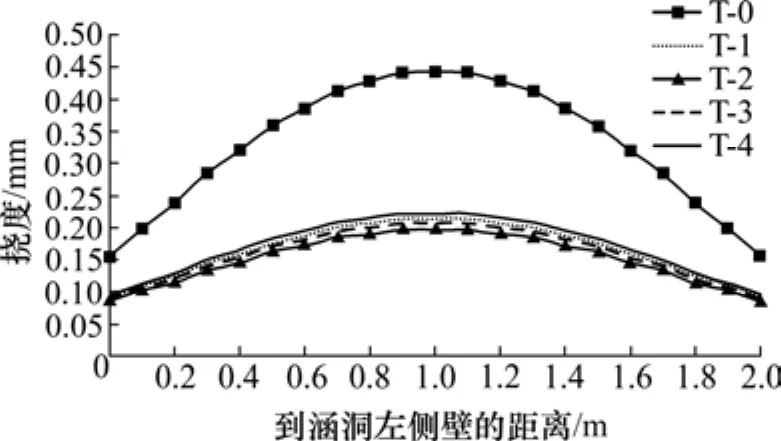
图12 涵洞顶板净跨挠度Fig. 12 Clear span deflection of the culvert roof

将涵洞顶板相对于顶板端点的挠度称为涵洞顶板的相对挠度。根据力的叠加原理，此数据可更直观地反映涵洞顶板的变形状态。涵洞顶板净跨相对挠度如图13所示。未铺设EPS板时，涵洞顶板跨中的相对挠度为0.287 mm，T-1工况下该点的相对挠度为0.109 mm，约为未铺设EPS板时的38%，表明铺设EPS板对顶板弯曲的改善效果非常明显。

随着EPS板铺设高度的增加，涵洞顶板的相对挠度逐步增加，涵洞变形增大，但仍远小于未铺设时的挠度。

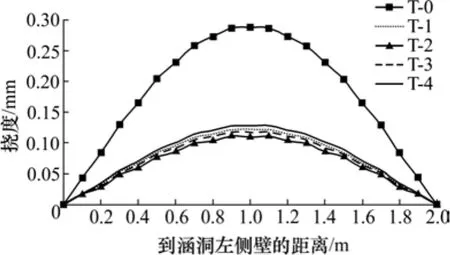
图13 涵洞顶板净跨相对挠度Fig. 13 Relative clear span deflection of the culvert roof

4 结论

借助有限元软件ABAQUS，建立了填土总高度为14 m的高填方涵洞模型，分析了EPS板在不同铺设高度下对填土的竖向压应力、涵洞的 MISES应力、涵洞顶板的竖向剪应力和涵洞顶板的挠度的影响。得到的结论为：

1) EPS板可通过大变形产生应力重分布，大幅降低马斯顿效应带来的附加应力，对涵洞的应力环境有良好的改善。

2) 改变 EPS板的铺设高度对涵洞顶板竖向剪应力与涵洞净跨顶部垂直土压力的变化影响不大，但对土体中垂直土压力分布有较大的影响。

3) 改变EPS板的铺设高度对涵洞MISES应力有一定的影响。铺设高度越高，MISES应力的最大值越大，但始终处于较低的范围。

4) 改变 EPS板的铺设高度对涵洞顶板挠度的影响较为明显。铺设高度越高，涵洞顶板挠度越大，但整体数值仍远小于未铺设 EPS板时的涵洞顶板挠度。

即使 EPS板贴合涵洞顶部铺设时减荷效果最优，但其铺设高度对涵洞的应力环境影响不明显，建议施工铺设时可按施工环境自行选择较为方便的铺设高度。