基于节线法的地锚式悬索桥缆形计算分析
董福民,宁晓骏,熊云睿,周兴林
(昆明理工大学 建筑工程学院,云南 昆明 650500)
悬索桥是利用主缆和吊索作为加劲梁并将荷载传递至桥塔和锚定的悬挂体系。对于地锚式悬索桥,锚定有隧道锚和重力锚之分,其主缆端部均锚固在大地上,主缆拉力由锚定传递给地基。因此,在两边桥台处,修筑大型钢筋混凝土锚体结构。加劲梁悬索桥在竖向荷载和水平荷载的共同作用下的结构体系属于超静定结构。主缆是悬索桥的主要承重结构,且属于大变形柔性构件。在结构分析中,对主缆计算的精细化直接关系到悬索桥的计算精度。确定成桥阶段主缆线形和无应力索长是计算分析和设计的关键,对后期的施工控制意义重大[1-4]。作者拟针对悬索桥受力的几何非线性特点,分别采用抛物线法、分段悬链线法及节线法,对地锚式悬索桥的主缆线形和主缆坐标进行计算,分析节线法在设计和施工过程中的优势。
成桥状态的计算是根据悬索桥布置形成的纵断面线形来确定主缆的几何线形的。依次分析构件在成桥状态的受力情况、结构形状,求解主缆坐标和无应力索长度。在成桥状态的近似计算中,假定[5]:①主缆为理想柔性索,只承受拉力,不计其弯曲刚度,不承受扭矩和压力;②缆索材料符合胡克定律;③索横截面在荷载作用下不发生变化。
以中跨为例,计算和分析悬索桥的成桥状态。
悬索桥的主缆力学简化模型如图1所示。取微小单元 dx,由主缆平衡条件得单边悬索的基本方程:

式中:H为主缆水平力分量;q为均布荷载集度。
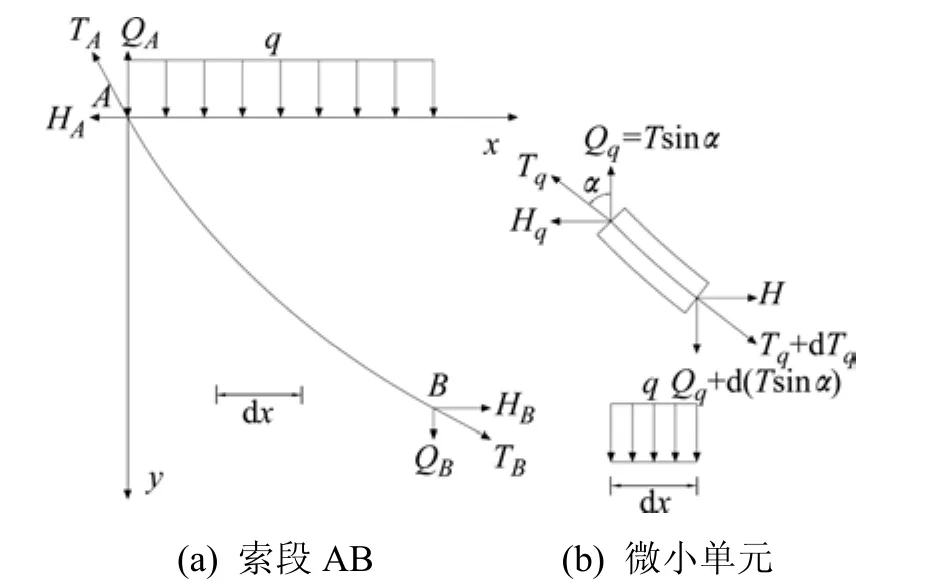
图1 主缆力学简化模型Fig. 1 Simplified model of main cable mechanics
若荷载沿水平方向均匀分布或荷载沿主缆长度均匀分布,则式(1)有抛物线和悬链线2种线形解。
鉴于悬索桥缆形计算的复杂性,采用有限元法进行分析。节线法是一种基于有限元法分析悬索桥的数值迭代法。在满足跨中垂度和跨径条件下,悬索桥加劲梁在自重作用下会产生变形,达到初始平衡状态,求出主缆的张力和坐标,称其为初始平衡状态分析。悬索桥加劲梁在加载二期荷载后会产生再次变形,达到平衡状态。以初始平衡状态为基础,进行多次迭代,计算出成桥线形,叫做悬索桥精确平衡状态分析。这2个阶段均以节线法为理论基础进行分析[6-10]。
1 计算方法
1.1 抛物线法
抛物线法即假定桥面荷载 qa和主缆自重 qb沿
1.1.1 主缆线形解
成桥主缆线形解为:
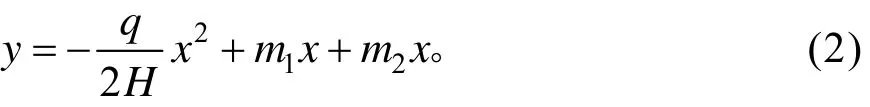
中跨主缆为:

边跨主缆为:

式中:l为中跨跨径;l1为边跨跨径;f为中跨矢高;f1为边跨矢高;h为主缆上任一点至主塔的垂直高度;m1和m2为常数。

图2 抛物线法主缆受力Fig. 2 Main cable force diagram of the parabolic method
1.1.2 无应力索长计算
在图1中,取一微段dx,该过程的推导参见文献[8]。
成桥状态悬索长度为:

式中:L为边跨或中跨跨径;C为主缆端部到塔顶的距离。
主缆伸长量为:

式中:E为主缆弹性模量;A为主缆横截面积。
无应力索长为:

1.2 分段悬链线法
分段悬链线法主缆受力如图3所示。均布荷载q沿主缆分布,可以等效转化为沿跨度方向均匀分布的荷载qy。那么,可得平衡微分方程为:
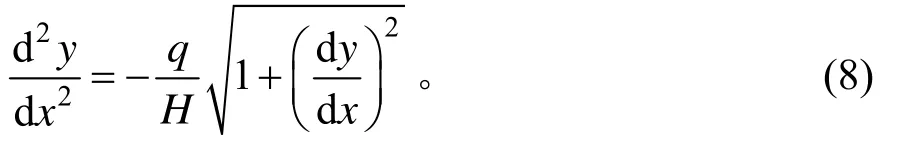
通过求解式(8)的通解,得:

式中:c1,c2均为常数。
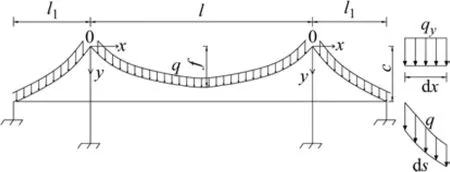
图3 分段悬链线法主缆受力Fig. 3 Main cable force diagram of the segmental catenary method
在图2中,中跨主缆边界条件为: 0x= , 0y= ;x l=, 0y= 。
将边界条件代入式(9),则跨中主缆线形解析式为:式中:l为中跨跨径。

同理可得,边跨的边界条件为: x = 0 , y = 0 ;为边跨主缆最低点至塔顶的垂直距离)。
将边界条件代入式(10),则边跨主缆线形解析式为:

分段悬链线法主缆线形的特解和无应力索长度的求解过程与抛物线方法一致,对分段悬链线法解析式和无应力索长度的求解参见文献[9]。
1.3 有限元节线法
采用有限元软件 Midas/Civil 2019,运用节线法,对悬索桥进行了主缆线形的分析求解。该方法采用日本Ohtsuki的计算平衡状态方程式,利用桥梁自重和主缆的张力,建立平衡方程来计算主缆的坐标和主缆的张力,分析悬索桥缆形[11-12]。该方法假定:①吊杆在横桥向倾斜,并垂直于顺桥向;②主缆张力沿着顺桥向是相同的;③主缆与吊杆的连接点间索形状呈直线,并非抛物线;④主缆两端坐标、跨中垂度、吊杆在加劲梁上的吊点位置及加劲梁的恒荷载已知。
主缆的张力分布如图4所示。

图4 主缆张力示意Fig. 4 Schematic diagram of main cable tension
1.3.1 竖平面内的平衡分析
将图4中的主缆张力分布图投影在x-z平面上,分析力的平衡。
假设由N-1根吊杆将主缆分成N段,取其中一点进行受力分析,如图5所示。

图5 x-z平面内主缆的受力平衡Fig. 5 Stress balance of main cable in plane x-z
在图 5中,Wsi为吊杆和加劲梁荷载平均到主缆的均布荷载,Wci为主缆的均布自重,在基本假定的前提下,根据力的平衡条件,其平衡方程为:

式中:Ti为节点 i-1与节点 i之间的单元张力;xi为主缆节点i在x方向的距离;di为xi-1到xi的水平距离;Tx为主缆张力水平分量;i=1,2,…,N-1。
计算中假定 Tx在主缆的每一个单元都是恒定不变的。
在x-z平面的平衡关系如图6所示,其平衡方程为:

图6 x-y平面内主缆的受力平衡Fig. 6 Stress balance of main cable in plane x-z

式中:pi为第i点吊杆张力;hi为吊杆长度。
联立式(12)和(13),可得:

在式(14)中,未知数为zi和Tx,共有N个未知数,N-1个方程,故还需一个条件才能求解方程组。由跨中垂度与跨中、两端吊杆的Z坐标关系得:

1.3.2 水平面上的平衡分析
水平面上的平衡分析与竖直平面的计算方法一样,也可得到N-1个平衡方程:

在式(16)中,y0和 yn为已知的量,yi由平衡方程可求出。
用节线法分析了悬索桥初始平衡状态,通过该方法求解出的初始主缆的坐标和张力只是初始平衡的近似计算,第一次计算出的初始线形与主缆的最终线形误差较大,因此,还需要以初始的线形为基础进行精确平衡分析,经多次迭代计算出结果(迭代次数越多,对悬链线的索单元分析越精确),并确定成桥线形。
2 工程算例
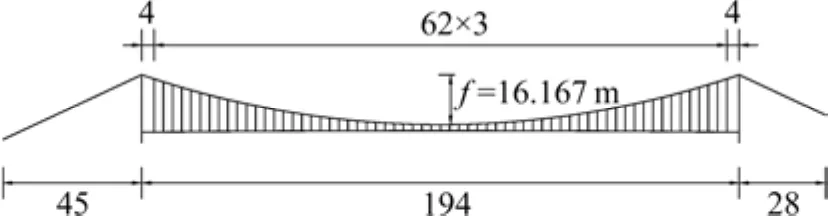
某桥为一跨地锚式玻璃悬索人行桥,其立面布置如图7所示。该桥的参数为:全跨194 m,吊杆间距(4+62×3+4) m,加劲梁自重3.552 kN/m,主缆的单位长度重1.223 kN/m,吊杆的单位长度重0.025 kN/m,垂度16.167 m。
2.1 由抛物线法和悬链线法计算主缆坐标
采用Matlab软件,由抛物线法和分段悬链线法计算主缆坐标。对 Matlab软件进行了编制详细程序。以各种荷载、吊杆间距和跨中垂度等作为已知量,输入各种初始参数。以主缆成桥坐标和空缆坐标作为未知量进行数值迭代,计算结果见表1。
设主缆水平力为 H1;竖直力为 V1。计算流程为:输入悬索桥初始参数→假定H1和V1的初值→程序计算→求解H1和V1→判定是否满足收敛条件→满足→返回H1和V1→由H1和V1计算各索段的吊索坐标→输出结果。如果判定不满足收敛条件,则对 H1和 V1进行修正后,返回第一步进行重新计算。
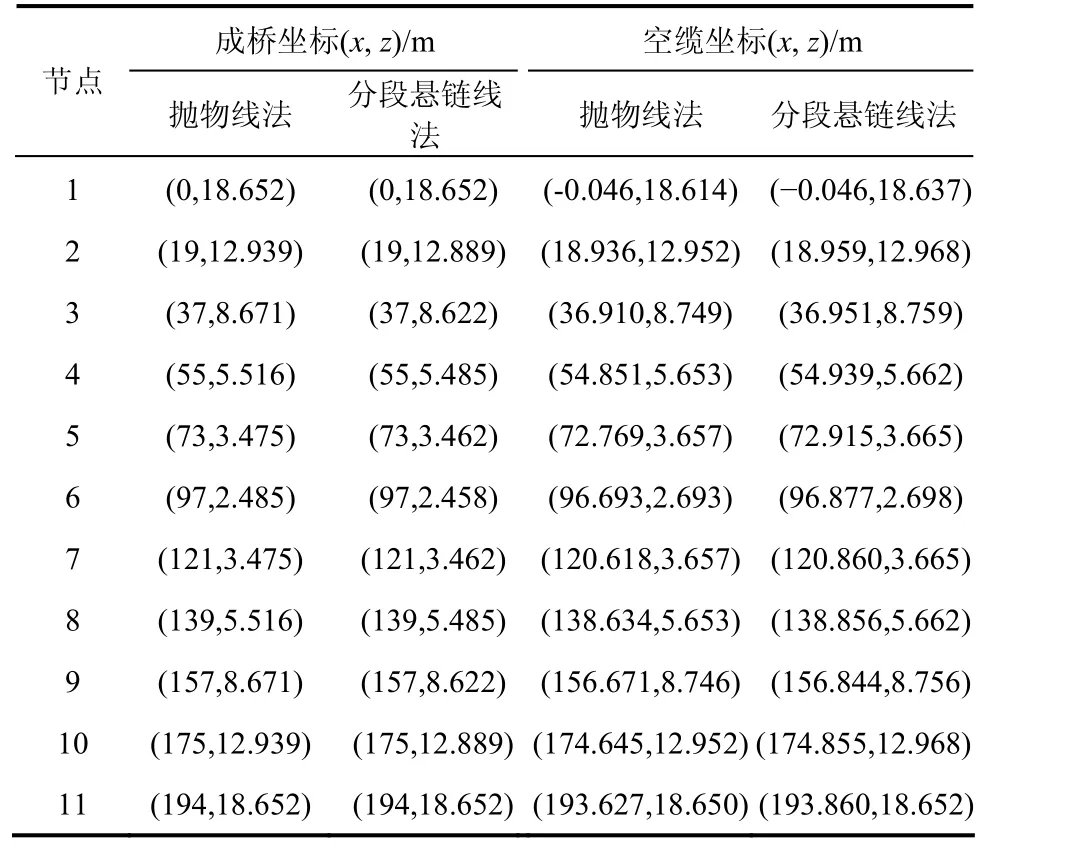
表1 主缆线形坐标Table 1 Final line shape of the main cable coordinates
2.2 由节线法计算主缆坐标
在用节点法计算地锚式悬索桥的形状时,把加劲梁上的均布荷载看成加载在吊杆下端的集中荷载,如图8(a)所示。经计算得:3 m段跨中集中荷载为5.538 kN;4 m段跨中集中荷载为5.644 kN。
计算水平张力Tx时,地锚式悬索桥的受力可简化为一根简支梁,如图8(b)所示。A点的支反力为168.148 kN;垂点C处的弯矩MC为8 352.904 kN·m。

利用水平张力和主塔反力就可以计算出第一根吊杆和主缆连接的节点左边的h1。设塔顶节点竖向力为RA,主塔节点受力如图8(c)所示。

主塔旁第一根吊杆上端节点z坐标为17.35。

图8 荷载布置Fig. 8 Load layout diagram
第二根吊杆上端节点的Z坐标是通过第一根吊杆上端节点的平衡条件来计算的。第二节点受力如图8(d)所示。同理,可以计算出所有主缆与吊杆相交节点的坐标。由计算出的主缆与吊杆相交节点坐标和吊杆与加劲梁的交点坐标就可以得到吊杆长度,相应的节点与节点之间的主缆长度也可通过主缆节点坐标得出来,进而计算出吊杆的自重,重新求得一个吊杆的单位自重。将吊杆的单位自重进行反复的迭代,最终求出收敛的主缆坐标。采用Midas/Civil 2019进行迭代求解,通常设定迭代的计算范数值小于0.01,则认定结果收敛。
在节线法计算主缆线形的过程中,模型的初始平衡状态并非精确平衡,仍会产生小位移和不平衡力,需要后期进行边界条件调整、索鞍模拟来消除,直到位移接近于0 m。只有进行反复迭代和精确平衡状态分析,主缆线形才会与工程实际接近。
采用Midas/Civil 2019建立的模型如图9所示。主缆共65个节点,64个单元。先将该模型做初始平衡状态分析。在确定垂点组和节点组后,进行精确平衡状态分析,建立一次成桥施工阶段分析验证平衡,得出成桥线形。最后,定义倒拆施工阶段,进行倒拆工序,求空缆线形。当迭代次数为5次时,成桥状态和空缆状态的部分坐标见表 2。本算例中坐标原点位于主塔与加劲梁的交点处,成桥状态主缆线形如图10所示,本桥吊杆竖直,Z坐标即为吊杆的长度。

图9 悬索桥计算模型Fig. 9 The calculation model of suspension bridge

表2 主缆线形坐标Table 2 Final line shape of the main cable coordinate

图10 主缆最终线形Fig. 10 Final line shape of the main cable
3 结果分析
将利用3种方法计算出的成桥状态主缆坐标进行了比较,它们的节点坐标相差不大。节线法与抛物线法相比较,最大相对误差为0.47%,最小相对误差位0.28%。分段悬链线理论的假定符合悬索桥实际情况[13-14],可以解决吊杆拉力已知、加劲梁逐段衔接施工的问题,还可忽略主塔变位对主缆线形影响的主缆系统受力与线形计算的问题[15]。本研究采用分段悬链线方法对节线法进行了校验,使用基于节线法的Midas/Civil 2019软件,经过循环数值迭代,计算出的主缆坐标与用分段悬链线方法的结果相吻合。2种方法的成桥和空缆坐标相对误差在0.1%以内,那么计算出的有应力索长度和无应力索长度误差不会很大,而用抛物线法的误差最大,在文献[16]中也得到证明。
用节线法对地锚式悬索桥主缆线形进行非线性分析较准确,但也可能出现不收敛情况。这时,需要仔细检查边界条件和荷载,并分析控制数据等。
4 结论
传统抛物线方法计算过于粗略,对于大跨度的悬索桥分析并不适用。分段悬链线理论对于主缆的找形和主缆受力分析较为精确,同时也符合施工实际情况。但是,分段悬链线法计算复杂,在分析方法中较少采用。本研究以分段悬链线法对节线法进行了校验。
在主缆两端主塔顶的坐标、垂度、吊杆在加劲梁的连接节点位置及加劲梁上的荷载均为已知,在主缆张力的水平分量恒定不变的情况下,采用节点法计算主缆线形相对较为方便。采用 Midas/Civil 2019,基于节线法,对地锚式悬索桥进行了分析,得出的结论为:
1) 通过加劲梁、吊杆和主缆自重的平衡关系,用节线法确定主缆水平张力和主塔的反力,从而求得主缆节点坐标,确定主缆线形。
2) 将初始平衡求得的主缆线形坐标进行反复迭代,可计算出收敛的新坐标。迭代次数越多,坐标精度越高。迭代次数为5次时的计算精度与分段悬链线法一致,两者计算相对误差仅在0.1%以内。表明该方法准确。
3) 在采用Midas/Civil 2019计算初始平衡状态位移时,若出现有不为0 m的情况,必须调节模型的边界条件。对塔顶索鞍进行模拟,直至位移接近于 0 m时,该模型才真正处于平衡,计算结果才准确。
4) 初始平衡状态分析和精确平衡状态分析 2阶段都是用节线法计算的。使用该方法是成桥阶段和施工阶段做倒拆分析的前提,且能提高运营阶段的线性和非线性分析的工作效率。
确定地锚式悬索桥主缆线形的方法有多种,节线法是快速计算主缆方法之一,现已在工程实例中得到验证,该方法的使用对悬索体系桥梁的设计和施工具有一定的指导意义。

