高速公路交通事故后基于优化的强制换道研究
王正武,邹文竹,郝威
(长沙理工大学 交通运输工程学院,湖南 长沙 410114)
高速公路发生交通事故后,事故点上游车辆需换道来避开事故车道。目前,已有不少学者研究了换道问题。换道问题分为换道决策研究、换道模型研究及换道轨迹研究等。换道决策的内容包括:意图产生、目标车道选择及换道条件评估等。在换道决策研究方面, Kanaris[1]等人针对自动高速公路系统中车辆换道问题,提出了基于最小安全距离换道条件的评估方法。Talebpour[2]等人提出了车联网环境下,基于博弈论的换道决策模型。Meng[3]等人引入结构平衡理论,考虑车辆间的相互影响,建立了滚动时域控制的换道博弈模型。Nilsson[4]等人按是否换道、何时换道及如何换道3步,分析了自动驾驶车辆的换道决策问题。Hidas[5]为智能交通系统提出了强制换道和协同换道模型,并通过仿真实验,验证了拥挤情况下强制换道和协同换道的可行性。李玉洁[6]等人分析了施工区不同换道点道路交通状态的变化特性和最佳换道点的选择问题。李珣[7]等人利用威胁度函数,刻画了多车辆间的相互关系,建立了车、路协同环境下考虑局部区域车辆状态的协同换道规则模型。李娟[8-9]等人分别建立了自由换道、强制换道及协作换道3种换道方式的换道模型和跟随车与换道车之间的最小安全距离模型。吴江玲[10-11]等人建立高速公路强制换道持续时间的生存模型,分析了车辆类型和换道时间对换道耗时的影响。在换道轨迹研究方面,现有研究以几何曲线法为主。Nelson[12]为构建曲率连续的自动车辆导引轨迹,首创了多项式轨迹曲线方法。Piazzi[13]等人提出五次多项式轨迹规划方法,保证了自动驾驶车辆轨迹的平坦性和可执行性。游峰[14]等人考虑车辆间的相互影响,基于换道安全,提出了面向无人驾驶车辆的协同换道轨迹规划方法。已有的研究中,多数均假设车辆匀速换道,很少考虑减速换道的情况,且都是研究的单车辆换道行为。实际上,若目标车道车头间距合适,后车也可能跟随前车一起换道。大多数车辆换道是基于规则选择可行换道点进行换道,很少基于优化的方法来确定换道点。而且,在基于规则选择换道点时,很少考虑前车换道点的选择对上游车辆运行状况和换道点的影响。因此,作者拟基于车流波理论,确定高速公路交通事故影响区及目标车道上不同位置车辆的运行速度,以换道距离和最小安全距离等为约束条件,构建跟车换道可行点模型;以换道车辆纵向行驶距离之和最小为目标,建立车联网环境下换道可行点及方式的协调优化选择模型,以提高交通事故影响区的运行效率。
1 基于优化的换道模型
1.1 问题描述
高速公路上交通事故发生后,事故点可通行的车道数减少,事故点上游的部分车辆需强制换道。本研究以双向四车道高速公路因交通事故导致一个车道封闭的情况(如图 1所示)为例。设事故发生时刻为t0,恢复通车时刻为tf,t0至tf时间内事故路段上单向交通量为 Q(忽略事故路段交通量的波动);在t0时刻,事故点上游车辆运行速度均为v0,事故车道上车辆i的位置为[Xi(t0),Yi(t0)],目标车道上车辆 k的位置为[Xk(t0),Yk(t0)],事故影响区长度为S。

图1 事故路段车辆换道场景Fig. 1 Lane-changing scene on accident link
在车联网环境下,高速公路交通事故影响区车辆换道的问题可描述为:根据初始时刻事故路段所有车辆的位置和速度信息,确定t0至tf时间内任意时刻事故影响区各位置车辆的运行速度,计算事故车道上各位置车辆的跟车换道可行点,并以换道车辆纵向行驶距离之和最小为目标进行优化,确定事故车道上各车辆的换道点、换道方式(单车换道或跟车换道,图1中事故车道上车辆1和2就是跟车换道、车辆i+2、i+3就是单车换道)。
1.2 影响区模型
交通事故发生后,事故点上游车辆基于车联网获取实时信息,目标车道上的车辆将采取制动措施,从而形成车流波并向上游传播,初始时刻t0至结束时刻tf时间段Δf内传播的距离就是事故影响区长度S。

式中:vw是波速;CII为事故点要求的二级服务水平下的最大服务交通量(也可以取为尽快疏散交通需保持的最大交通量或其他值);KII为CII所对应的密度;K为事故开始时事故车道上车流密度,K= 0.5Q/ v0。
设目标车道的车辆均以减速度a匀减速到最佳车速vII后保持匀速行驶,直到通过事故点,t0至tf时间内任意时刻t影响区内车辆k的运行速度为:
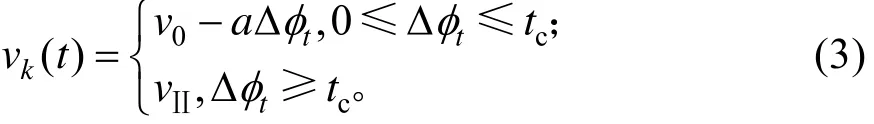
式中:tφΔ为车辆从t0时刻到t时刻行驶的时间;tc为减速时间;vII为最佳车速。
陈凯贤[15-16]等人分别针对高速公路事故影响区域和高速公路施工区的车辆速度限制进行了研究。在本研究中,为了保证车辆的最大通行效率,最佳车速vII为二级服务水平下密度KII时对应的速度。减速时间的计算式为:

1.3 跟车换道可行点模型
事故发生后,设事故车道上的车辆在换道前仍以初始速度v0匀速前行,在前行过程中,不断寻找换道可行点,在选择的换道可行点以纵向减速度ax进行减速换道,达到目标车道的运行车速vII后跟随目标车道上的前车匀速行驶。换道可行点包括单车换道可行点和跟车换道可行点2类。在单车换道可行点的基础上,基于最小安全距离约束判断是否能后续m辆车跟车换道。
设车辆i选择换道点y在t时刻完成换道后目标车道上的前、后车分别为k和k+1,车辆i的单车换道可行点集合为Ri,则Ri可表示为:

式中:riy为车辆i的换道点y的横坐标;td为车辆换道所需的时间;ti为换道车辆i在事故车道上以初始速度 v0匀速行驶到达事故点的最长时间;Δx为车辆i换道过程中行驶的纵向距离;Ls为车辆速度vⅡ时目标车道上车辆间的最小安全距离。
式(5)表示单车换道可行集应满足的约束分别为:车辆i从换道点y开始换道,完成换道后与目标车道上前、后车k和k+1的距离应满足最小安全距离;车辆i的换道点y应在最晚换道点之前;车辆i换道应该在td到ti时间段内完成。
式(6)表示车辆i在t时刻能够完成换道时的可行换道点位置;式(7)表示换道所需的时间即换道车辆完成横向移动所需的时间;式(8)保证车辆在时间段ti内完成换道,即在到达事故点之前完成换道;式(9)表示车辆 i换道所行驶的纵向距离;式(10)表示目标车道上车辆k在任意t时刻的纵向位置。
在车辆i和车辆i-1单车换道可行点集合分别为Ri和Ri-1的基础上,判断哪些可行点可进行跟车换道的可行点。若车辆i跟随前车i-1换道,则车辆i的跟车换道可行点的集合为:
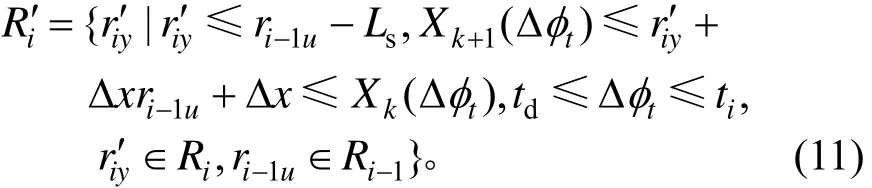
式中:iyr′为车辆i的换道点y的横坐标;1iur-′为车辆i-1选择换道点u的横坐标位置开始换道。
式(11)表示车辆 i跟车换道可行集应满足的约束分别为:车辆i与前车i-1之间换道点的距离应满足最小安全距离;完成换道后,车辆i与前车i-1进入目标车道,且处于相同的车辆k和k+1之间。车辆i换道应该在td到ti时间段内完成。
1.4 跟车可行点的优化选择模型
高速公路上发生交通事故之后,若事故点上游车辆换道不及时,将可能导致二次事故的发生,进而加剧交通拥堵。为避免发生二次事故,处于事故点上游的车辆应尽快换道至目标车道以远离事故点。因此,本研究目标是使影响区内所有换道车辆在事故发生时刻至完成换道时刻所行驶的纵向距离之和最短,建立的目标函数为:
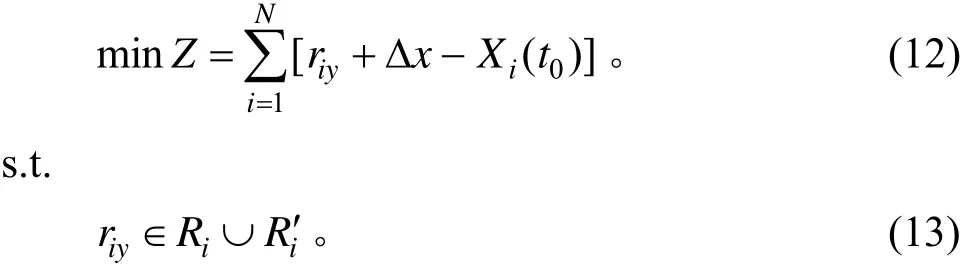
式(12)表示影响区上所有需要强制换道N辆车完成换道时所行驶的纵向距离之和最短;式(13)表示换道可行点应属于单车换道可行点或跟车换道可行点。
通过这些优化模型,可同时确定所有换道车辆最优的换道点组合和换道方式组合。
2 求解流程
根据强制换道模型的特点,在单向双车道高速公路发生交通事故的情况下,以事故车道上事故区上游影响区内的车所有辆为研究对象,其求解步骤为:
1) 输入初始速度、车流量、直线行驶减速度及换道纵向减速度等参数,计算事故影响区域长度、最佳车速、需要强制换道的车辆数、减速至最佳车速的时间及换道的时间等参数。
2) 计算需要强制换道的每一辆车在任意时刻完成换道时的纵向位置。若满足与前、后车的最小安全距离,则将该时刻对应的换道点位置放入集合Ri中。
3) 若车辆完成换道,则更新车辆位置。在单车换道的基础上,根据式(11)判断车辆是否能进行跟车换道,得出车辆的跟车换道点的集合iR′。
4) 利用整数规划的方法,求出目标函数的最优解。
5) 输出每一辆车的换道点位置及换道方式。
6) 更改初始参数设置,重复步骤1)~5)。
3 算例分析
有一条双向4车道高速公路,因交通事故导致一个车道封闭的情况,如图1所示。设计了2个实验来验证该方法的有效性,分析初始交通量和车速对换道方式、换道点的影响。①实验 1,仅变化初始交通量Q,分析初始交通量对换道方式、换道车辆平均纵向距离的影响。②实验 2,仅变化初始速度v0,分析初始速度对换道方式、换道车辆平均纵向距离的影响。
3.1 参数说明
针对实验 1,2,共设计了 5组实验参数。利用式(1),(3),(5)和(8)及交通流3个基本参数之间的关系等,得到影响区长度S和需强制换道的车辆数N等的计算值。初始流量可反映车辆间距,初始速度可反映车辆间最小安全距离。因此,通过初始流量和初始速度2个参数来反映在不同条件下对车辆换道点、换道方式的影响。
在实验1中,第一组设置已知参数为:初始流量1 600辆/h,二级服务水平下的最大服务交通量1 400辆/h,初始速度25.0 m/s,直线行驶减速度2 m/s2,换道纵向减速度1.5 m/s2,第二、三组的初始速度固定不变,初始流量分别为1 700和1 800辆/h。在实验2中,第四、五组的初始流量固定不变,初始速度分别为22.2和27.8 m/s。
通过计算可得,最佳车速为18.5 m/s固定不变。在实验1中,由于只有初始车流量的变化,随着车流量的增加,事故影响区的长度会增加,分别为8 300,13 000和18 200 m;需要强制换道的车辆也会增加,分别为73,123和182辆;直线行驶减速时间为3.2 s,换道时间4.3 s。在实验2中,由于只有初始速度的变化,随着初始速度的增加,事故影响区的长度会缩短,分别为9 100,8 300和7 700 m;需要强制换道的车辆也会减少,分别为91,73和62辆;直线行驶减速时间则会增加,分别为1.9,3.2和4.6 s;换道时间也会增加,分别为2.5,4.3和6.2 s。
3.2 结果分析
利用 Matlab语言编程,求解所构建的优化模型,输出车辆的换道起始点和换道方式。实验1结果表明:随着初始流量的增加,车辆跟车换道的概率分别为 36.9%,28.4%和 36.8%。流量适中时,车辆跟车换道的概率更低。实验2结果表明:随着初始速度的增加,车辆跟车换道概率也随之增加,分别为7%,36.9%和38.7%。因此,在流量较低或较高、以及车速较高时,车辆更应选择跟车换道来提高换道的效率,从而尽快远离事故影响区。
2个实验 5组数据对应的计算结果分别见表1,2。从表1,2中可以看出:①利用该模型,能优化并确定换道车辆的换道点、换道方式,表明了该方法的有效性。②初始流量和初始速度的变化导致换道车辆的换道点发生了显著变化,导致跟车换道的车辆数、跟车换道的车辆组合也发生了较大的变化,初始流量和初始速度对换道点、换道方式均有显著影响。③实验1中,初始流量从1 600辆/h增加到1 700辆/h再增加到1 800辆/h时,影响区内所有换道车辆在事故发生时刻至完成换道时刻所行驶的纵向距离之和Z增加了144.2%,Z对初始流量的弹性从11.19变化到7.43。表明:换道车辆纵向行驶距离之和与初始流量正相关,而且随着初始流量的增加,换道车辆纵向行驶距离之和的变化率将越来越小。换道车辆的平均纵向行驶距离从增加 1.0%到减少 2.9%,相对于初始流量的弹性从0.16变化到-0.49。表明:增加初始流量,换道车辆的平均纵向行驶距离是增是减不定,但换道车辆纵向行驶距离之和的变化率将越来越大。跟车换道车辆比例从减少23.9%到增加35.6%,跟车换道车辆比例对初始流量的弹性从-3.83变化到6.05。表明:增加初始流量,跟车换道车辆比例是增是减不定,但换道车辆纵向行驶距离之和的变化率将越来越大。④实验2中,初始速度从22.2m/s增加到25m/s再增加到27.8m/s时,影响区内所有换道车辆在事故发生时刻至完成换道时刻所行驶的纵向距离之和Z从减少18.1%到增加3.3%,Z对初始速度的弹性从-1.43变化到 0.30。表明:增加初始速度,换道车辆纵向行驶距离之和是增是减不定,但换道车辆纵向行驶距离之和的变化率将越来越小。换道车辆的平均纵向行驶距离增加了 24.2%,z对初始速度的弹性从0.16变化到1.95。表明:换道车辆的平均纵向行驶距离与初始速度正相关,而且随着初始速度的增加,换道车辆的平均纵向行驶距离的变化率将越来越大。跟车换道车辆比例从增加481.9%到增加1.0%,跟车换道车辆比例对初始速度的弹性从38.2变化到0.09。表明:增加初始速度,跟车换道车辆比例也会增加,但换道车辆纵向行驶距离之和的变化率越来越小。

表1 实验1的计算结果Table 1 Calculation result of Experiment 1

表2 实验2的计算结果Table 2 Calculation result of Experiment 2
4 结语
基于最小安全间距和换道距离等,构建了车联网环境下高速公路发生交通事故后优化车道的强制换道模型,获取了优化的换道点和换道方式,得到的结论为:
1) 利用模型优化确定了换道车辆的换道点和换道方式,并表明该方法的有效性。
2) 初始流量和初始速度对换道车辆的换道方式、换道点均存在显著影响。换道车辆纵向行驶距离之和与初始流量正相关,换道车辆的平均纵向行驶距离、跟车换道车辆比例均与初始速度正相关。增加初始流量,不能确定换道车辆的平均纵向行驶距离和跟车换道车辆比例的增减。同样,增加初始速度,也能不确定换道车辆纵向行驶距离之和的增加。
后续的研究将分析多因素共同作用对换道方式和换道点的影响。

