大口径长输管道整体下沟过程的有限元校核分析

张宏志

大庆油田工程建设有限公司安装公司，黑龙江大庆 163416

随着我国成品油、天然气管道网络结构战略布局的推进，未来十年油气长输管道将迎来新的建设高峰期。长输管道的沟上焊接、整体下沟技术，以其高效、安全、环保等特点逐渐取代了沟下焊接作业的传统施工方法。但是整体下沟技术仍存在着应用主观性强、管道易产生残余变形等施工难点，尤其是大口径管道整体下沟施工，其难度更大。大口径管道整体下沟的关键问题是大变形、大位移、大挠度，其容易导致管道在横向、竖向产生较大变化，从而给管道造成不同程度的损伤。

本文针对俄气东输管道工程中规格为D1422mm×21.4 mm、管材为X80钢、管沟深度为4 m的大口径管道的整体下沟技术进行研究。对管道的起吊进行受力分析，根据吊管机的工况，合理布置下沟位置，分析校核管道整体下沟的技术方案，找到管道整体下沟过程中产生的最大应力，并将其设置为施工关键点加以控制，优化了大口径管道整体下沟的施工工序，保证了管道整体下沟过程中不损坏母材，从而提高了大口径管道整体下沟的准确性、安全性和可靠性。

1 起吊管道受力分析

大口径管道下沟过程采用吊管机将管道吊起，由于存在着起吊过高或吊点过少而造成管体应力超过许用应力的问题，因此需要对管道吊起时的受力进行分析，即需要计算出管道的最大起吊高度h、吊管机负荷P、管道离地长度L的数值[1]（见图1），以指导管道的施工。

管道吊点离开地面的高度最大值h：

图1 管道起吊情况示意

吊装设备负荷P：

管道离地面部分的1/2长度L：

式中：h为管道起吊高度，m； [σ]为管材许用应力，Pa；I为管道轴惯性矩，m4；D为管道外径，m；q为管道单位长度重度，N/m；E为管材弹性模量，Pa；P为吊装设备的负荷，N；L为离地管道长度的一半，m。

2 管道整体下沟最短区段长度的确定

将管道分成两个区段OA、AB。O点管墩的高度为0.3 m，A点距地面高度1 m，OA为管道第一位置点抬起的长度，AB为管道可下入沟底的最短长度，此右边AB区段的管道由地面1 m高度降至-4 m的沟底，见图2。

图2 管道下沟区段的最短长度AB

管道的极限弯曲曲率半径[2]为：

式中：RS为管道弯曲最小曲率半径，m；Rσ为管道弯曲最大曲率半径，m；σs为管道屈曲强度，Pa。

代入相关参数，则得：

根据图2和式（3）可以算出，可下入沟底的最短管道长度（AB区段）为12 m。而实际管道整体下沟的总长度为208 m。

3 确定管道整体下沟的吊管机配置方案

根据吊管机的性能参数、管道极限弯曲曲率半径、管道与管沟中心的水平距离等，确定吊管机的配置数量和初始站位[3]。表1中对整条管道区段重新进行了划分，各点位置见图3。

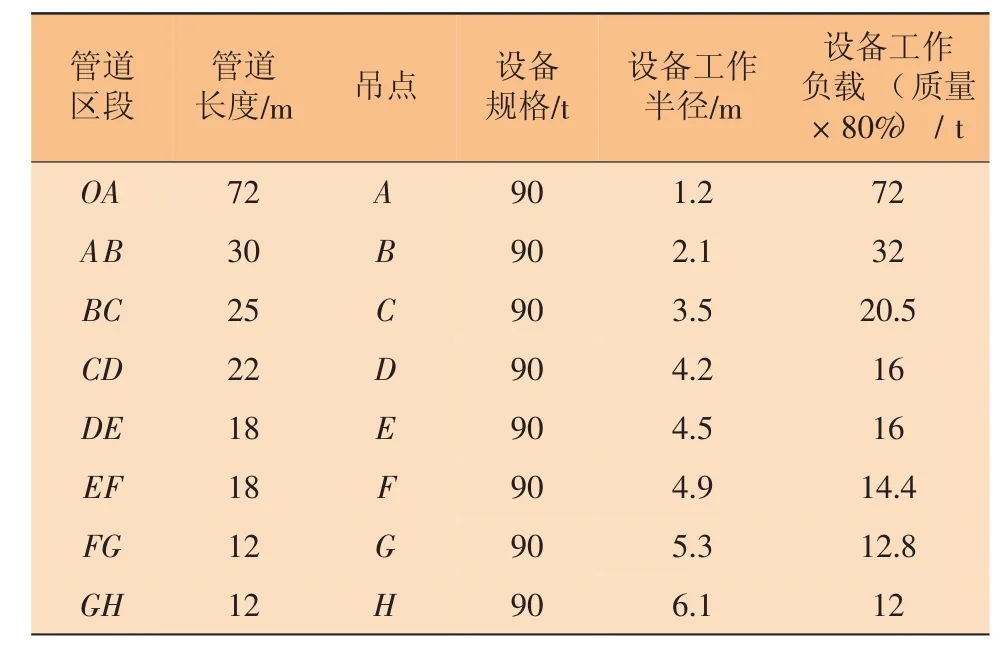
表1 吊管机配置计算

图3 吊管机配置

根据表1吊管机的配置，当位于管道72 m位置时，管道离地高度为0.7 m，吊装质量为28.3 t，满足90 t吊管机负荷能力80%的要求；当位于管道72～208 m区段时，此区段的设备布置原则是管段重量小于吊管机在工作半径下负荷能力的90%，根据此原则，依次布置了B、C、D、E、F、G、H等7个吊点，共计8个吊点，见图3。

4 管道挠度曲线的拟合

由于大口径管道长度跨度大，采用多吊点提升，因此，通过采用多项式插值函数拟合管道挠度曲线，进而建立多点提升的力学模型，由此计算出各种提升状态下的变形和内力，从而实现对施工方案的力学校核。管道在端部和中部的n个点上受到铅直向上的提升力作用，各受力点产生铅直向上的起吊高度；提升点间距的合理布置及管道长度方向均匀分布的自重，使得管道产生曲率不大的弯曲变形[4]。

4.1 插值挠度曲线

插值挠度曲线是与修正荷载集度qi有关的四次多项式，i+1段的插值函数yi+1（x）和i段的插值函数yi（x） 在考虑x=ai处的连续条件后得到下式：

对于任意一段插值函数可以确定出下式：

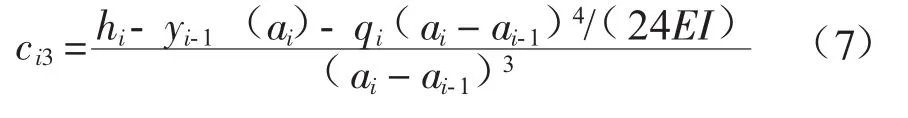
其中：i=2，3，…，n

4.2 水平状态y和下落状态z的挠度拟合曲线

水平状态y和下落状态z的拟合曲线见式（8）、（9），其图像见图4。

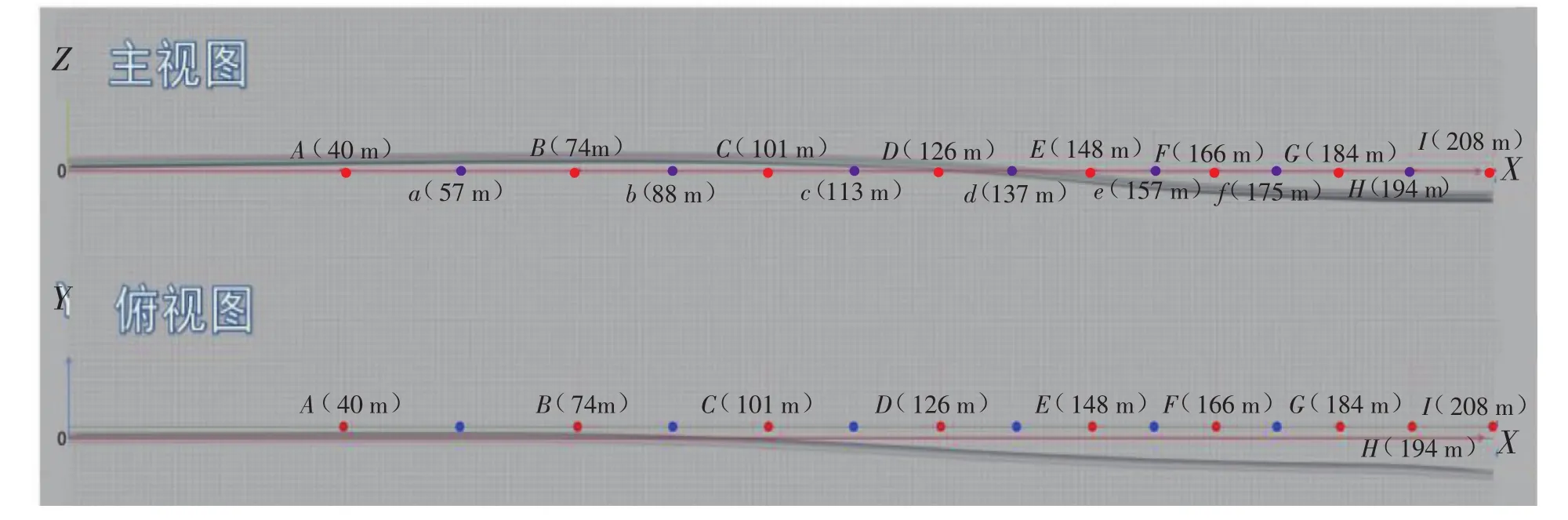
图4 挠度拟合曲线图形

5 长输管道整体下沟的有限元校核

为确保管道下沟安全，对管道整体下沟进行非线性有限元分析，有限元分析校核分为管道起吊、平移至管沟顶部、垂直下落至沟底三个阶段。校核管道变形应力、吊管机的间距、起吊高度和吊装能力是否满足管道材质要求和施工要求。

俄气东输管道工程管径D1 422 mm，壁厚21.4 mm，管材X80钢，弹性模量205 GPa，泊松比0.3，管道密度7 860 kg/m3，屈服强度555 MPa。管道整体下沟过程中主要承受自重载荷和吊管机的提升力。管道计算总长208 m，布置8个吊点，管道弯曲曲率半径R为700D。管道下沟前的状态如图5所示。

5.1 管道起吊过程

根据挠度拟合曲线公式，初始管道底部距离地面0.7 m，大口径管道穿过吊装带由吊管机起吊。采用有限元分析软件Abaqus[5]对管道起吊过程进行分析，得到管道起吊时的受力如图6所示，管道起吊时的位移（挠度拟合曲线位移值）如图7所示。

管道起吊过程中，最大的应力出现在第1个吊点A前段，为141.7 MPa，小于X80钢管的许用应力。该吊点距离地面0.7 m，其余各吊点提升距离都小一点，应力比较小。每个吊点上管道的位移值（挠度拟合曲线位移值）为0.7 m，与实际施工工况相符。

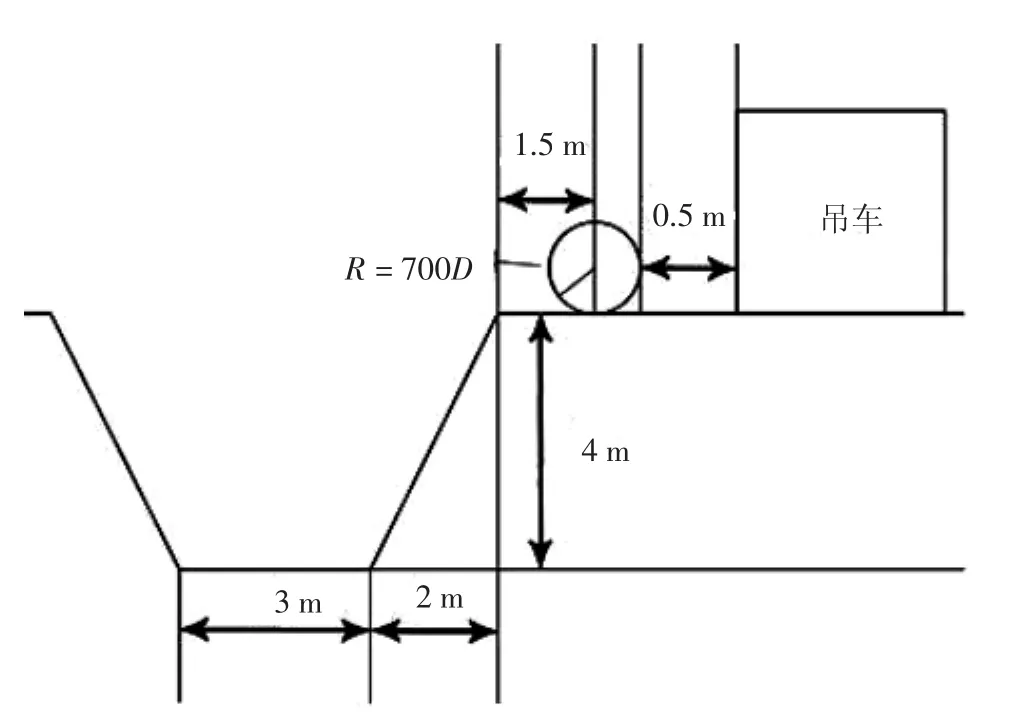
图5 管道下沟前的状态

图6 管道起吊应力图/Pa

图7 管道起吊位移图/m

5.2 管道水平转动至管沟顶部过程

管道中心距离管沟中心为4.927 m，管道水平转动至管沟顶部过程中的受力如图8所示，管道水平转动至管沟顶部的位移（挠度拟合曲线位移值）如图9所示。

图8 管道水平转动至管沟顶部的应力/Pa

图9 管道水平转动至管沟顶部的位移/m

管道水平转动至管沟顶部过程中，管道端部的位移值（挠度拟合曲线位移值）是5.049 m，第8个吊点的管道的位移值为4.927 m，其余各点与挠度拟合曲线对应。计算结果显示，最大的应力出现在第7个吊点G，该处产生了应力集中。其主要原因是为了实现此管段与沟底的走向一致，挠度拟合曲线在此吊点的位移值较大。因此在实际施工中应减少此吊点的作用力，可通过允许管道有限滑移至沟底来实现。

5.3 垂直下落至管沟底的过程

管沟深度为4 m，管道在自重的载荷下缓慢下落，控制管道的下落速度，管道首端下落到沟底时计算完成。在下落初始时，第1个吊点固定，下落完成后观察管道的应力分布。管道垂直下落至管沟底的应力如图10所示，管道垂直下落至管沟底的位移（挠度拟合曲线位移值）如图11所示。

图10 管道垂直下落至管沟底的应力图/Pa

图11 管道垂直下落至管沟底的位移图/m

管道从管沟顶部垂直下落到沟底时，管道前端垂直方向的位移值（挠度拟合曲线位移值），从最初的0.727 9 m缓慢下降到-4.16 m，第8个吊点H的下降距离是-4 m。最大应力出现在第7个吊点G位置，接近X80钢管的屈服强度，其主要原因是此管段在水平弯曲时的应力比较高，造成下落的时候应力比较集中。实际下沟过程中不会强调管道轴线精准对中，不会施加很大水平弯曲力矩，所以管道在下沟中应力不会超出管道许用应力。

6 施工方案的工程应用

通过对大口径长输管道整体下沟的有限元分析校核，揭示出管道整体下沟过程中应力集中的部位，该研究成果可用于施工过程中吊管机的优化配置和监督控制。本文技术成果已应用于俄气东输管道工程的管道整体下沟施工中，设备在吊起、锁紧、扩展、下落等操作中，设备负荷始终控制在计算负荷内，实现了大口径管道整体下沟的安全和可操作。该技术的工程应用效果见图12。

图12 工程应用效果

7 结束语

本文应用非线性有限元分析法研究了俄气东输管道工程中D1 422 mm×21.4 mm大口径管道整体下沟施工方案的可行性。通过对该管道整体下沟过程进行应力、应变校核，给出了保证管道下沟不发生变形损坏的施工方案参数。该技术的实施提高了长输管道整体下沟的安全性、可靠性，具有良好的应用效果和推广前景。