“分数的初步认识”中的“初步”与“认识”

陈士文　陆克荣

摘要：“分数的初步认识”第一课时的教学，可让学生通过分一分认识到分数来自平均分，是一种发明与创造;通过折一折、涂一涂认识到分数是一个（数）量，是有大小的;通过写一写认识到分数和整数是相关联的。

关键词：分数的初步认识 认识几分之一 平均分 数量 整数

数学学习中，从整数（实际是自然数）到分数，是学生经历的第一次“数系的扩充”。从整数到分数的跨越，本质上是从离散量到连续量的跨越、从（一一对应）数数到（分割后用单位）测量的跨越。学生刚开始学习分数，无论对分数的意义和表示，还是比较和计算，都会感到困难。对此，苏教版小学数学教材以螺旋上升的方式，分别在三年级上册、三年级下册、五年级下册、六年级上册，编排了《分数的初步认识（一）》《分数的初步认识（二）》《分数的意义和性质》《分数的加法和减法》《分数乘法》《分数除法》等单元，引导学生逐步学习，降低学习难度。

但是，在实际教学中，教师经常感到三年级“分数的初步认识”，尤其是第一课时《认识几分之一》的教学不太好把握。下面，围绕“初步”和“认识”这两个关键词，谈一谈《认识几分之一》的教学该如何定位和实施。

一、关于“初步”——教学定位

教师可以从分数的产生、分数的形态、分数与整数的关联三个方面思考“初步”体现在哪里。

（一）分数与平均分

“分数的初步认识”，应该让学生感受到分数是因生活的需要而产生的：在分一分的过程中，因为整数不好表达小于1的物体（不足1的部分），所以，分数产生了。不必上升到分数是因生产的需要或数学自身的发展而出现的——当然，平均分的过程无形中蕴含了分数与除法的关系。此外，对于“分数是建立在平均分基础上的”这一本质，还应该让学生充分认识各种平均分，尤其是一些看上去不是但实际上是的平均分（所分的各部分不能完全重合，但从度量的角度看是一样大或多的）。

（二）分数的量与率

整数是直接从具体事物中抽象出来的。分数是先“分”而后得的“数”，比整数更抽象。整数的认识是从一个个具体的量开始的。比如，从一朵花、一个苹果、一支笔、一本书等，逐步形成数字“1”的概念。因此，分数的认识如果也从“量”开始，则学生容易接受。即：在分数后面缀上单位，如1/2个、1/3块、1/5杯等，学生容易理解。因此，“分数的初步认识”，不必涉及“率”。

（三）分数与整数

分数认识是整数认识的扩展，分数和整数始终在一起。比如，分数3/4可看作平均分整数1为4份，取其中的3份;也可看作平均分整数3为4份，取其中的1份。即：3/4=1/4×3或3/4=3÷4。3/4的背后是整数1或3。因此，“分数的初步认识”，要以整数为基础，联通到整数单位，不能孤立地认识，也不必过多地应用（解决实际问题）。

二、关于“认识”——教学实施

知道了“初步”认识的内容及其程度后，就要思考如何“认识”。我们通过教学片段来说明。

（一）分一分，发现分数来自平均分

师同学们，今天这节课我们认识新的数。新的数在哪里呢？（出示图片）这是一块饼，小红想一个人吃，那她可以吃几块饼？

生1块。

师这时，小亮来了。好东西要和朋友分享，怎么分享呢？

生从中间分开，一人吃一半。

师为什么要从中间分开呢？

生两份一样大，分得公平。

师这种分法叫作怎么分？

生平均分。

師这样每人吃几块？

生半块。

生二分之一块。

师半块就是二分之一块。一块饼平均分成两份，其中的一份就是二分之一块。这个数你以前学过吗？

生没有。

师这就是今天我们要认识的新的数，叫作分数。谁听明白二分之一块的意思了？请说一说。

（学生说。）

师如果是一大一小这样分的，还能说分了二分之一块吗？

生不能。

师分的方式是平均分。（介绍分数各部分的名称：分子、分母、分数线……然后出示图片）巧克力、饮料、红纸条为什么都用分数，而不用以前认识的1、2这样的整数来表示？

生巧克力没有1块大，饮料不满1杯，红纸条没有1米长，我们用分数1/3、1/5、1/6来表示。

师（出示图1）图中阴影部分为什么能用分数表示？它好像不是平均分。

生（思考片刻）它是平均分。把大正方形横竖对折，分成四个小正方形，每个小正方形中，阴影部分和空白部分都一样大，是平均分。

师非常好！大家要特别注意那些看上去不像平均分的平均分哦。以往学的是整数，今天整数不好表达了，就产生了新的数。分数是在“分”的过程中出现的。

借助饼、巧克力、饮料、纸条等不同素材，引导学生在分一分中感悟：分数是在生活表达遇到困难时人们的一种发明与创造。此处，既要让学生知道知识（分数各部分的名称），又要让学生增长见识与智慧（分数的发明与创造）。

（二）折一折、涂一涂，发现分数有大小

师刚才我们分一分，找到了今天要认识的新的数。现在请同学们拿出一张正方形纸，折一折、涂一涂，表示出分数。

（学生活动。）

师（出示下页图2）谁愿意说一说你是怎么做的？

生把纸对折，涂上一份。

师对折和我们黑板上的哪个词意思一样？

生平均分。

师有同学表示出了1/4。说说看。

生把纸对折，再对折，涂上一份。

师如果老师用同样的方法去涂1/2和1/4，哪个涂得快？

生1/4涂得快，因为1/4小。

师还有谁表示的分数让我们涂得更快？

生1/8。

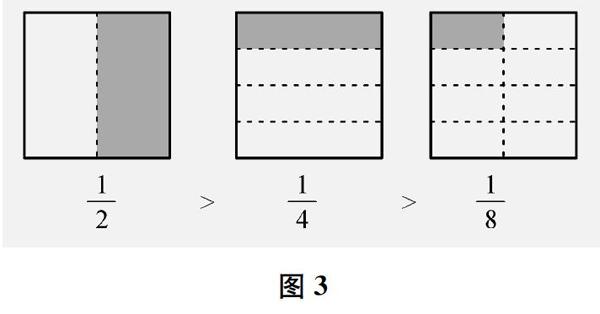
师（出示图3）我把这些分数展示在屏幕上，你有什么发现？

生我们涂的时候，感觉分数是有大小的。

师你能想一想为什么分数有大小吗？

生平均分的份数不同。分得越多，每一份越小，分数也就越小。

师以前我们认识的整数有大小吗？8和4相比哪个大？1/8和1/4呢？

生8大，1/4大。

师分数和整数都有大小，不过比较的方法有些不同，你们能体会到吗？

直观地看可以发现分数的大小，动手去涂可以感受分数的大小。但仅仅这样“认识”是不够的，还应该从平均分的份数多少上说明分数的大小，以及自然地联系到整数的大小比较，发现其与分数大小比较的不同之处。

（三）写一写，发现分数和整数相关联

师我们分过了，也涂过了，下面来写一写吧。（出示图4）这是一块黑板，用1来表示。（同步指图）其中这一块是“科学天地”，这一块是“艺术园地”，剩下的是“智慧园地”。你在上面看到了哪些分数，在作业纸上写一写。

生（展示）1/2、1/4、1/4。

师一块黑板是整数1，同学们在图中找到了三个分数，真厉害！（出示图5）这幅图，你能写出哪些整数？

生1、3，1、9。

师你还能找到分数吗？

生1/3、1/9。

师我们今天学的是新的数——分数。在图上，我们看到了分数的分子、分母所表示的整数，说明分数和整数是有关联的。

通常的看图写分数只是一般技能。而此处的看图写分数具有整体的视野：既写分数，又写整数，在写的过程中，感悟分数与整数的联系。

参考文献：

[1] 远山启.数学与生活（修订版）[M].吕砚山，李诵雪，马杰，等译.北京：人民邮电出版社，2014.