基于加窗插值谐波分析法的容性设备介损角测量研究

李杰，杨志华，王应芬，朱胤宇，李家保，隋永浩，马学林

（云南电网责任有限公司红河供电局，云南红河654400）

0 前言

随着电力系统不断朝着“一特四大”发展，其安全稳定运行对国家经济发展和人民生活的影响越来越凸显。有学者曾对我国“九五”期间发生的电网事故进行过统计，数据显示：电力设备的绝缘击穿是致使设备发生故障甚至引发安全事故的首要原因，占比高达23.1%[1]。容性电力设备在电力系统中占有较大比例，其绝缘故障不仅关系到变电站的安全运行，还会影响工作人员甚至整个系统的安全。因此，电网运行部门对容性设备开展绝缘在线监测具有重要的工程实践意义，其中介损测量是绝缘监测的重点内容。

介质损耗的监测方法在原理上可分为两大类：一种是依靠“硬件”的方法，即设计精巧的电路直接测量，以过零比较法和电桥平衡为代表。该方法易受到硬件电路的影响而产生干扰，抗干扰能力弱[3]；另一种是采用特定的数学分析方法并最终通过“软件”的方式来实现，以相关分析法[4]、正弦波参数法[5]、谐波分析法[6-7]为代表。谐波分析法采用快速傅里叶变换（FFT）对采集到的电流、电压信号进行谐波分析，提取信号相位角，最终求取介损角。谐波分析法由于能克服谐波、温漂等干扰而得到广泛运用，但在使用中要求整周期采样，否则将会产生频谱泄露和栅栏效应。实际工况下，电网实时频率的波动，导致无法满足正周期采样要求，因而会影响测量精度，需对频谱泄露和栅栏效应进行抑制。其中最有效的抑制方法是对FFT 进行加窗插值。对于加窗插值算法，国内外学者进行了很多相关研究，谢明等学者提出的单峰谱线插值，通过窗函数主瓣内的谱线来求取主瓣中心的坐标，能够得到信号的准确频率和幅值，进而求取相位角，但该方法的测量精度不高，且不适用于处理频率过于密集的信号[8]；卿柏元等推导了Nuttall窗的双谱线插值算法，利用拟合函数求出实用的插值修正公式，降低了误差，但窗函数项数较多时会造成频域函数的复杂化，加大计算的复杂程度和程序的计算量，不利于在线监测的实现[9]；对FFT离散序列重新组合的五点、九点算法，该方法虽然计算精度较高，但需要对离散化的序列进行重新组合[10-11]，翟瑞淼等人提出一种基于Nuttall 窗三峰插值的电力系统谐波检测算法，用曲线拟合得到修正公式，仿真结果表明了该算法相对于单峰及双峰插值精度更高且不需对离散化序列重组[12]。

本文针对离散傅里叶变换存在的能量泄露和栅栏效应，研究了不同窗函数的数谱特性及其插值算法。在此基础上，提出了基于汉宁窗插值算法的容性设备介损角提取方法，并从基波频率波动、采样频率变化、白噪声信噪比变化几个方面对算法有效性进行验证。根据仿真结果，基于汉宁窗插值算法的介损角测量结果相对误差在1%内，且稳定性较好。

1 介损角测量原理

介质损耗指在电场作用下，单位体积的绝缘介质在单位时间内将电能转化为热能的过程中产生的能量损失[13]。电容型设备在交流电压作用下的电介质等效电路可用一个电阻和电容并联或串联来表示，以并联等值电路为例如图1进行测量原理的分析。

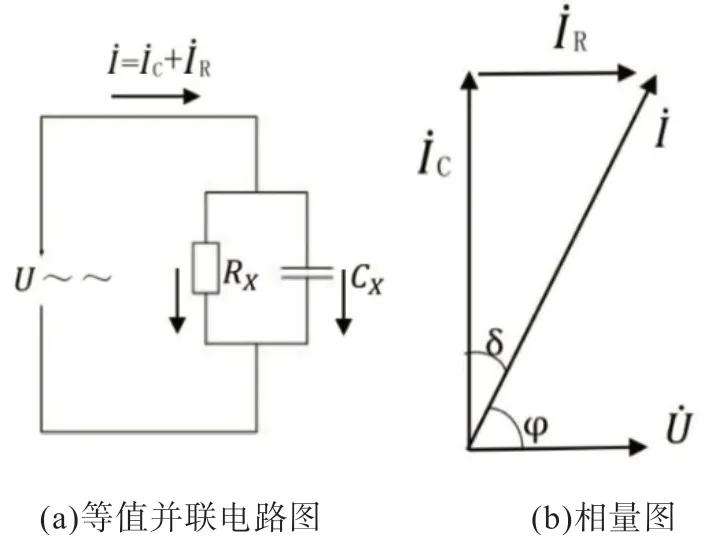
图1电容型设备等值电路及相量图

由式（1）可知：性能较好的绝缘介质，其介质损耗应该很小，其等效电阻RX→∞，阻性电流近似为零，可忽略，电流超前夹角δ为0；反之，当绝缘性能发生劣化时，其绝缘损耗一般会变大，其等效电阻RX减小增大，介损角δ增大。介损角δ与功率因数角φ互余，即：

当外加电压U、角频率ω和绝缘介质相同时，介质损耗功率P和介质损耗角正切tanδ成正比关系。功率损耗为：

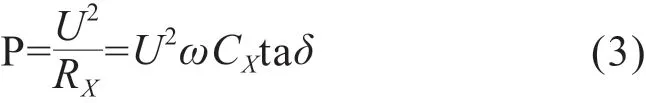
因此，工频下常采用计算介质损耗角正切tanδ来表征电介质的功率损耗。

2 谐波分析法存在的问题

2.1 频谱泄露

信号分析处理时，一般需要对信号进行截断以获取有限长度的离散信号。假设截断信号前的信号为x1(t)=A0sin(ωt+φ0)，经窗函数w(t)截断后为：

该信号的傅里叶变换为：

由式(5)可知，截断信号的频谱图由理论上的ω=±ω0变为了以频点为中心向两边扩展的情况，这种理论频点处的能量分散到附近频点，使得频谱能量不再集中，出现衰减和损失的现象，称为频谱泄露。截断可近似看成加矩形窗，加矩形窗的截断图及矩形窗频谱图如图2 所示。截断后的频谱图出现了泄露，会影响函数频域的特性，最终影响时域参数的求解。

图2矩形窗截断图及其频谱图

2.2 栅栏效应

待处理信号经过DFT 变换后变为等间隔的离散频谱，离散谱线的频率可表示为：

式（6）中：∆f=fs⁄N，k为小于N 的正整数。k是使频率fk最接近f0的谱线。当fk恰好等于f时，得到的时域参数是精准的，而当fk≠f0时，如图3所示，将会产生偏差，只能依据最邻近的离散谱线预估真实频率参量，采用第三根谱线对应的参数进行求解，令f=f3,则实际频率差值为γ=f0-f3，这种现象称为栅栏效应。

当采样为非同步时，fk=(k+σ)∆f,σ∈(-1,1)，频率误差γ=σ∆f，∆f为频率分辨率，∆f越低，误差γ越小。由∆f=fs⁄N 可以推出：增加序列的采样数据量可以有效减轻栅栏效应，而在数据处理的过程中进行频谱校正则是当下抑制栅栏效应的有效途径。

图3栅栏效应示意图

3 基于汉宁窗插值的介损角测量方法

3.1 窗函数的数谱分析

3.1.1 矩形窗离散矩形窗的时域表达式为：

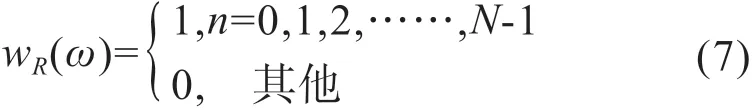
其频谱特性为：

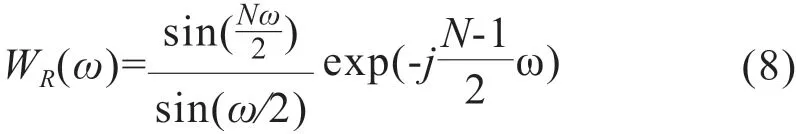
图4矩形窗的时频图

3.1.2 汉宁窗

汉宁窗(Hanning 窗)是广义余弦窗的一种，其表达式为：

其频域表达式可描述为：

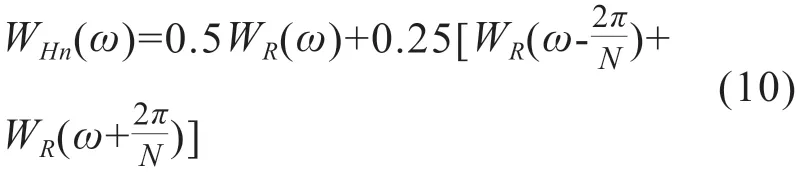
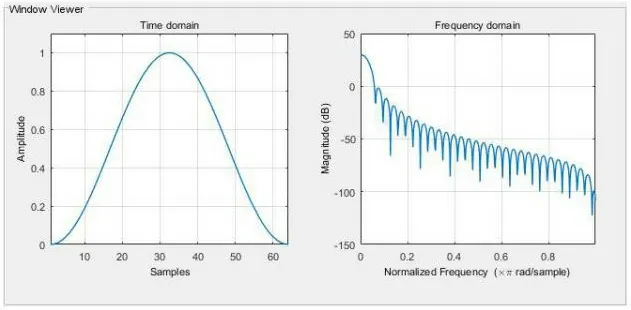
图5汉宁窗的时频图

表1和表2分别给出了矩形窗和汉宁窗的数谱参数和性能对比。

表1两种窗函数数谱参数

从表1中可看出：汉宁窗的旁瓣峰值电平低于矩形窗，旁瓣衰减速率要远大于矩形窗。

表2两种窗函数的性能对比

综合表1、表2 可知：汉宁窗的性能明显优于矩形窗，更适用于提取介损角时频谱泄露的抑制。

3.2 矩形窗和汉宁窗比选

为了比较不同窗函数对于频谱泄露和栅栏效应的抑制效果，分别采用矩形窗和汉宁窗对信号进行校正，并对矫正后的信号进行比较。

若信号采样频率fs选择2000 Hz，f0为模拟信号的频率，φ0为模拟信号的初相位，则模拟信号x1(t)可表示成：

图6为不加窗时的测量结果，以及两种窗函数校正的误差对比。

图6不同方法测量下信号初相位的对比

根据图6，直接对输入信号进行FFT 变换时，实际计算值与原始值相比误差较大，测量得到的初相位随着基波频率的增大而增大，使得最终结果很难用于介质损耗的计算；而窗是一个单位权重的加权函数，加窗的实质是：窗函数与原始时域信号作乘积，相乘之后的信号可更好地满足傅里叶变换的周期性要求，相对误差明显减小，且都小于1%，准确度有了很大的提高。通过横向对比可看出：同频率下，加Hanning 窗的校正效果明显优于矩形窗。矩形窗的结果波动较大，而加汉宁窗的结果则相对稳定，误差小。综上，加Hanning窗对测量结果的精度要明显优于矩形窗，因此本文选用汉宁窗来进行信号相位校正。

3.3 加汉宁窗谐波分析算法

通过二次测量装置获取电压、电流余弦信号，对信号离散化处理后，采用加汉宁窗谐波分析算法，分别得到电压和电流初相位，最后利用公式求解得到介质损耗角。加汉宁窗谐波分析算法计算介质损耗角的流程如图7所示。

图7介质损耗角计算流程图

其中，谐波分析算法流程如图8所示，具体分为4步：

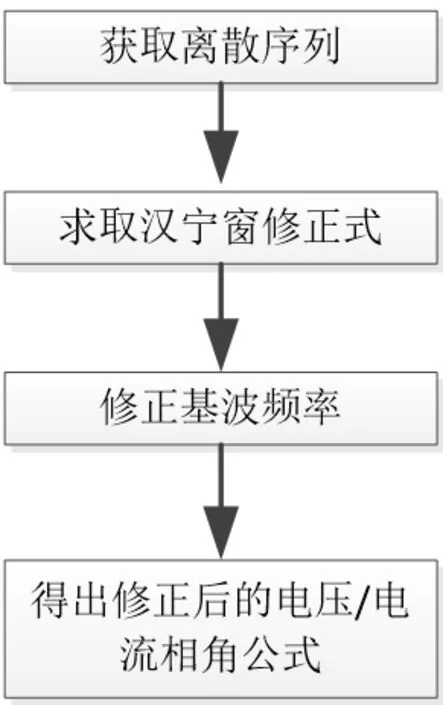
图8谐波分析算法具体步骤

3.3.1 获取离散序列

假设信号Xn是经采样频率fs采样后的离散序列，现利用长度为N 的汉宁窗对其进行加权运算，并做快速傅里叶变换，则结果为：

3.3.2 求取汉宁窗修正式

由汉宁窗谱图可知：幅值谱谱峰主瓣内的两条谱线YK、YK+1经过平移后可以得到对应的重心坐标x0为（k代表第k根谱线）：

同理可得谱线YK-1、YK平移后的重心坐标为：

由此可得汉宁窗的修正式为：

3.3.3 修正基波频率

若信号的采样持续时间为∆t，采样频率为fs，f0为信号的基波频率，理想状况下的电网工频为50.0 Hz，N1为一个周期对应的采样点数，总采样点数为N，k 代表第k 根谱线，则频率分辨率∆f可表示为：

对于非同步采样，由于存在误差，需要进行校正，这里添加一个修正值∆k，修正后的基波频率为：

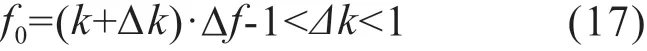
3.3.4 修正后的电压电流相角公式

由汉宁窗的相位因子可得修正后的相角：

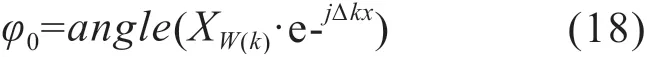
若实际监测系统测得的电压、电流信号初相位为φu0和φi0,则介质损耗角δ为：

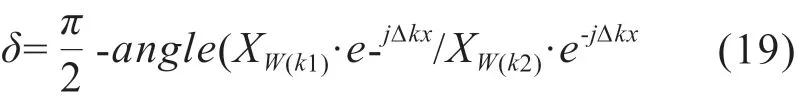
4 仿真分析

假设含谐波的电流、电压信号表达式为：

式(20)中,UM、IM分别为m 次谐波的电压和电流幅值，fm为m 次谐波频率，m=1时为信号的基波频率。

本次仿真通过改变基波频率f1来验证算法抵抗频率波动能力；改变原有的采样频率fs来观察测量结果的变化；最后分别为电流、电压信号添加了信噪比不同的白噪声，研究该算法对噪声的适应能力。

1）基波频率f0波动时的仿真

取采样频率为1500 Hz，采样点数N 为1024个。由于流过被测介质的电流基本为电流超前电压的功率因数角φ≈90°，且略小于90°，选取电压相位的初相位φm=60°，电流相位的初相位为φn=149.73°，通过理论即可计算得出其介质损耗角δ=0.004712388。

电网实际频率具有时变特性，频率偏差的大小会受到系统容量的影响，考虑电网工频波动最大的情况，即对f0取49.5～50.5 Hz进行分析，仿真部分数据如表4所示。图9给出了基波频率变化时，介损角测量相对误差的变化曲线。

表3频率波动对仿真结果的影响

图9基波频率变化时，介损角的相对误差变化

从表3中可看出：对电流、电压离散系列加Hanning窗插值的介损角测量的相位误差均低于1%，受基波频率波动影响的范围较小，满足测量要求。由图9可看出，基波频率变化时，其与电网工频的差距越小，采用加Hanning 窗插值的介损角测量误差也越小。

2）采样频率fs变化时的仿真分析

现假设信号的基波频率不变，为50.5，根据香农定理可知保持频率不失真的最低采样频率为100.4 Hz。仿真实验取采样频率fs分别取300 Hz、600 Hz、1000 Hz、1200 Hz、1500 Hz和2000 Hz 对介质损耗角进行计算，仿真结果如表4所示。

表4采样频率变化对仿真结果的影响

从表4可看出：在一定范围内，采样频率增加会使得计算值的相对误差会渐渐降低，在1000 Hz 左右时，误差最小，最优采样频率可能在1000 Hz 左右，但不能仅追求采样频率的提高而忽视了硬件系统与频率的协调性，超过了一定值后，提高频率反而会造成测量精度的下降，因此需要合理设置采样频率。

3）随机白噪声变化时的仿真分析

设置模拟信号频率为49.6 Hz，利用Matlab中的函数加入白噪声，控制SNR（信噪比）的值分别为：5、15、20、40、70、90、110 dB，并多次求值计算介质损耗角的平均值，以此减轻白噪声随机性的影响，白噪声SNR 变化对测量结果的影响如表5所示。图10为白噪声信噪比和介损角测量相对误差两者的变化曲线。

由表5和图10可以看出，仿真结果和分析结果基本一致，即添加的随机白噪声信噪比越小，测量值的相对误差就越大。当信噪比低于20 dB时，对测量结果的精度影响很大，但当信噪比大于等于40 dB时，误差回到了测量结果的合理区间，表明此时窗插值算法可以满足测量精度的要求。

表5白噪声SNR变化对仿真结果的影响

图10白噪声变化时，介损角测量的相对误差变化

5 结束语

本文提出了基于Hanning 窗插值算法的容性设备介损角测量算法原理和流程图，通过仿真从基波频率波动、采样频率变化、白噪声信噪比变化三方面对算法进行了验证。根据仿真结果，本算法介损角测量相对误差在1%内，且测量相对误差曲线波动小，稳定性较好。

通过仿真分析得到以下结论：

1）当系统频率发生波动时，基于Hanning窗插值算法的容性设备介损角测量结果准确性满足要求；

2）采样频率需要满足奈奎斯特-香农采样定理才能有效避免严重误差的出现，当采样频率增加到一定值时，频谱增大带来的测量误差降低不再明显。过高的采样频率会增加硬件的投资和维修保养费用，实际工程中采样频率需要合理适度设置；

3）本文算法对含有较高信噪比的信号处理时具有较好的适应性，但当信噪比较低时误差很大，实际运用中有必要加装消噪装置。