基于p-q变换的改进ip-iq基波正序有功和无功电流检测算法

胡志坤，胡锰洋，桂卫华，阳春华，何志敏

(1. 中南大学 物理科学与技术学院，湖南 长沙，410083；2. 中南大学 信息科学与工程学院，湖南 长沙，410083)

电力电子非线性设备产生大量谐波和无功电流注入电网，这些负荷的非线性、冲击性及不平衡的用电特性使电力系统电压电流波形发生畸变，甚至引起电压波动、闪变和三相不平衡，严重影响供电质量。采用有源电力滤波器、STACOM等电力电子设备进行谐波治理和无功补偿成为治理电网谐波、补偿无功的一类最重要装置[1-5]。无功补偿包含对基波无功功率的补偿和对谐波无功功率的补偿，因此，在非理想电压下对基波无功电流进行检测，对实现包括基波无功补偿在内的综合电力补偿有重要意义。基于瞬时无功理论[6-7]的p-q算法仅能在三相电压正弦且对称时准确检测基波无功电流[8]，ip-iq算法在电网电压存在畸变时仍然能够准确地检测负载电流中的基波正序分量，但在三相电压不对称和存在畸变情况下均无法得到基波正序电流的有功和无功分量[9-10]。张桂斌等[11-12]只考虑了谐波和基波负序电流的检测；谢运祥等[13-14]提出了准确检测基波正序有功电流的方法，但先后2次使用低通滤波器，计算复杂，系统延时较大。本文对畸变不对称的三相电压、电流同时进行p-q坐标变换和低通滤波，以在p-q坐标系下电流矢量向电压矢量及其法线方向投影的方式，获取了基波正序有功和无功电流，并有效降低低通滤波器延时，为电力系统中实现对谐波、基波负序电流和基波正序无功电流的综合补偿提供了合理的指令参考电流。

1 基于瞬时无功理论的ip-iq算法分析

本文以三相三线制电网为例进行分析。由于三相三线制电网中负载谐波电流不存在零序分量而三相电网电压可以存在零序分量[15]，按照对称分量法，可分别将其表示为：

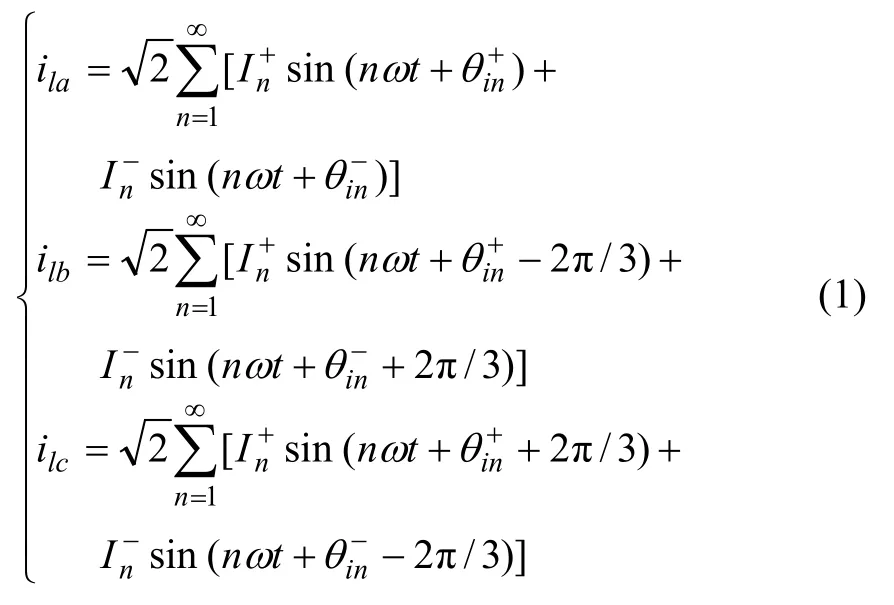
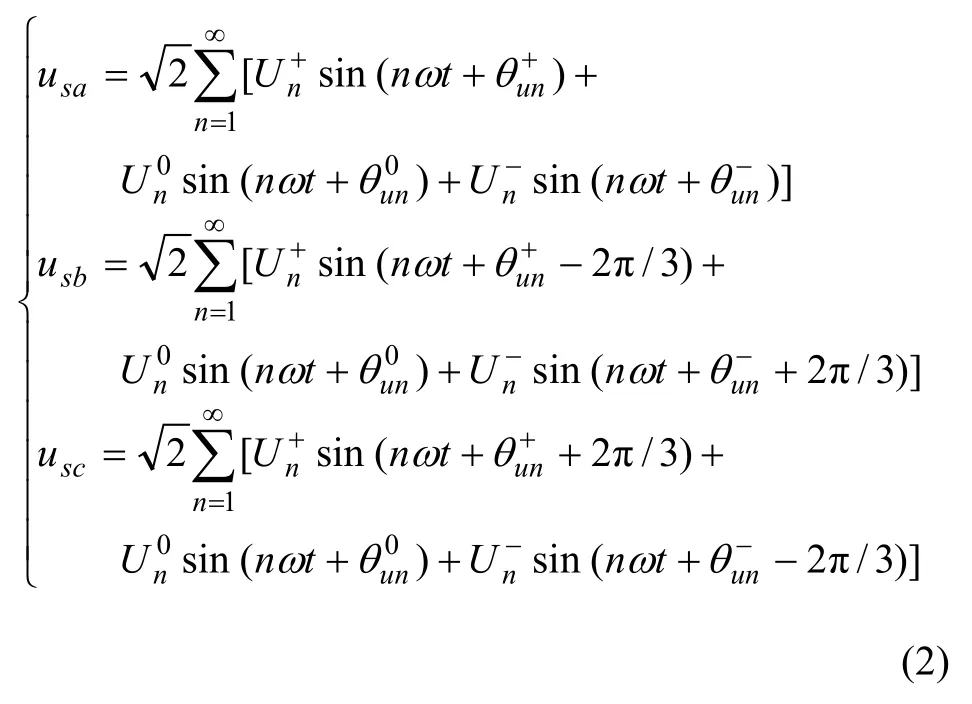
式中：ila，ilb和ilc为三相负载谐波电流；usa，usb和usc为三相电网电压；I和U分别为电流、电压有效值；ω为角频率；θ为初相角；下标u和i分别表示电压和电流；下标n为谐波次数；上标“+，-和0”分别代表正序、负序和零序，如表示n次谐波电流正序分量的相角。

使用ip-iq算法检测基波正序电流的原理如图1所示。其中：iaf，ibf和icf为基波正序电流；为指令电流，包含各次谐波和基波负序电流；PLL(Phase lock-loop)为锁相环电路，它与信号发生器一起可以获得与A相电网电压频率和相位相同的正、余弦信号。图 1中矩阵C2/3为三相电压(或电流)转换到α-β坐标系的转换矩阵，C3/2矩阵为从α-β坐标系到三相坐标系的转换矩阵，分别表示如下：

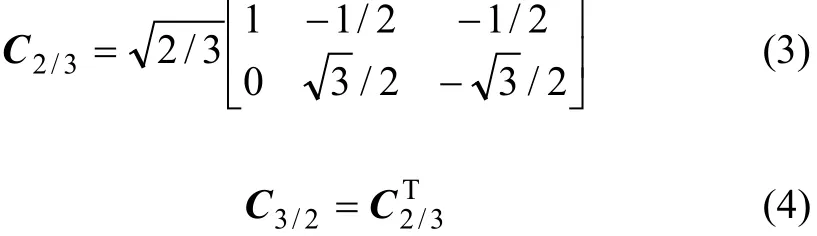
设通过 PLL检测到的A相电网电压相位为ωt+γ(γ∈ [0, 2π])，γ表示式(2)中存在畸变和不对称分量的A相电压初相角。

图1 ip-iq检测算法原理框图Fig.1 Priciple diagram of ip-iq detecting method

根据A相电压相位构造正、余弦转换矩阵如下：

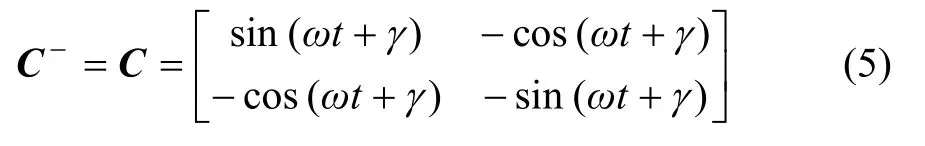
对图1中得到ip和iq[13]经过低通滤波器(LPF)处理，得出直流分量为：

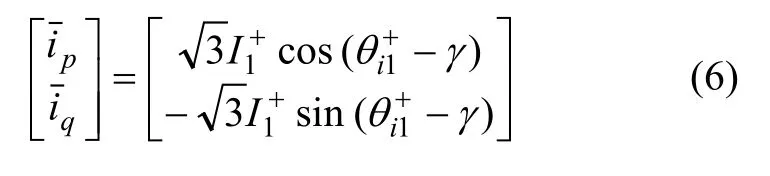
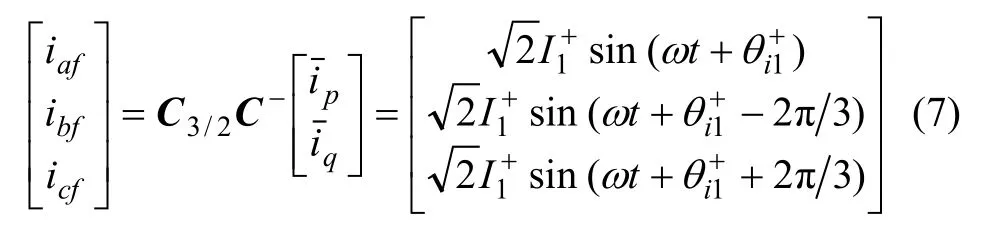
但是，该算法采用切断ip或iq通道的方法不能准确求取基波正序无功或有功电流。例如，采用切断图1中iq通道的方法求取基波正序电流的有功分量，结果分别用表示，则式(7)将变为：

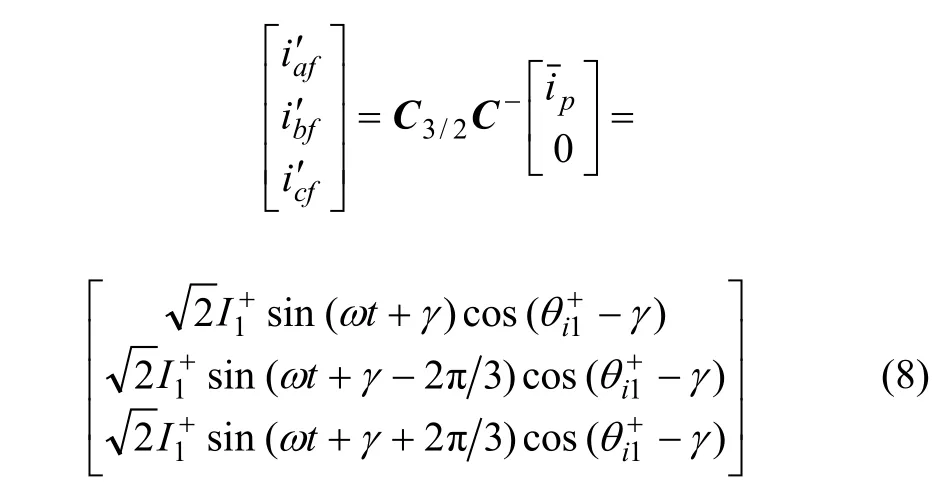
2 基于p-q变换的改进算法

为获得准确的三相基波正序有功电流，对三相电网电压在ip-iq算法中也进行类似三相电流变换以获取基波正序电压的相位信息，并行地对所得出转换结果同时进行低通滤波，以降低低通滤波器总延时，然后，在引出的p-q坐标系下将滤波后的电流矢量向电压矢量及其法线方向上投影，经过反变换获取基波正序电流的有功分量，如图2所示。

设三相负载电流和电网电压分别如式(1)和式(2)所示，通过 PLL检测到的A相电网电压相位仍设为图2中的算法中的结果相同，如式(6)所示。根据图2所示步骤，可得为：

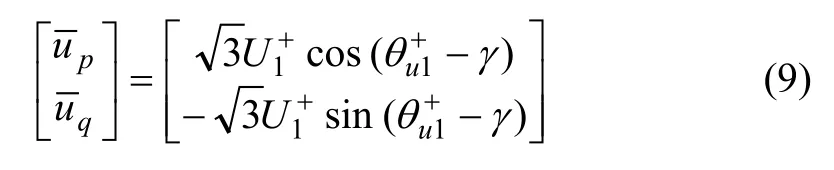
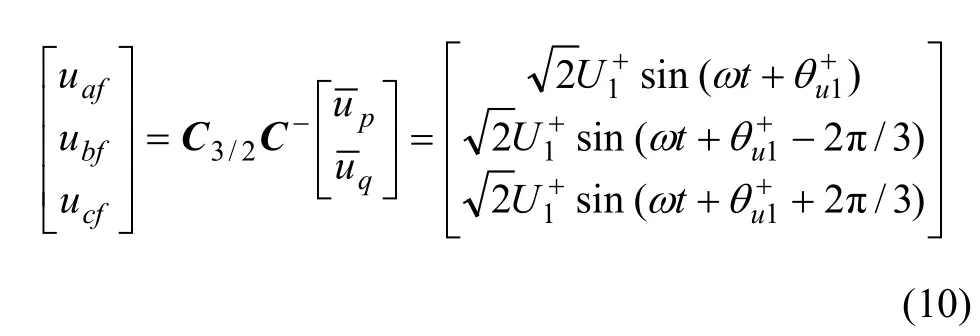
这里引入正交的p-q坐标系，如图3所示。图3中：式(6)的计算结果分别作为p-q坐标系中矢量i的p和q坐标；式(9)的计算结果分别作为p-q坐标系中矢量u的p和q坐标。

定义1在p-q坐标系下，电流合成矢量i在电压合成矢量u上的投影iu为瞬时正序有功电流矢量，电流合成矢量i在电压合成矢量u法线方向上的投影为瞬时正序无功电流矢量。三相电流(电压)变换到p-q坐标系的公式为：

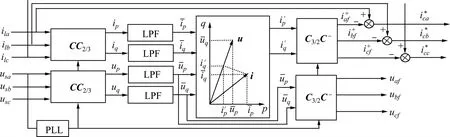
图2 改进的ip-iq算法原理框图Fig.2 Principle diagram of improved ip-iq detecting method

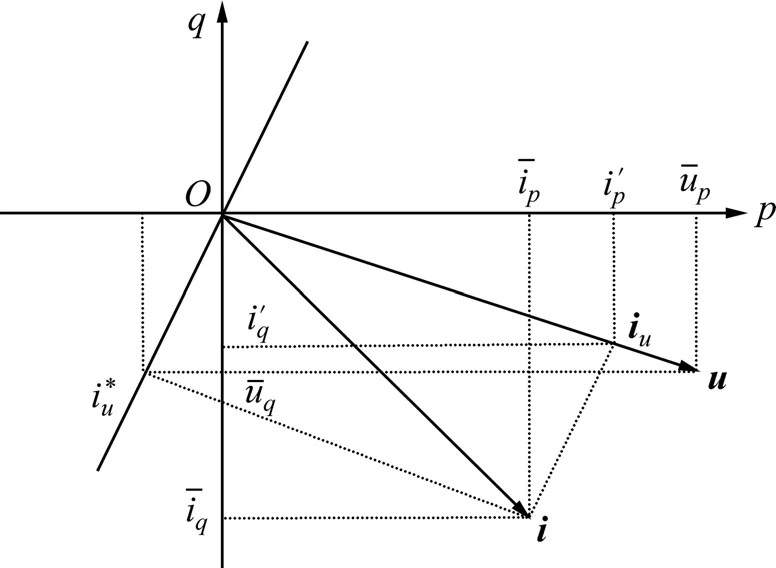
图3 p-q坐标系下电压和电流矢量图Fig.3 Vector diagram of voltage and current in p-q coordinate system

3 仿真验证

针对电网电压对称且无畸变、电网电压不对称、电网电压同时存在畸变和不对称3种情况，在Matlab环境下对ip-iq算法和本文改进算法的检测结果进行仿真。非线性负载选用三相桥式晶闸管整流电路，电感Lt=1 mH，电阻Rt=1.5 Ω，导通角为0°。电压源对称无畸变时相电压有效值为220 V，A相电压初相角为0°。

3.1 电网电压对称且无畸变

图 4所示为理想电网电压条件下的三相负载电流，含有大量的谐波和无功电流分量。使用本文的改进算法获取的A相基波正序电压和A相基波正序有功电流如图5所示。

图4 电网电压对称且无畸变条件下的三相负载电流Fig.4 Three-phase load current waves under ideal voltage supply conditions

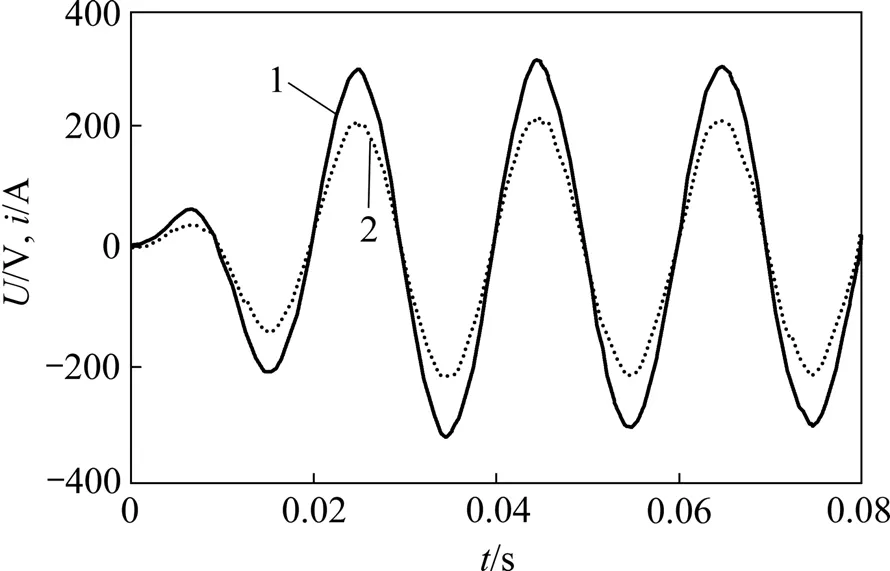
图5 A相基波正序电压与A相基波正序有功电流Fig.5 Positive fundamental voltage and active current of phase A

由于电网电压对称且不存在畸变，图5中的A相基波正序电压与A相电网电压相同。从图5可以看出：所提取的电流与A相基波正序电压有相同的相位，证明采用该算法在理想电压情况下能够正确获得基波正序有功电流。

图6所示为基波正序电压与ip-iq算法中断开iq支路前后提取的基波正序电流比较结果，其中：图 6(a)所示为断开iq支路前的比较图，A相基波正序电流与A相基波正序电压存在相位差，说明基波正序电流中含有无功分量；图6(b)所示为断开iq支路后的比较图。图6中的A相基波正序电流与A相基波正序电压具有相同的相位，为基波正序有功电流。因此，在电网电压对称且不存在畸变时，通过断开iq支路的方法，ip-iq算法也能获得准确的基波正序有功电流。

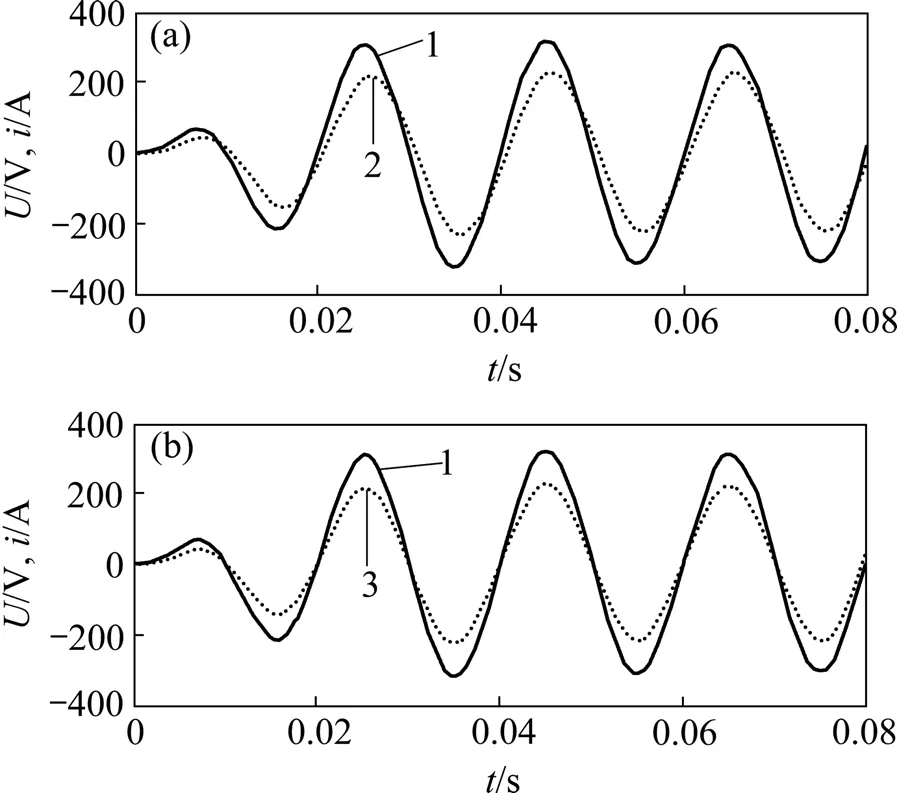
图6 A相基波正序电压与ip-iq算法断开iq支路前后提取的A相基波正序电流Fig.6 Phase A positive fundamental voltage and positive fundamental current obtained by ip-iq method before and after iq branch is broken

3.2 电网电压不对称

图7所示为三相电网电压不对称，且A，B和C三相电压初相位分别为25°，-125°和120°时，改进算法得到的基波正序电压与传统ip-iq算法中切断iq支路后得到的电流比较结果。

从图7可见：电流波形与电压波形有较大的相位差，所提取电流不是基波正序有功电流。其原因是ip-iq算法不能获得三相基波正序电压准确的相位信息。

图8所示为电网电压不对称时，改进算法检测到的三相基波正序电压与基波正序有功电流。

从图8可见：在电网电压不对称时，该算法所检测到的基波正序有功电流与基波正序电压有相同的过零点，因此，二者具有相同的相位，证明该算法在电网电压不对称时可以获得正确的基波正序有功电流。

3.3 三相电网电压存在幅值畸变且不对称

参考 GB/T 14549—1993《电能质量公用电网谐波》的标准，假设A，B和C三相电压初相位仍然分别为25°，-125°和120°，在此基础上分别在三相电压上增加10%的5次谐波和5%的7次电压谐波。

由于ip-iq算法不受电压畸变因素的影响，在畸变不对称电压条件下采用切断iq支路的方法获得的基波正序电流与图7所示的相同。因此，在该条件下采用传统ip-iq算法仍不能准确提取基波正序有功电流。研究结果表明：采用改进算法所提取的基波正序有功电流与三相基波正序电压具有相同的相位，证明在电网电压同时存在相位不对称和幅值畸变的复杂电压条件下，采用改进算法仍然能够正确检测出基波正序有功电流。

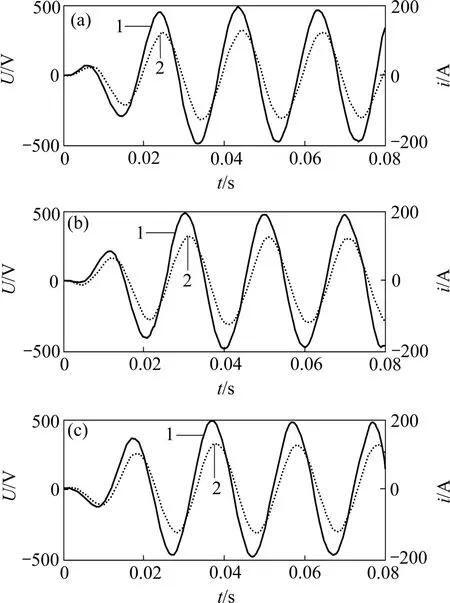
图7 三相基波正序电压与ip-iq算法断开iq支路后提取的基波正序电流Fig.7 Positive fundamental voltages and currents obtained by ip-iq method after iq branch broken

4 结论

(1)基于在p-q坐标系下对瞬时正序有功电流和瞬时正序无功电流的定义，准确地获得了基波正序有功和无功电流。在电网电压存在畸变和不对称条件下进行的仿真试验证明了本文所提出算法在各种非理想电源电压情况下的适用性，为在复杂电压条件下实现包含谐波和基波无功的综合补偿提供了合理的参考指令电流。

(2)在三相三线制电网中，利用本文所提出算法得到的基波或任意次谐波的正、负序有功(无功)电流，可以得到基波或任意次谐波的有功(无功)电流，因此，为对任意次谐波电流或其有功(无功)电流分量进行单独补偿提供了依据。

(3)A相电压的初相角γ可为[0，2π]区间内任意值，且并不反映到所检测到的基波正序(有功和无功)电流中，可知锁相环(PLL)的作用在于检测电网电压的角频率而非瞬时相位，ip-iq算法和改进算法均不要求所生成的正、余弦矩阵C和C-与A相电压相位同步，因此，在电网电压频率畸变可以忽略时，可以预先设定电压角频率，从而省略锁相环电路。

[1] Aredes M, Heumann K. A universal active power line conditioner[J]. IEEE Trans on Power Delivery, 1998, 13(2):545-551.

[2] 陈国柱, 吕征宇, 钱照明. 有源电力滤波器的一般原理及应用[J]. 中国电机工程学报, 2000, 20(9): 17-21.CHEN Guo-zhu, LÜ Zheng-yu, QIAN Zhao-ming. The general principle of active power filter and its application[J].Proceedings of the CSEE, 2000, 20(9): 17-21.

[3] 赵巍, 涂春鸣, 罗安, 等. 针对大功率非线性负载的有源滤波器[J]. 中南工业大学学报: 自然科学版, 2002, 33(2): 201-204.ZHAO Wei, TU Chun-ming, LUO An, et al. Active filter for high-power nonlinear loads[J]. Journal of Central South University of Technology: Natural Science, 2002, 33(2):201-204.

[4] 李承, 邹云屏. 有源电力滤波器抑制谐波的机理分析[J]. 电力系统自动化, 2003, 27(20): 31-34.LI Cheng, ZOU Yun-ping. Active power filter to suppress harmonic caused by nonlinear load[J]. Automation of Electric Power Systems, 2003, 27(20): 31-34.

[5] 罗德凌, 周方圆, 唐朝晖. 有源电力滤波器的研究现状与发展动向[J]. 国外电子测量技术, 2006, 25(2): 1-4.LUO De-ling, ZHOU Fang-yuan, TANG Chao-hui. Active power filters and their new development tendency[J]. Foreign Electronic Measurement Technology, 2006, 25(2): 1-4.

[6] Akagi H, Kanazawa Y, Nabae A. Generalized theory of the instantaneous reactive power in three-phase circuits[C]//Proceedings of JIEE IPEC. Tokyo, 1983: 1375-1386.

[7] Akagi H, Kanazawa Y, Nabae A. Instantaneous reactive power compensators comprising switching devices without energy storage compensators[J]. IEEE Transactions on Industry Applications, 1984, 20(3): 625-630.

[8] EI-Habrouk M, Darwish M K, Mehta P. Active power filter: A review[J]. IEE Proc Electr Power Appl, 2000, 147(5): 403-413.

[9] 马大铭, 朱东起, 高景德. 三相电压不对称时谐波和无功电流的准确检测[J]. 清华大学学报: 自然科学版, 1997, 37(4):7-10.MA Da-ming, ZHU Dong-qi, GAO Jing-de. Accurate detection for harmonics and reactive currents in the case of unsymmetrical three phase voltages[J]. Journal of Tsinghua University: Science and Technology, 1997, 37(4): 7-10.

[10] 杨君, 王兆安. 三相电路谐波电流两种检测方法的对比研究[J]. 电工技术学报, 1995(2): 43-48.YANG Jun, WANG Zhao-an. A study on the comparison of two methods used to detect the harmonic currents of three-phase circuits[J]. Transactions of China Electrotechnical Society,1995(2): 43-48.

[11] 张桂斌, 徐政, 王广柱. 基于空间矢量的基波正序、负序分量及谐波分量的实时检测方法[J]. 中国电机工程学报, 2001,21(10): 1-5.ZHANG Gui-bin, XU Zheng, WANG Guang-zhu. Study and simulation of real-time detecting method for fundamental positive sequence, negative sequence components and harmonic components based on space vector[J]. Proceedings of the CSEE,2001, 21(10): 1-5.

[12] 陈海荣, 徐政, 钱向明. 空间矢量法自适应检测基波正负序及谐波分量[J]. 高电压技术, 2006, 32(10): 85-90.CHEN Hai-rong, XU Zheng, QIAN Xiang-ming. Adaptive detecting method for fundamental positive sequence, negative sequence components and harmonic components based on space vector[J]. High Voltage Engineering, 2006, 32(10): 85-90.

[13] 谢运祥, 陈坤鹏, 邓衍平, 等. 改进型谐波与基波有功和无功电流检测法[J]. 华南理工大学学报, 2005, 33(4): 15-19.XIE Yun-xiang, CHEN Kun-peng, DENG Yan-ping, et al.Improved detecting method for harmonic and fundamental active and reactive currents[J]. Journal of South China University of Technology, 2005, 33(4): 15-19.

[14] 王玉斌, 吕燕, 李英俊. 三相电压不对陈时谐波和无功电流的准确检测新方法[J]. 继电器, 2006, 34(18): 47-51.WANG Yu-bin, LÜ Yan, LI Ying-jun. New precision detection method of harmonics and reactive current under asymmetrical three-phase voltages[J]. Relay, 2006, 34(18): 47-51.

[15] 王兆安, 杨军, 刘进军. 谐波抑制和无功功率补偿[M]. 北京:中国机械工业出版社, 1998: 30-70.WANG Zhao-an, YANG Jun, LIU Jin-jun. Harmonic control and reactive power compensation[M]. Beijing: China Machine Press,1998: 30-70.