基于样本加权矩阵的自适应弱目标识别鲁棒算法

陈炳权 ，刘宏立

(1. 湖南大学 电气与信息工程学院，湖南 长沙，410082；2. 吉首大学 物理科学与信息工程学院，湖南 吉首，416000)

弱目标识别是目前模式识别和人工智能领域的研究热点，研究者们提出了很多用于诸如人脸等弱目标识别的方法[1-5]。自从 Turk等[6]利用重构权向量作为识别特征提出“特征脸”识别技术以来，人脸识别领域迎来了“基于表征”的子空间分析方法研究热潮，其中代表性方法有主成分分析法(PCA)[6]、线性判别分析法(LDA)[7-9]、独立成分分析法(ICA)[10]以及Bayesian方法[11]、基于核技术的 Kerne1 PCA[12]和 Kerne1 LDA[13]等。以上算法都有1个共同的特点：在提取特征时，只重视整个人脸的总体特征，而忽略了眼睛、鼻子等作为人脸局部的存在。事实上，如果不考虑整个人脸，人脸关键部位的局部特征也有其自身的鉴别能力，它们对人脸识别也是很有帮助的。当然，人脸的各个部位其鉴别重要性程度是不同的，因此，它们在人脸识别中所起的作用也不同。一些研究人员对此进行了研究，如：Martinez等[14]用统计的方法比较了正面人脸不同的 48个特征点在描述整个人脸模式中所起的作用，并据此赋予它们不同的权值；Pentland等[15]则将“特征脸”技术用于识别人脸各局部器官，从而产生“特征眼”、“特征鼻”、“特征嘴”等概念，融合各“特征器官”以达到人脸识别的目的；Wang等[16]提出的算法也对人脸面部局部特征“个性化程度”问题进行了研究。在此，本文作者在已有的理论基础上提出一种多区域特征加权融合思想，并将其应用于传统的PCA-LDA算法之中，用样本加权特征矩阵代替传统的特征向量得到1种新的投影准则，即加权自适应PCA-LDA算法。

1 全局特征提取

小波变换具有很好的时空域局部化特性，对一维或二维信号具有很强的特征提取能力。小波包分解通常将图像分解为低频平滑部分、水平细节、垂直细节和对角线细节4部分，常被应用于信号处理中；因此，在全局特征提取中，选用小波分解来提取信号主要特征。如果对训练集人脸进行二维小波变换，分解成以上4部分，那么，可以组成4个样本空间，然后，用主成分分析法(PCA)分别提取出这4个部分的β1，β2，β3和β4个最大的特征值对应的“特征脸”，分别组成4个规范正交的变换阵P。将每个样本用P进行变换，得到每个样本在每个小波子空间上的特征向量，分别为：将这4个向量合并为向量Xq，即

其中：β=β1+β2+β3+β4；样本的全局特征向量Xq包含了人脸在4个小波子空间的主要特征。由式(1)可知：全局特征向量Xq维数较高。

2 关键局部特征提取

通常局部特征指的是正面人脸中眉、眼、鼻、嘴共4个子区域，它们包含了人脸面部的主要信息。局部区域的切割依赖于人脸特征点的准确定位。本文重点研究识别算法。假定一些关键特征点(如眉角、眼角、鼻侧点、嘴角)已通过前端的检测模块准确定位，通过适当的归一化处理可以得到4个训练样本集。

采用基于Gabor小波变换的方法来提取以上分解的4个关键局部特征。与通常Gabor小波变换提取特征的方法不同，这种方法对每个关键局部提取的特征维数较少，这样，一方面，能有效地减少计算量；另一方面，虽然局部特征非常重要，但是，对于每个局部特征，它在辨识过程中的相对重要性比起全局特征来说要低很多，因此，维数不必过大。使用更加简便的方法，使得特征向量的维数进一步降低。设 2维Gabor滤波器有如下形式：

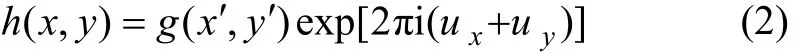
其中：

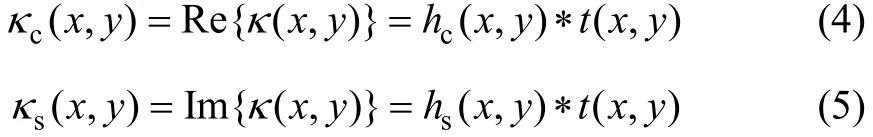
κ(x,y)的振幅m(x,y)和相位ψ(x,y)分别为：

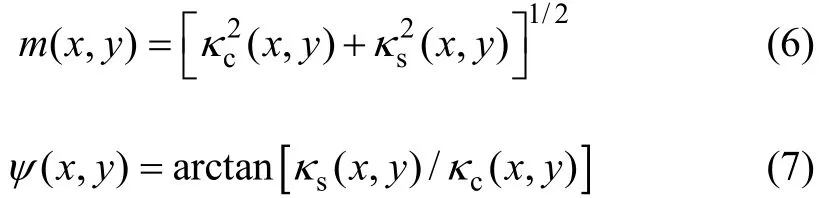
上述应用的展开式为

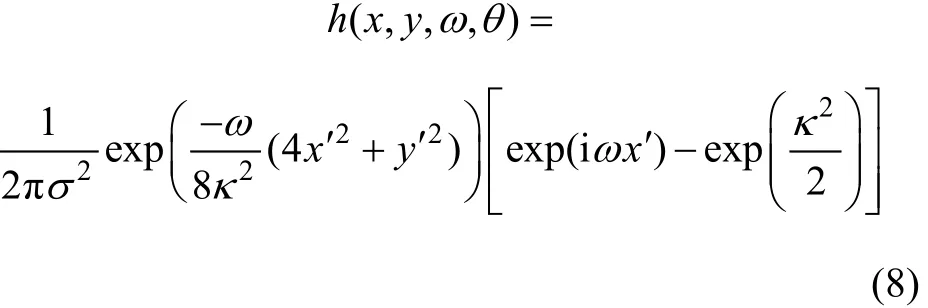
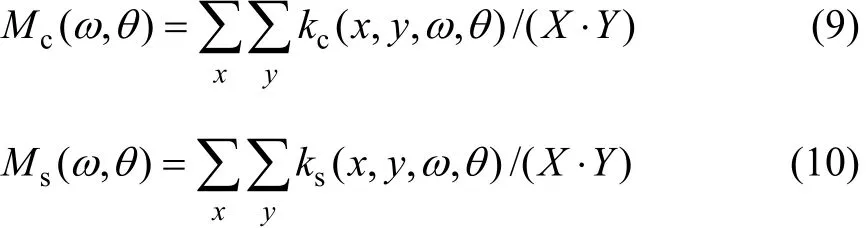
滤波器响应的实部和虚部的标准差分别为：

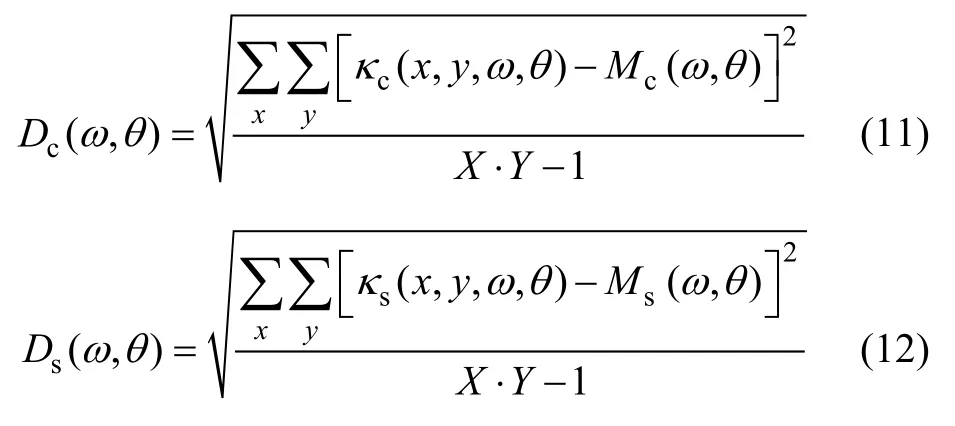
这里直接选取每个样本的Gabor统计量作为样本的特征表示，通常有2个不同的ω和4个不同的θ，则其局部特征向量可以表示为：

通过Gabor小波提取分割后的4个人脸关键局部特征，可得4个特征向量，分别为V1，V2，V3和V4，每个特征向量为2×4×4即32维。

3 多区域特征融合的加权 PCA-LDA算法

3.1 多区域特征权值的选择

将人脸的全局和4个关键的局部特征提取出来，就可以根据相应的算法进行特征融合。其步骤是：首先将全局和4个关键局部特征向量简单地叠加，组成1个向量，再用相应的算法进行人脸识别；对全局和2个关键局部特征分别用算法进行识别，然后，用模糊数学中的相应方法将识别结果进行综合，得出最终类。该方法的缺陷是：虽然局部特征在人脸识别中非常重要，但是，对于每个局部特征，它在辨识过程中的相对重要性与全局特征相比要低很多；另一方面，即使在4个关键局部特征之间，它们在人脸识别中的重要性也有差异[16]。所以，简单地将全局和4个关键局部特征向量叠加，很难反映出全局和局部特征在人脸识别中的重要性。因此，本文引入人脸识别中的全局和局部特征重要性权值。识别率较高的特征，其特征向量的权值较大；相反，识别率较低的特征，其权值较低。由于全局是由局部组成，在人脸识别中的重要性最大的权值最高，而局部特征的权值较低。权值选择的方法很多，可以根据经验，也可以通过实验来测得。笔者在文献[4]的基础上设计了一种基于PCA-LDA的方法来得到权值，其具体设计方法如下。

(1)设人脸训练集中类的个数为C，每类人脸的个数为N，d维列向量表示第i类中第m个样本，故训练集中共有M=N×C个样本。

(2)由这些差值构成 1个协方差矩阵，求出这个矩阵的前β阶最大特征值的特征向量，然后，把这些向量组合起来构成1个PCA投影矩阵，设为WPCA。

(3)用该PCA投影矩阵把所有的训练样本投影到1个β维子空间中。

(4)将得出的最佳描述特征分别构成类内散布矩阵Sw和类间散布矩阵Sb，计算矩阵的前t个最大特征值的特征向量，由这些向量构成1个LDA投影矩阵，设为WLDA。

其中：i=1, 2, …,C；m=1, 2, …,N；n=1, 2, 3, 4。

(6)求出 4个关键局部所有样本类内距离的平均值LW(n)，即

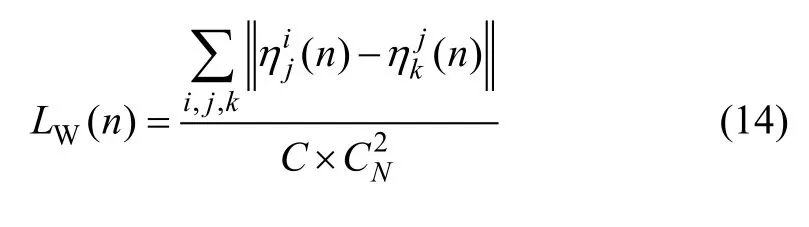
其中：1≤k＜j≤N;n=1, 2, 3, 4。

(7)求出 4个关键局部所有样本的类间距离的平均值LB(n)：

该法借鉴了文献[4]中普通的人脸识别 PCA-LDA算法，得出了全局样本的最佳投影方向，并分别将关键局部样本投影到此方向，计算出样本的类间距离平均值与类内距离平均值的比值，以此来决定不同局部的权值。从式(16)可见：比值L(n)越大，说明其可识别性越大，所以，其重要性权值就越大。

3.2 多区域特征加权融合原理

定理11个形如式(17)的矩阵，其特征值分别为其对角线上子矩阵特征值的集合。

定理21个形如式(17)的矩阵，X，K(1),K(2),K(3)和K(4)为矩阵A的子矩阵，X为n维方阵，K(1),K(2),K(3)和K(4)分别为m1,m2,m3和m4维方阵，设m1+m2+m3+m4=p，若ξ是X的特征向量，则为A的特征向量；若ξ是K(1)的特征向量，则A的特征向量，依此类推。

由定理1可知：矩阵A的特征值为全局样本和局部样本协方差矩阵X，K(1),K(2),K(3)和K(4)的特征值的集合，求出这个矩阵的前β个最大特征值的特征向量，然后，把这些向量再组合起来构成1个投影矩阵，即加权PCA投影矩阵，设为Wwpca。如果已知式(1)子矩阵的特征值和特征向量，就得到矩阵A的特征值和特征向量；特征值不变，而特征向量则在子矩阵的特征向量上前后补0，增加到与矩阵A相同的维数即可。

对全局样本和关键局部样本加权后，分别根据标准 PCA方法求得它们与均值之差的协方差矩阵，然后，对角组合成矩阵A，取其β个最大特征值的特征向量，把这些向量组合起来构成1个投影矩阵Wwpca，这样，样本就可以根据这个投影矩阵进行投影。但是，样本特征不能是全局和加权局部样本简单的拼接，因为这不符合上述矩阵A的对角组成原理，也不符合基本PCA的原理。为了解决这个问题，引入样本加权的特征矩阵即

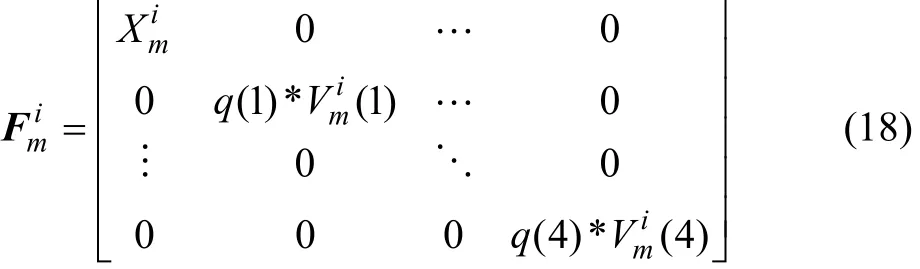
对于样本更复杂的特征矩阵，提出类矩阵(Class matrix)概念，该矩阵只与类有关，与每类的样本无关，由每类样本可以得出1个类特征矩阵。这样，在进行人脸识别过程中，可以大大减少计算复杂度。设是 1个标准正交向量，则类矩阵为

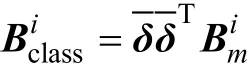
基于类矩阵的人脸识别解决了 LDA的小样本空间问题，且识别速度较快。

3.3 加权PCA-LDA人脸识别算法

笔者在文献[1]基础上设计了 1种新的加权PCA-LDA人脸识别算法，其步骤如下：(1)先分别求出全局样本向量和 4个关键局部样本向量以及对应的样本向量平均值的差值；然后，求出它们的协方差矩阵X和K(n)(n=1, 2, 3, 4)，再据式(17)得出矩阵A。

(2)求出矩阵A的前β个最大特征值的特征向量，然后，把这些向量组合起来构成1个PCA投影矩阵WWPCA。其中：WWPCA是1个(n+m1+m2+m3+m4)×β阶的矩阵。

(3)根据式(18)得出所有训练样本和实验样本的特征矩阵

(4)用PCA投影矩阵把所有的训练样本投影到1个K维子空间，即是1个β×5阶的矩阵。

(5)把上面得出的最佳描述特征分别构成类内散布矩阵SW和类间散布矩阵SB。虽然训练样本由特征向量变成了β×5阶的特征矩阵，但是，其类内散布矩阵与类间散步矩阵的求法是一样的，即

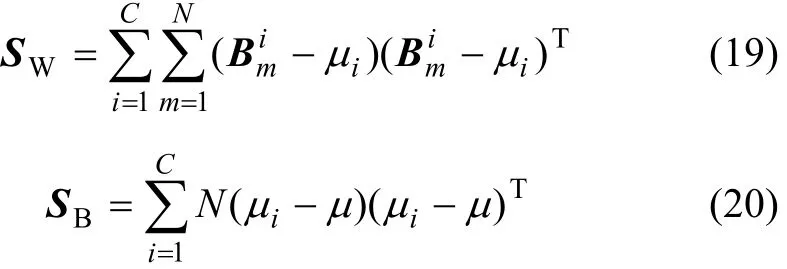
其中：μ为所有样本的均值；iμ为第i样本的均值。计算矩阵前t个最大特征值的特征向量，由这些向量构成1个LDA投影矩阵WWLDA。

(6)使用WWLDA把式(4)得出的矩阵B投影到1个t维子空间，得出最佳分类特征矩阵即，并根据这些特征组成1个C类特征人脸识别数据库。

(7)把实验人脸图像减去平均脸求出差值矩阵S，把S进行 2次投影变换，得出最佳分类特征：

(8)计算实验人脸和人脸识别数据库中每 1类样本距离的平均值，平均距离最小的类即为实验人脸所属的类。

4 实验验证

采用的CBR人脸库由100个人组成，每人有10幅不同的图像，每幅图像均具有1 440×900的128级灰度。这些图像是在5种不同表情或姿态下拍摄的，如图1所示。

图1 CBR人脸库Fig.1 Library of CBR faces

先根据权值选择方法对人脸数据库进行权值计算。将人脸库这5幅图像用权值选择算法分别计算，这样共计算10次，取平均值，最后得到眉、眼、鼻子以及嘴这4个关键局部的权值分别为0.201，0.283，0.216，0.300，全局极值设置为1。根据上面研究得到的权值，对本文算法进行验证。为了验证本文算法的效果，实验比较了3种不同的人脸识别算法：Eigenface算法、Fisherface算法[11-12]和本文提出的加权 PCALDA算法。每次对100个实验样本进行识别，最后给出每组实验的识别率。3种算法的识别效果比较结果见表1。

表1 3种算法的识别率比较Table 1 Recognition effect comparison of three kinds of algorithms

由表1可以看出：Eigenface算法的平均识别率为85.0%，传统Fisherface算法的平均识别率为90.6%，本文算法的平均识别率高达 97.0%，充分证明了本文算法的有效性。再次，提取不同特征来验证本文算法中特征融合的思想，进行若干次实验，每次实验提取不同的样本特征，如全局特征、单个局部特征、组合局部特征、多区域融合特征等，采取本文提出的加权PCA-LDA算法，所得实验结果如表2所示。

由表2可知：将人脸全局特征和局部特征进行有效综合并再进行人脸识别，其效果要比单一的特征提取效果明显提高。研究结果表明：若将人脸的全局特征和局部特征进行有效融合后再进行人脸识别，将有效地提高人脸识别正确率。

表2 采用不同样本特征向量的识别效果比较Table 2 Recognition effect comparison about different sample characteristic vectors

5 结论

(1)以人脸识别为例，给出了 1种基于样本加权特征矩阵和类矩阵的自适应PCA-LDA弱目标识别方法，并据此设计了样本加权特征矩阵来代替传统的特征向量，有效地将局部和全局特征加权融合。定义了每类样本的类矩阵，解决了 LDA算法小样本空间问题。

(2)PCA-LDA算法能很好地结合图像全局和局部的互补信息，其识别效果优于各单一区域的分类效果；计算速度较快，且平均识别率高达 97.0%，有效性和鲁棒性好。

(3)该方法可以应用到其他弱目标如车牌识别系统中，为提高其他弱目标的识别率提供了一种有效的方法。

[1] Chellappa R, Wilson C L, Sirohey S. Human and machine recognition of faces: A survey[C]//Proceedings of the IEEE.New York: The Haworth Press, 1995: 735-741.

[2] Kotropoulos C L, Tefas A, Pitas I. Frontal face authentication using discriminating grids with morphological feature vectors[J].IEEE Transactions on Multimedia, 2000, 2(1): 14-26.

[3] Tefas A, Kotropoulos C, Pitas L. Using support vector machine to enhance the performance of elastic graph matching for frontal face authentication[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(7): 735-746.

[4] 杨欣. 自动人脸识别若干关键问题研究[D]. 南京: 东南大学自动化学院, 2006.YANG Xin. Study of some key issues of automatic face recognition[D]. Nanjing: Southeast University. School of Automation, 2006.

[5] Jonsson K, Kitier J, LI Yong-ping, et al. Support vector machines for face authentication[J]. Image and Vision Computing, 2002, 5(6): 369-375.

[6] Turk M, Pentland A. Eigenfaces for recognition[J]. Journal of Cognitive Neuroscience, 1991, 3(1): 71-86.

[7] Belhumeur V, Hespanda J, Kiregeman D. Eigenfaces versus fisherfaces: Recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1997, 19(7): 711-720.

[8] Yu H, Yang J. A direct LDC algorithm for high dimensional data with application to face recognition[J]. Journal of Pattern Recognition, 2001, 34(10): 2067-2070.

[9] Bing Y, Ianfu J L, Ping C. A new LDA-based method for face recognition[C]//Proceedings of 16th International Conference Pattern Recognition. New York: The Haworth Press, 2002:168-171.

[10] Bartlett M S, Movellan J R, Sejnowski T J. Face recognition by independent component analysis[J]. IEEE Transactions on Neural Networks, 2002, 13(6): 1450-1464.

[11] Moghaddam B. Principal manifolds and probabilistic subspaces for visual recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(6): 780-788.

[12] Kim K L, Jung K, Kim H J. Face recognition using kernel principal component analysis[J]. IEEE Signal Processing Letters,2002, 9(2): 40-42.

[13] Mika S, Ratsch G, Weston J, et al. Fisher discriminant analysis with kernels[C]//Proceedings of IEEE Workshop on Neural Network Signal Processing. New York: The Haworth Press,1999: 41-48.

[14] Martinez A, Kak A. PCA versus LDA[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(2):228-233.

[15] Pentland A, Moghaddam B. Starner view-based and modular eigenspaces for face recognition[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. New York: The Haworth Press, 1994: 84-91.

[16] WANG Yun-hong, FAN Wei, TAN Tie-niu. The subspace face recognition algorithm about fusion of the overall situation and the partial characteristic[J]. Journal of Computers, 2005, 28(10):1657-1663.