一种低碳微合金管线钢的热变形行为

林武，李红英，曾翠婷，宾杰，魏冬冬

(中南大学 材料科学与工程学院，湖南 长沙，410083)

热变形工艺对保证钢铁材料组织的性能至关重要，热变形过程中流变应力是决定变形所需载荷及消耗能量的关键因素，是材料在高温下的基本性能指标之一。国内外科技工作者对铝合金、低合金结构钢、不锈钢等的高温变形特性进行了大量的研究，建立了相应的热变形流变应力模型[1-3]。在现代塑性加工力学中，精确的流变应力表达式是提高理论计算精度的关键[4-6]。低碳微合金中厚钢板广泛应用于输送石油、天然气的管道建设中，对于X70及以上强度级别的管线钢，要求其显微组织以针状铁素体为主[7]，要获得良好的综合力学性能，必须在生产中采用控冷控轧(TMCP)工艺[8]，因此，研究低碳微合金管线钢的热变形特性和建立流变应力模型具有重要的工程价值。在钢材的热轧过程中，加工硬化、动态回复、动态再结晶等会同时发生[9]，为了在生产中实现钢材的奥氏体区轧制，必须对热变形及其组织演变行为进行研究，确定其发生再结晶的条件，建立流变应力模型，预测不同工艺条件下变形抗力的变化情况。目前，人们对X70管线钢热变形奥氏体的静态再结晶行为进行了研究[10]，但是，关于低碳微合金管线钢在变形过程中的动态再结晶行为的研究还未见报道。流变应力在一定程度上反映了材料微观组织的变化，人们能够根据钢的组织性能较好地预测钢的高温变形行为[11]。本文作者在MMS-200热力模拟机上采用圆柱体高温压缩实验方法，研究一种X80钢级的低碳微合金管线钢热压缩的力学行为，建立流变应力模型，研究实验钢热变形条件和变形组织的关系。

1 实验

实验所用钢材取自用于轧制X80管线钢的粗轧板坯，化学成分(质量分数)见表1。

表1 实验钢的化学成分Table 1 Composition of tested steel %

在MMS-200热力模拟实验机进行单道次压缩热模拟实验，将直径×高为8 mm×15 mm的试样以10 ℃/s加热至1 200 ℃，保温5 min后，以10 ℃/s分别冷至变形温度为1 150，1 000，900和800 ℃，保温20 s，工程应变60%，变形速率ε˙分别为0.1，1.0，5.0 s-1，以20 ℃/s的速度冷却至室温，采集数据，用origin8.0软件绘制出相应的真应力(σ)与真应变(ε)的关系曲线。

用 POLYVER-MET金相显微镜观察试样的金相组织，采用TecnaiG220透射电子显微镜进行微观组织观察，加速电压为200 kV。

2 结果与分析

2.1 热变形行为

2.1.1 真应力-真应变曲线

图1所示为同一变形速率下不同变形温度的真应力-真应变曲线，变形速率分别为0.1，1.0和5.0 s-1，由图1可知：在同一应变速率下，真应力随着变形温度的升高而降低。由图 1(a)可以看出：在低应变速率(0.1 s-1)下，800，900和1 000 ℃的流变应力曲线表现出动态回复特征，真应力-真应变曲线明显分为3个阶段(第1阶段为微变形阶段，随着变形量的增加，真应力迅速提高；产生屈服后，变形进入第2阶段，加工硬化率逐渐降低；第3阶段为稳态变形阶段，流变应力增加到1个峰值后趋于稳定，加工硬化与动态软化达到动态平衡)。由图1(b)和(c)可见：变形温度为1 100℃及其以下温度的流变应力曲线也属于动态回复型曲线，真应力随着应变量的增加持续升高；当应变速率较低时，1 150 ℃的流变应力曲线表现出明显的动态再结晶特征，真应力达到峰值后随着应变量的增加而逐渐下降；当应变速率较高时，1 150 ℃时的流变应力曲线出现稳态流变阶段。

图1 同一变形速率下不同变形温度的真应力(σ)-真应变(ε)曲线Fig.1 σ-ε curves with same strain rate but different deformation temperatures

流变应力曲线不仅能反映材料变形的力学行为，还能反映变形过程中的组织变化，流变应力与亚晶、亚晶粒取向差和位错密度直接相关。高温塑性变形时存在着硬化和软化2个过程，位错增殖引起加工硬化，位错相消和重排引起动态软化。在变形初期，位错交滑移引起的软化不足以补偿位错密度增加引起的硬化，因此，真应力逐渐增大；随着应变量的增大，材料内部空位浓度逐渐提高，达到一定变形程度后，刃位错开始攀移，材料的软化程度提高，硬化和软化的平衡向低硬化指数方向发展，真应力随着真应变增加的趋势减缓，最终，真应力达到峰值。当位错交滑移、攀移和位错脱钉等引起的软化与应变硬化达到动态平衡时，真应力-真应变曲线接近于水平线，变形进入稳态流变阶段，应力达到峰值后，如果软化程度超过硬化，真应力持续降低。

图2所示为相同变形温度下不同变形速率的真应力-真应变曲线，其中：σ为真应力，MPa；ε为真应变。由图2可以看出：同一变形温度下，真应力随应变速率的增大而增大，表明实验钢是正应变速率敏感材料；热加工时，随着应变速率降低，单位应变的变形时间增加，软化能更充分地进行，使得峰值应力随应变速度的降低而降低。应变速度ε˙与流变应力σ之间是一种复杂的非线性关系，当应变速率较大时，在实验变形量范围内，峰值应力消失。

图2(a)～(c)所示分别对应800，900和1 000 ℃时的真应力-真应变曲线，呈现动态回复型流变应力特征，只在对应速率为0.1 s-1时才出现了稳态变形阶段，对应其他变形速率，随着应变量的增加，真应力持续上升。图2(d)显示：当变形温度升高到1 150 ℃时，对应较高的变形速率(5.0 s-1)的流变应力曲线呈现动态回复型特征，出现了近似稳态的变形阶段，对应0.1 s-1和1.0 s-1的变形速率，流变应力出现峰值后持续下降，表明发生了动态再结晶。

图2 同一变形温度下不同变形速率的真应力(σ)-真应变(ε)曲线Fig.2 σ-ε curves with same deformation temperature but different strain rates

表2所示为在不同变形温度和应变速度条件下的峰值应力。由表2可以看出：随着变形温度的升高和应变速率的降低，峰值应力降低，以1 150 ℃和0.1 s-1变形条件的流变应力最低，仅为54 MPa；当应变速度不变时，真应力随着温度升高而降低，当应变速度为0.1 s-1时，800 ℃时的峰值应力为248 MPa，在900 ℃时峰值应力降至184 MPa；当变形温度不变时，峰值应力随着应变速度的增大而增大，在1 000 ℃变形时，当应变速度由0.1 s-1提高到5.0 s-1时，峰值应力由144 MPa提高到207 MPa。这是因为随着变形温度的升高和应变速度的降低，基体中的自扩散、刃型位错的攀移、螺型位错的交滑移得以充分进行，大量位错互相抵消，位错密度大大减少，软化程度增大。

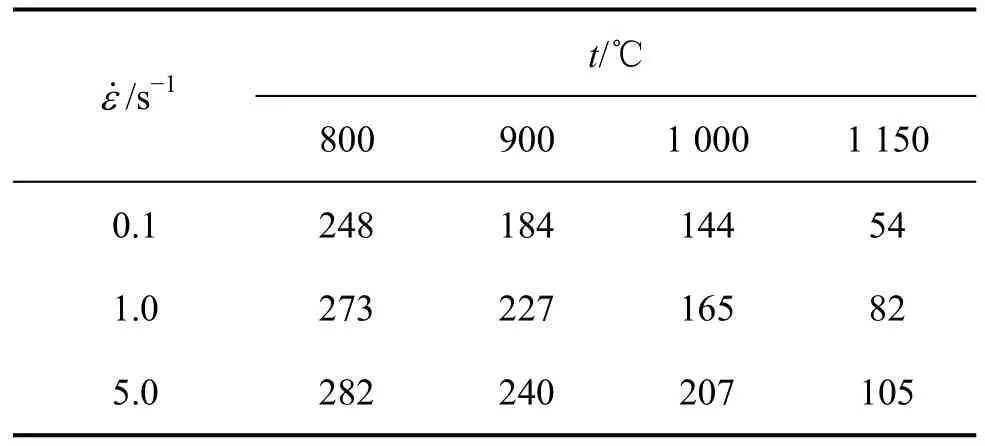
表2 不同变形温度和应变速度对应的峰值应力(εp)Table 2 Peak stress at different deformation temperatures and strain rates MPa

2.1.2 热变形组织

图3所示为实验钢以不同变形温度和不同变形速率实现60%工程应变的金相组织。当变形温度为800℃和900 ℃时，其变形组织为多边形铁素体和粒状贝氏体，多边形铁素体体积分数较大；当变形温度为1 000 ℃时，显微组织为针状铁素体、粒状贝氏体和少量多边形铁素体，变形速率增大，针状铁素体质量分数增大；当变形温度为1 150 ℃时，其显微组织为针状铁素体、多边形铁素体、粒状贝氏体。由图3可以看出：随着变形速率的增大，针状铁素体含量增加，特征更明显，组织细小、均匀。较低变形速率的粒状贝氏体较大，而对应较高应变速率的组织，由于晶界两边板条铁素体位向差别较大，使得晶界处易被腐蚀，呈黑色。

2.2 流变应力方程

2.2.1 流变应力表达式

在不同应力下，流变应力σ、应变速度ε˙和变形温度T之间的关系可用不同公式表示：当应力较低时，关系式用式(1)表示；当应力较高时，关系式用式(2)表示；在整个应力范围内，可用式(3)表示[12]。大量研究表明：式(3)较好地描述了常规的热加工变形，可用来描述热激活稳态变形行为，还可用于估算热变形激活能Q。

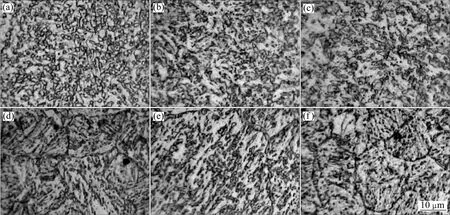
图3 不同变形温度和变形速率条件下的显微组织Fig.3 Microstructures at different deformation temperatures and strain rates

式中：σ为峰值应力或稳态流变应力，或某指定应变对应的流变应力；R为摩尔气体常数；Q为变形激活能；T为热力学温度；A，α和n为与温度无关的常数，其中n为应力指数，α为应力水平参数。一般地，A在高应力水平时为与速度控制机制中热激活位置成正比的结构因子，与变形材料内部激活位置密度、空位浓度、位错割阶的平均间距、位错柏氏矢量、原子配位数、跃迁频率以及激活熵等有关。当应力降低时，A，α和n的物理意义也发生变化。

高温塑性变形存在热激活过程，Zener和Hollomon引入Z参数的概念[13]，用式(4)表达，其物理意义是温度补偿的变形速率因子，依赖于T而与σ无关。若已知与试验结果相符的经验公式Z=f(σ)，则可以测定与σ无关的热变形激活能。

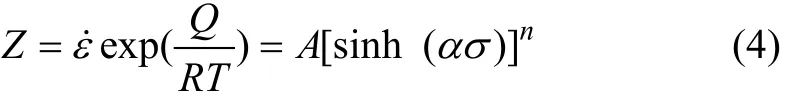
在热变形过程中，钢的高温流变应力σ主要取决于变形温度和应变速率，可用式(5)表达，σ可表达成Z参数的函数：

只要已知A，α，n和Q等材料常数，便可由式(5)求得材料在任意变形条件下的流变应力，即可利用该式计算材料热加工过程中流变应力与应变速度、温度等的关系，为制定热加工工艺参数提供依据。若Z不变，则材料稳态流变阶段的组织特征不会发生明显变化，由此就可以建立材料组织和性能与热变形工艺之间关系的预测模型。

2.2.2 材料常数的求解

对式(1)～(3)两边取对数，分别得到式(6)～(8)。

对式(8)求偏导数，得：

大量研究结果表明：峰值应力和稳态流变应力满足一定的线性关系，且峰值应力和稳态流变应力都能较好地用Z参数函数形式来描述[14-15]，对工业应用而言，获得峰值应力与温度及应变速率的关系更为重要。取流变应力为峰值应力，将表2中数据代入式(6)和式(7)，描点后进行线性回归，得到 ln- l nσ和ln-σ回归直线，如图4所示。n1和β可取4条直线斜率的平均值，得n1=14.73，β=0.078，求出α=β/n1=0.005。

将不同变形温度的峰值应力和应变速度代入式(8)，应用最小二乘法进行线性回归，所得结果如图5和图6所示。表3所示为4个变形温度对应直线的斜率ni，平均斜率n=10.796；表4所示为3种变形速率对应直线的斜率bi，平均斜率b=6.376。

将得到的n和b代入式(9)，求得平均变形激活能Q为 572.30 kJ/mol，将Q代入式(4)，得到Z=对式(4)两边求对数，得：

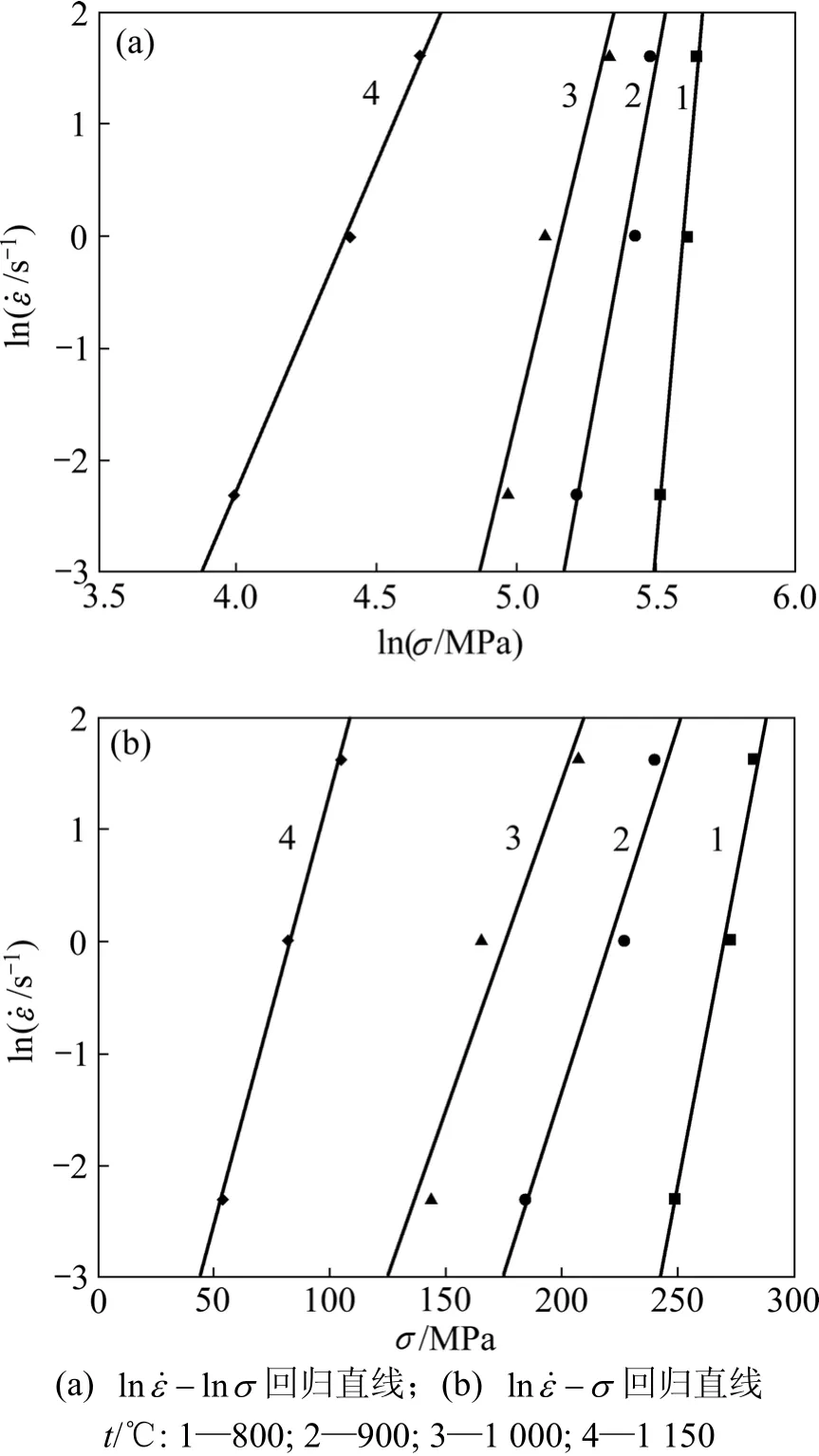
图4 实验钢峰值应力与应变速度之间的关系Fig.4 Relationships between peak stress and strain rate of X80 steel

图5 峰值应力σ与应变速度的关系Fig.5 Relationships between peak stress and strain rate

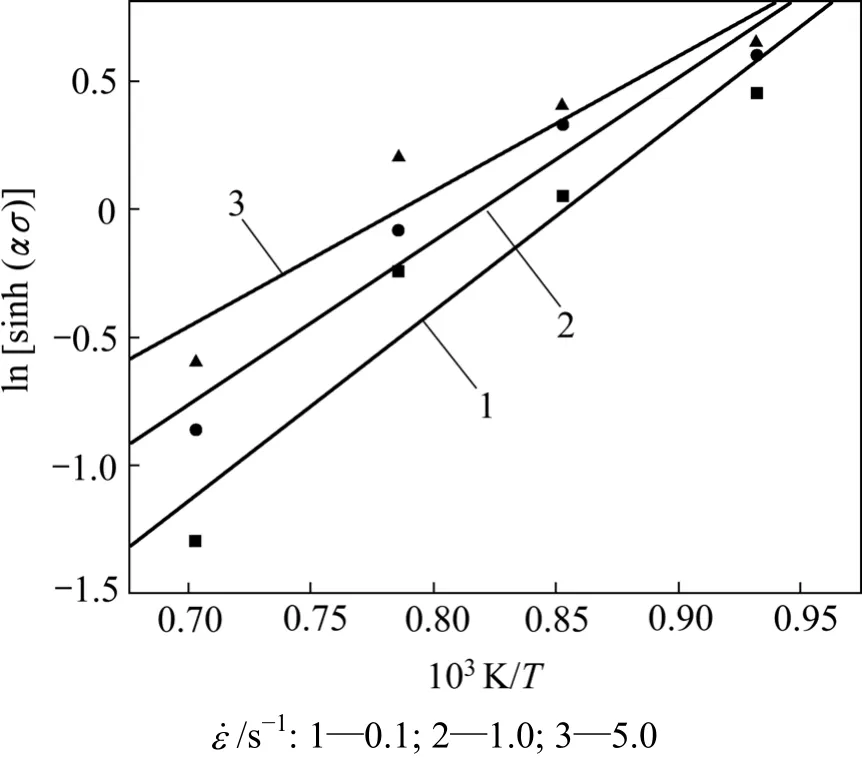
图6 峰值应力σ与温度的关系Fig.6 Relationships between peak stress and temperature

表3 l n[sinh (α σ)] 与 ln ˙的直线关系的斜率niTable 3 Slope ni of linear between l n[sinh (α σ)] and l n

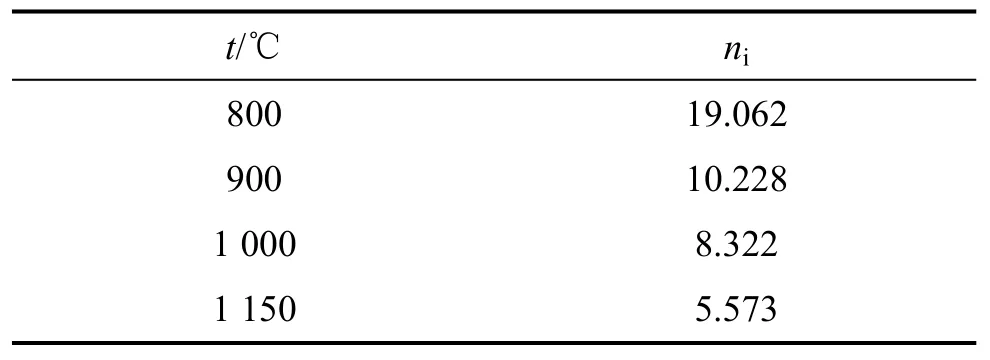
表3 l n[sinh (α σ)] 与 ln ˙的直线关系的斜率niTable 3 Slope ni of linear between l n[sinh (α σ)] and l n

t/℃ ni 800 19.062 900 10.228 1 000 8.322 1 150 5.573

表4 103 K/T和 ( )]ln[sinhασ 的直线关系的斜率biTable 4 Slope bi of linear between 103 K/T and ( )]ln[sinhασ

为使结果更为精确，进行迭代计算，将n代入α=β/n求得新的α，再利用该n和α进行迭代求其他材料常数。经过几次迭代后，求得材料常数为：n=5.73，α=0.012 MPa-1，A=2.6×1018s-1，Q=518.73 kJ/mol。把各常数代入式(5)，得到式(11)所示的流变应力方程，峰值应力与应变速率、温度的关系可用参数Z表示。其中：

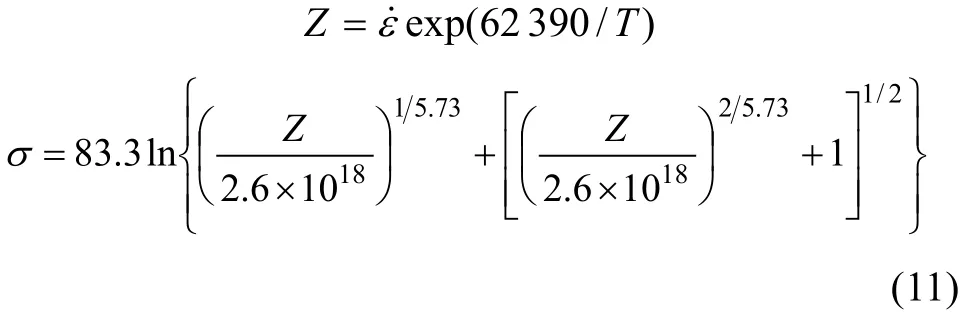
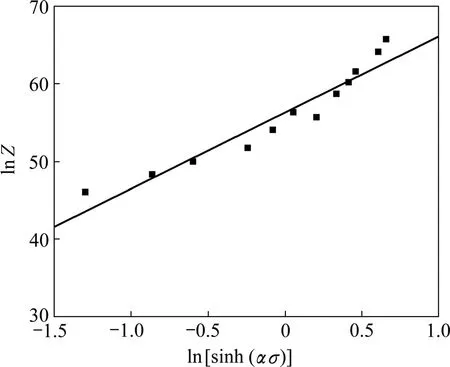
图7 流变应力与Z的关系Fig.7 Line relationship between flow stress and parameter Z

3 动态回复和动态再结晶

图8所示为利用透射电镜观察到的不同变形条件的微观组织。由图8(a)可见：在900 ℃和1.0 s-1变形条件下，位错密度很高，产生了位错缠结；在1 150 ℃和 5.0 s-1变形条件下，为典型的回复组织(图8(b))；在1 150 ℃和0.1 s-1变形条件下，出现了三叉晶界，表明已经发生动态再结晶(图8(c))。由图8(d)可见：再结晶后显微组织以针状铁素体为主，板条铁素体间，有少量奥氏体(A)残留下来，以岛的形式分布于板条间和大角度晶界处，岛内的成分主要是碳，合金元素与基体相近，成为富碳奥氏体岛，在冷却过程中，大部分奥氏体转变为马氏体(M)，形成M/A岛。

图8 不同温度和变形速度条件下的TEM像Fig.8 TEM images at different temperatures and deformation rates

已有研究表明：针状铁素体组织由带有高位错密度的板条铁素体晶体组成，若干铁素体板条平行排列构成板条束，板条界为小角度晶界，其形态细长；板条束界面则为大角度晶界，针状铁素体具有非常细的亚结构、高的位错密度、良好的组织均匀性和较小的等效晶粒尺寸。在针状铁素体中，裂纹在扩展中不断受到彼此咬合以及相互交错分布的针片状条束的阻碍，对解理断裂具有高抗力，因此，具有优良的力学性能。细小而不连续分布的M/A岛也不易激发裂纹，不易提供连续的裂纹扩展通道。

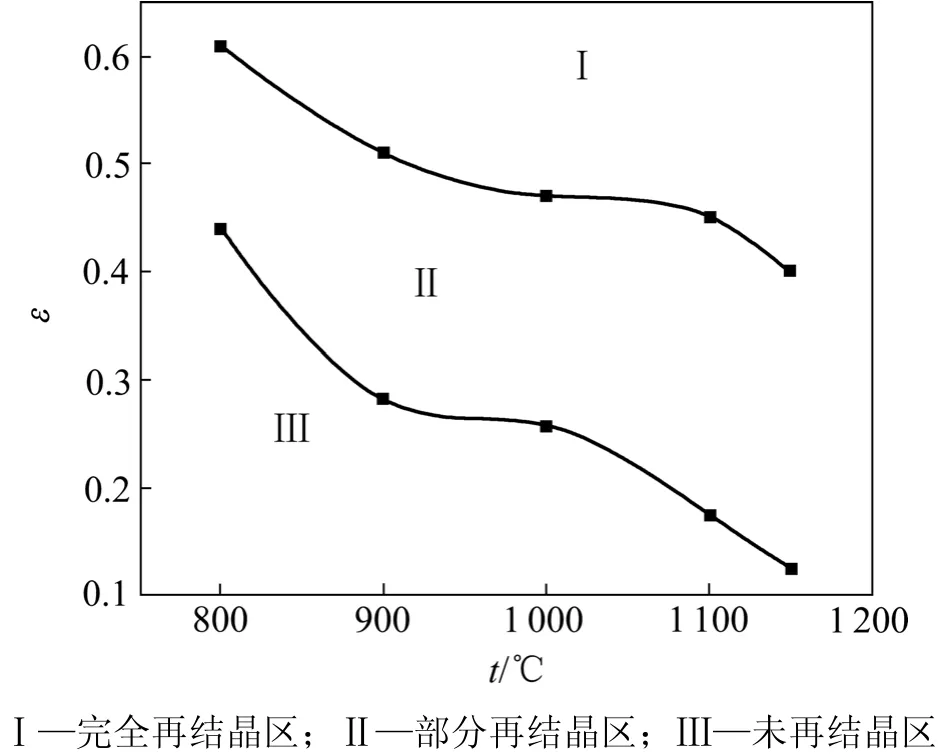
图9 变形速率为0.1 s-1的动态再结晶动力曲线Fig.9 Diagrams of dynamic recrystallization with stain rate of 0.1 s-1

图9 所示为实验钢在0.1 s-1变形速率下的动态再结晶动力曲线。由图1和图9可以看出：在一定的应变速率下，随着变形温度的降低，峰值应力向应变增加的方向移动，即峰值应力对应的应变增大，开始发生动态再结晶的临界应变也增大，需要较大的变形量才能发生动态再结晶。由图9可以看出：Ⅰ区为完全再结晶区；Ⅲ区为未再结晶区；Ⅱ区为部分再结晶区。为了消除混晶现象，要避免在Ⅱ区变形。合金元素的加入显著推迟基体金属的动态再结晶过程，实验钢含有较高的Mn，Mo和Cu等合金元素含量，使得实验钢的热变形激活能比X65钢的热变形激活能大很多，合金元素还可通过影响晶界迁移来影响动态再结晶过程。因此，低碳微合金钢在相同变形量下发生动态再结晶的临界变形量较大。

4 结论

(1)在800～1 150 ℃和0.1～5.0 s-1的应变速率范围内，实验钢的流变应力随着变形温度的升高而降低，随着应变速率的提高而增大。

(2)可采用Zener-Hollomon参数的双曲正弦函数来描述实验钢高温变形的峰值流变应力，计算得到材料常数α=0.012 MPa-1，n=5.73，A=2.6×1018s-1，变形激活能Q=518.73 kJ/mol。峰值流变应力与应变速率、温度的关系可用由Z参数表示的流变应力方程表达：

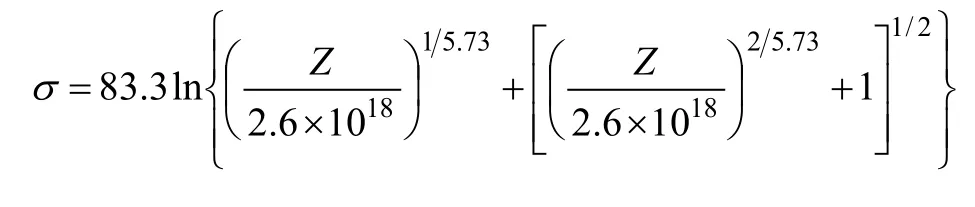
(3)在本研究的变形条件下，当变形温度为1 150℃及变形速率为0.1 s-1时，发生了明显的动态再结晶；当变形温度小于1 150 ℃和变形速率大于1.0 s-1时，金属以动态回复为主要的软化机制。

[1] 王立民, 张红, 吕成林, 等. 0Cr11Ni2MoVNb钢高温压缩变形的流变应力[J]. 金属热处理, 2008, 33(10): 74-76.WANG Li-min, ZHANG Hong, LÜ Cheng-lin, et al. Compress deformation flow stress of 0Cr11Ni2MoVNb steel at high temperature[J]. Heat Treatment of Metals, 2008, 33(10): 74-76.

[2] 刘战英, 陈连生, 周满春, 等. 变形条件对 30MnSiV 钢动态再结晶行为的影响[J]. 钢铁研究学报, 2004, 16(1): 49-52.LIU Zhan-ying, CHEN Lian-sheng, ZHOU Man-chun, et al.Effect of deformation conditions on dynamic recrystallization of 30MnSiV[J]. Journal of Iron and Steel Research, 2004, 16(1):49-52.

[3] 韩冬峰, 郑子樵, 蒋呐, 等. 高强可焊 2195铝锂合金热压缩变形的流变应力[J]. 中国有色金属学报, 2004, 14(12):2090-2095.HAN Dong-feng, ZHENG Zi-qiao, JIANG Na, et al. Flow stress of high-strength weldable 2195 aluminium-lithium alloy during hot compression deformation[J]. The Chinese Journal of Nonferrous Metals, 2004, 14(12): 2090-2095.

[4] Bardi F, Cabibbo M. An analysis of hot deformation of an Al-Cu-Mg alloy produced by powder metallurgy[J]. Material Science and Engineering A, 2003, 339(1/2): 43-52.

[5] Akira Y, Jun Y. A novel approach to determine the kinetics for dynamic recrystallization by using the flow curve[J]. Journal of Materials Processing Technology, 2004, 151(1/3): 33-38.

[6] Cavaliere P. Hot and warm forming of 2618 aluminium alloy[J].Journal of Light Metals, 2002, 4(2): 247-252.

[7] 王春明, 吴杏芳, 刘玠, 等. X70针状铁素体管线钢析出相[J].北京科技大学学报, 2006, 28(3): 253-258.WANG Chun-ming, WU Xing-fang, LIU Jie, et al. Precipitates in X70 pipeline steel[J]. Journal of University of Science and Technology Beijing, 2006, 28(3): 253-258.

[8] 江海涛, 康永林, 于浩, 等. 用炉卷轧机生产高强韧管线钢的生产技术[J]. 钢铁研究学报, 2006, 18(3): 1-5.JIANG Hai-tao, KANG Yong-lin, YU Hao, et al. Production technology of high strength and toughness pipeline steel produced by Steckel mill[J]. Journal of Iron and Steel Research,2006, 18(3): 1-5.

[9] 熊家强, 谢刚, 唐广波. 304不锈钢热变形过程奥氏体动态再结晶及流变应力研究[J]. 云南冶金, 2008, 37(5): 37-42.XIONG Jia-qiang, XIE Gang, TANG Guang-bo. Research on dynamic recrystallization of austenite and flow stress during hot deformation process of 304 stainless steel[J]. Yunnan Metallurgy,2008, 37(5): 37-42.

[10] 陈庆军, 康永林, 孙浩, 等. X70管线钢热变形奥氏体的静态再结晶行为[J]. 北京科技大学学报, 2007, 29(12): 1212-1215.CHEN Qing-jun, KANG Yong-lin, SUN Hao, et al.Static-recrystallization behavior of hot deformation austenite in X70 pipeline steel[J]. Journal of University of Science and Technology Beijing, 2007, 29(12): 1212-1215.

[11] Pietrzyk M. Through-process modelling of microstructure evolution in hot forming of steels[J]. Journal of Materials Processing Technology, 2002, 125/126: 53-62.

[12] Cho S H, Kang K B, Jonas J J. Mathematical modeling of the recrystallization kinetics of Nb microalloyed steels[J]. The Iron and Steel Institute of Japan International, 2001, 41(7): 766-773.

[13] 王有铭, 李曼云, 韦光. 钢材的控制轧制和控制冷却[M]. 北京: 冶金工业出版社, 1995: 20-22.WANG You-ming, LI Man-yun, WEI Guang. The control rolling and cooling for steel[M]. Beijing: Metallurgical Industry Process,1995: 20-22.

[14] Sakai T. Dynamic recrystallization microstructures under hot working conditions[J]. Journal of Materials Processing Technology, 1995, 53: 349-361.

[15] 虞毅, 高惠临, 霍春勇, 等. X70管线钢管件制造热过程中的形变规律[J]. 机械工程材料, 2006, 30(5): 17-19.YU Yi, GAO Hui-lin, HOU Chun-yong, et al. Deformation law in fitting-manufacture thermal process of X70 pipeline steel[J].Materials for Mechanical Engineering, 2006, 30(5): 17-19.