电液位置伺服系统的规则自校正模糊PID控制器

邵俊鹏，王仲文，李建英，韩桂华

(哈尔滨理工大学 机械动力工程学院，黑龙江 哈尔滨，150080)

电液位置伺服系统具有响应速度快、控制精度高、动态位置刚度和稳态刚度大、抗干扰能力强等优点，被广泛应用于各种工业过程控制领域[1]。但是，液伺服系统是典型的非线性系统，存在不确定性、时变性、外界干扰和交叉耦合干扰，另外还受到如油液黏度、温度、现场工况等多种参量因素的影响[2-3]。采用传统的PID算法时，控制参数选择较困难，系统存在抗干扰能力低、超调量大等缺点；若只采用模糊控制算法，虽然能避免PID算法的某些不足，但仍存在稳态精度较低，动态性能欠佳，控制效果也很不理想等缺点[4-5]。模糊PID控制算法将模糊控制和PID控制相结合的方法，模糊控制规则在线调整PID控制器参数，构成模糊变系数PID控制器，既可以保留PID控制器没有静差的特点，又能获得模糊控制鲁棒性强的优点。然而，模糊控制规则是根据人们的经验总结出来的，往往具有一定的片面性，普通模糊控制器的控制规则一旦确定便不能改变，这就不能很好地适应系统动态特性的变化或随机干扰的影响，从而影响模糊控制的效果[6-8]。为此，本文作者在研究模糊 PID控制器的基础上，对模糊控制器的结构进行改进，提出一种基于模糊控制规则自校正的模糊PID复合控制算法；利用实时工作间(RTW)的半物理仿真环境和 MATLAB系统辨识工具箱，对电液位置伺服系统进行模型辨识；以辨识的模型为对象设计出电液位置伺服系统规则自校正模糊PID控制器，并在MATLAB下进行数字仿真。

1 电液位置伺服系统的系统描述

电液位置伺服系统原理方框图如图1所示。此系统是典型的阀控对称缸系统，主要由控制器、放大器、伺服阀、液压缸和位置传感器等组成。电液伺服阀的额定压力为21 MPa；额定流量为30 L/min；液压缸的额定压力21 MPa，行程为正负100 mm；负载为750 N；负载刚度K为115～5 000 N/mm。图1中，R为给定值，Y为液压缸的位移。计算机向伺服阀输入控制信号，与位移传感器反馈信号进行比较，差值经控制器处理、放大给伺服阀以电流信号控制其开口，通过伺服阀的流量变化来控制液压缸的位移，实现位置闭环控制。

根据液压控制理论可推导电液位置伺服系统的数学模型，系统的简化传递函数为：

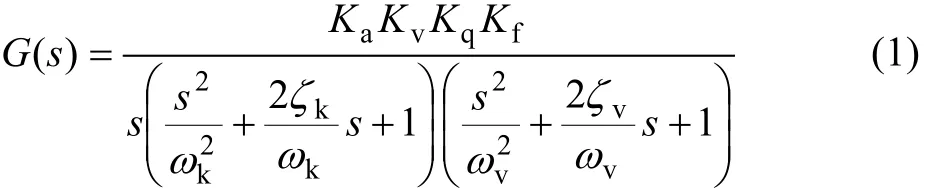
式中：Ka为伺服放大器比例增益；Kv为电液伺服阀流量增益；Kq为液压伺服缸的流量增益；Kf为位移传感器的电压-位移比例环节；ωk为液压缸液压固有频率；ξk为液压缸液压阻尼比；ωv为电液伺服阀的固有频率；ξv为伺服阀阻尼比；s为系统的传递函数。

2 基于MATLAB的模型辨识

系统模型辨识是在伺服系统试验并获得实测输入和输出数据的基础上，进行必要的数据处理和计算，估计出一个与所测系统等价数学模型的过程[9]。

经大量的试验采集到系统输入输出数据，在MATLAB环境下把采集到的数据导入，进行预处理，数据被分成2部分：一部分作为工作数据进行模型辨识，另一部分作为验证数据。辨识模型采用 ARX模型和状态空间模型，获得的电液位置伺服系统的辨识模型闭环传递函数为：

取反馈系数为 1，根据反馈系统传递函数之间的关系，可得辨识模型的开环传递函数为：

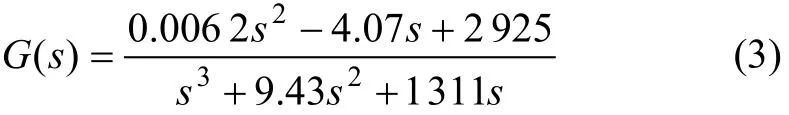
模型辨识得到的系统开环传递函数需要验证。因电液伺服系统具有典型的非线性特点，因此，验证模型辨识的正确性时，需要在不同工况下多次实验，记录多组数据。在离线条件下对辨识模型进行仿真，然后，在电液位置伺服系统试验台上进行实验，输入信号为正弦波，幅值为1，频率为1 Hz，所得辨识模型的验证曲线如图2所示。可见：系统试验与辨识模型的正弦信号响应曲线几乎重合。不同工况下的多次实验都说明辨识的模型是可信的。

图1 电液位置伺服系统组成图Fig.1 Diagram of electro-hydraulic position servo system

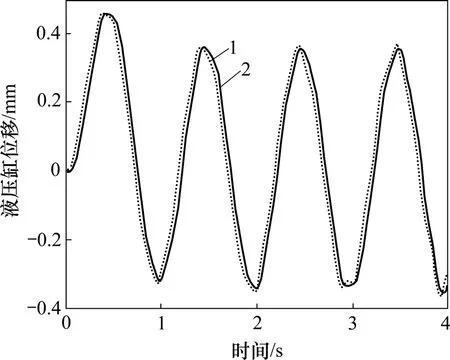
图2 辨识模型的验证曲线Fig.2 Validation curves of identification model

3 控制器设计

3.1 规则自校正模糊PID控制器的设计

规则自校正模糊PID控制器的主要任务就是找出PID 3个参数与e和ec之间的模糊关系，在运行中通过不断检测偏差e、偏差变化ec和自校正因子α，根据模糊控制原则对3个参数进行在线修改。模糊PID控制器将模糊控制和PID控制相结合，利用模糊控制的快响应和超调量小以及PID的精度高的特点，采用二级控制的方法，提高系统的性能[10-12]，规则自校正fuzzy-PID控制器的结构如图3所示。

PID控制器采用位置式数字PID算法，其传递函数为：

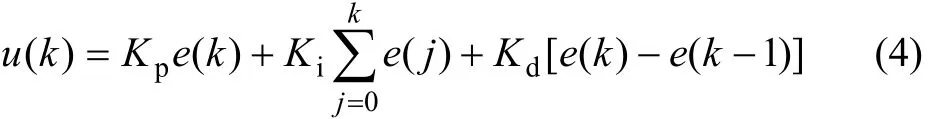
式中：Kp为比例系数；Ki为积分系数；Kd为积分系数；e(k)为系统误差。Kp，Ki和Kd的整定采用试凑法，得到PID 3个控制参数的初始值Kp0，Ki0和Kd0。

3.2 自校正因子模糊控制器的设计

模糊控制器的结构采用两输入三输出的基本形式。输入变量采用液压缸位移的偏差e以及偏差的变化ec，输出变量为3个自校正因子α1，α2和α3。设偏差和偏差变化的模糊论域E和EC均取为[-3，+3]，语言变量值均为{NB(负大)，NM(负中)，NS(负小)，ZO(零)，PS(正小)，PM(正中)，PB(正大)}={-3，-2，-1，0，1，2，3}；自校正因子α1，α2和α3的论域取为[0，1]，语言变量值均为{VB(较大)，MB(中大)，B(大)，S(小)，MS(中小)，VS(较小)}={1，0.8，0.6，0.4，0.2，0}。隶属函数曲线如图4所示。

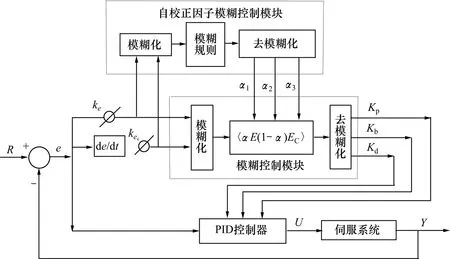
图3 fuzzy-PID控制器结构图Fig.3 Diagram of fuzzy-PID controller

图4 模糊集输入/输出变量隶属函数曲线Fig.4 Memberships curves of inputs/output to Fuzzy set

模糊控制规则是模糊控制的核心，根据专家知识，参照模糊自校正因子取值主要原则可以归纳出如图5所示的基本模糊控制规则。应用Mamdani直接推理法和“极大-极小”法则进行模糊关系的合成运算，并采用重心法进行反模糊化，可以得到自校正因子的基本模糊控制策略。

图 3中的ke和kec分别是偏差e的量化因子和偏差变化ec的量化因子，偏差e和偏差变化ec的模糊论域都为[-3，+3]，基本论域分别为[-0.6，+0.6]，[-60，+60]，故ke和kec的初始值分别为ke=3/0.6=5，kec=3/60=0.05，用小的增量一步一步地对ke和kec进行参数优化，优化的目标是使系统具有“快速-无超调”的阶跃响应特性。采用 ITAE准则，参数优化的目标函数为：

式中：J为误差函数与时间的积分；t为仿真时间。

4 仿真研究

4.1 基于MATLAB的仿真

为了验证电液位置伺服系统规则自校正模糊 PID控制器的性能，利用MATLAB的Simulink工具对其进行仿真分析，控制器的仿真模型如图6所示。以模型辨识获得的开环传递函数为控制对象，输入单位阶跃信号，分别对常规线性PID控制器、模糊PID控制器以及规则自校正 fuzzy-PID控制器进行仿真，获得单位阶跃响应结果如图7所示。传统PID控制器阶跃响应调整时间为1.4 s；fuzzy-PID控制器阶跃响应上升时间为0.45 s，调整时间为0.5 s，与常规PID控制系统相比，其系统的快速性明显提高，但存在一定的稳态误差。

规则自校正 fuzzy-PID控制器综合考虑了系统的快速性和稳态精度，上升时间为0.24 s，调整时间为0.20 s，从输出曲线可以看出：系统响应速度加快，振荡幅度减小而且很快衰减至稳态，基本没有稳态误差。

4.2 半物理仿真分析

根据受控对象的数学模型，在离线状态下设计的控制器，仿真结果只是针对数学模型得出的纯数字结果，若将这种控制器进行硬件实现，直接用于实际受控对象的控制，就不一定能得到满意的控制效果，甚至未造成系统损坏，因此，半物理仿真方法显得非常重要。将受控对象放置在仿真系统中进行仿真，即为硬件在回路的仿真。因为设计出来的控制器可以直接对实际受控对象进行控制，所以，可以得出对其控制效果的评价[13]。半物理仿真系统采用 xPC Windows Targets，宿主机为PC机，用于运行Simulink，设计、创建控制器；目标机为研华工控机，通过输入输出接口卡以及数据线将实际的受控对象和宿主机连接起来，成为一个实时系统。

图6 规则自校正fuzzy-PID控制器的仿真模型Fig.6 Simulink model of self-tuning fuzzy-PID controller

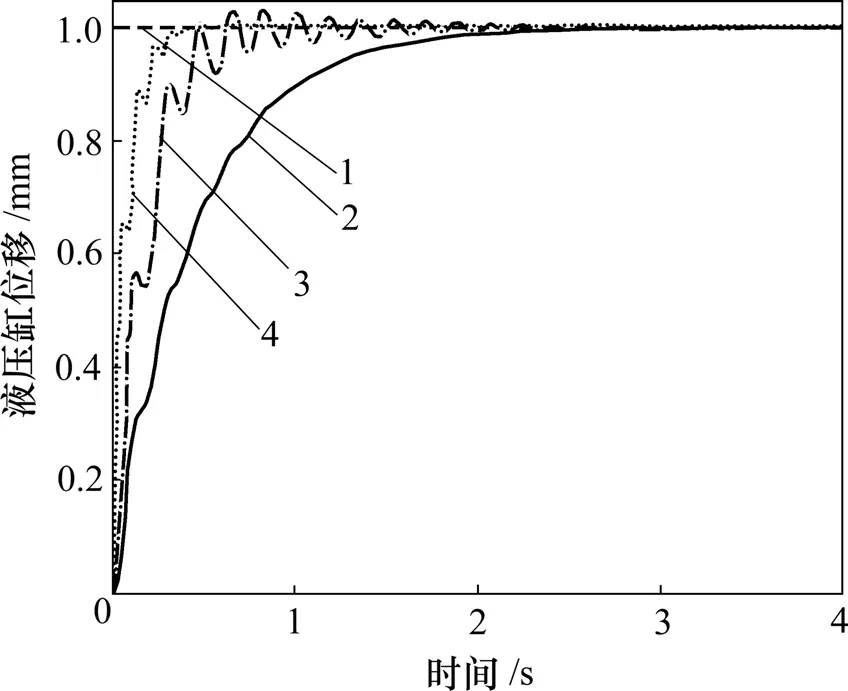
图7 单位阶跃响应对比曲线Fig.7 Comparison curves of simulation unit step response

本研究在MATLAB/SIMULINK的环境下，利用MATLAB实时视窗目标来实现系统的实时控制和信号处理，用设计的控制器直接控制电液位置伺服系统，对其进行半物理仿真试验、在线地检验系统控制[14]。输入为单位阶跃信号，仿真结果如图8所示。PID控制稳态精度高，但参数变化的适应能力较差，系统调整时间长，快速性能不好；fuzzy-PID控制器的快速性能较好，但系统存在一定得振荡；规则自校正fuzzy-PID控制器很好地抑制了系统超调，而且快速性能好，稳态精度较高。

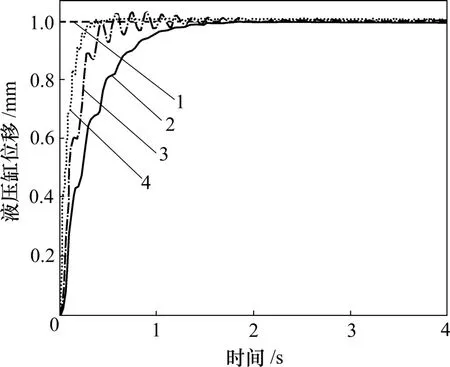
图8 半物理仿真曲线Fig.8 Curves of semi-physical simulation

分析仿真结果表明：系统实际产生的波形与计算机仿真的波形不太一致，曲线并不平滑。采用fuzzy-PID控制和规则自校正fuzzy-PID控制时，实验结果比仿真结果好，主要是因为控制器在 RTW 下的仿真实验中，引用了Look-Up Table模块，其中数据间的线性插值关系并不能完全反映模糊控制器的查表方式[15]。另外，离线数字仿真是建立在系统辨识的线性模型基础上的，而在实际系统中还有许多不确定性和非线性因素的影响。半物理仿真实验的结果和计算机仿真的结果总体上趋于一致。

5 结论

(1)对电液位置伺服系统进行了模型辨识和验证；以辨识获得的传递函数为对象设计了控制器，并用 Simulink进行了离线仿真，规则自校正fuzzy-PID控制器大大提高了系统的快速性能并使系统的稳态误差基本消除。

(2)采用规则自校正 fuzzy-PID控制器的系统的动、静态性能明显优于普通的 fuzzy-PID控制和 PID控制的动、静态性能，且对系统参数变化具有很好的鲁棒性。

[1] 王占林. 近代电气液压伺服控制[M]. 北京: 北京航空航大学出版社, 2005: 1-5.WANG Zhan-lin. Modern electricity hydraulic servo control[M].Beijing: Beijing University of Aeronautics Astronautics Press,2005: 1-5.

[2] 李洪人. 液压控制系统[M]. 北京: 国防工业出版社, 1981:4-7.LI Hong-ren. Hydraulic control system[M]. Beijing: National Defense Industry Press, 1981: 4-7.

[3] 吴博. 基于定量反馈理论的飞行模拟器运动平台控制系统研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2007: 41-45.WU Bo. Research on flight simulator motion platform control system based on quantitative feedback theory[D]. Harbin: Harbin Institute of Industry. School of Mechanical and Electrical Engineering, 2007: 41-45.

[4] 刘金琨. 先进PID控制及其Matlab仿真[M]. 北京: 电子工业出版社, 2003: 15-25.LIU Jin-kun. Advanced PID control and its Matlab emulation[M].Beijing: Electronics Industry Press, 2003: 15-25.

[5] 潘祥亮, 罗利文. 模糊 PID控制在工业锅炉控制系统中的应用[J]. 工业炉, 2004, 26(3): 38-40.PAN Xiang-liang, LUO Li-wen. Application of the Fuzzy-PID control in industrial boiler control system[J]. Industrial Furnace,2004, 26(3): 38-40.

[6] 李士勇. 模糊控制: 神经控制和智能控制论[M]. 哈尔滨: 哈尔滨工业大学出版社, 2004: 2-7.LI Shi-yong. Fuzzy control: Neural networks and intelligent control[M]. Harbin: Harbin Institute of Industry Press, 2004:2-7.

[7] 朱丽业, 吴惕华, 方园. 直接自适应模糊算法参数的选取以及仿真分析[J]. 系统仿真学报, 2006, 18(11): 3063-3067.ZHU Li-ye, WU Ti-hua, FANG Yuan. Parameters selecting of direct adaptive Fuzzy control and simulation[J]. Journal of System Simulation, 2006, 18(11): 3063-3067.

[8] HAN Gui-hua, CHEN Li-hua, SHAO Jun-peng. Study of fuzzy PID controller for industrial steam turbine governing system[C]//Proceedings of ISCIT 2005—International Symposium on Communications and Information Technologies. Beijing:Institute of Electrical and Electronics Engineers Computer Society, 2005: 1228-1232.

[9] 石贤良, 吴成富. 基于MATLAB的最小二乘法参数辨识与仿真[J]. 微处理机, 2005(6): 44-46.SHI Xian-liang, WU Cheng-fu. Rls parameter identification and emulate based on Matlab/Simulink[J]. Microprocessors, 2005(6):44-46.

[10] Ding Y S, Ying H, Shao S H. Typical Takagi-Surgeo PI and PID fuzzy controllers: Analytical structures and stability analysis[J].Information Sciences, 2003, 151: 245-262.

[11] Golea N. Indirect fuzzy adaptive model-following control for robot manipulators[C]//Proceedings of the 2002 IEEE International Conference on Control Applications. Glasgow:United Kingdom, 2002: 198-202.

[12] 顾生杰, 刘春娟. 基于模糊自整定 PID控制器的非线性系统仿真[J]. 兰州交通大学学报, 2004, 23(3): 62-64.GU Sheng-jie, LIU Chun-juan. Simulation of nonlinear-ear control system based on self-adjusting PID controller of fuzzy inference[J]. Journal of Lanzhou Jiaotong University, 2004,23(3): 62-64.

[13] 薛定宇, 陈阳泉. 基于MATLAB/Simulink的系统仿真技术应用[M]. 北京: 清华大学出版社, 2002: 404-416.XUE Ding-yu, CHEN Yang-quan. System simulink and application based on MATLAB/Simulink[M]. Beijing: Tsinghua University Press, 2002: 404-416.

[14] 张立勋, 董玉红, 王怀军. 基于半物理仿真技术的机电伺服系统模型辨识研究[J]. 机电一体化, 2006, 12(2): 30-32.ZHANG Li-xun, DONG Yu-hong, WANG Huai-jun. Research on model identification of mechatronic servo system based on hardware-in-the- loop simulation technology[J]. Mechatronics,2006, 12(2): 30-32.

[15] 邵俊鹏, 韩桂华, 董玉红, 等. 电液位置伺服系统模型辨识及其控制方法[J]. 中南大学学报: 自然科学版, 2008, 39(2):333-337.SHAO Jun-peng, HAN Gui-hua, DONG Yu-hong, et al. Model identification and control method of electro- hydraulic position servo system[J]. Journal of Central South University: Science and Technology, 2008, 39(2): 333-337.