海底钴结壳采矿车微地形导向声纳探测的圆形阵设计

王强，鄂加强

(1. 中国计量学院 质量与安全工程学院，浙江 杭州，310018；2. 湖南大学 机械与汽车工程学院，湖南 长沙，410082)

富钴结壳是大洋水下矿产资源中一种含量非常高的矿产，它以一种“壳状”沉积广布于水下海山上，呈层叠状覆盖，厚度为20～200 mm。在低纬度海域深1～3 km的水下平顶海山的斜坡上发育最好，而在平坦表面不发育[1-2]。20世纪80年代人们主要致力于钴结壳勘探，20世纪90年代则较多地探讨其开发问题。目前，钴结壳开采方法中既参考了陆地开采、海底石油开采、深海潜水器等方面的技术成果，也大量借鉴了多金属结核开采时所取得的经验。然而，迄今为止，大多数基于海底自动采矿车的开采方案都处于实验阶段。Halkyard等[3-4]对海底采矿车方案进行了研究，提出了从深海海山上开采钴结壳的采矿车设计方案及需要解决的技术问题。四轮驱动履带式海底采矿车在采集过程中如何实时控制切削深度是钴结壳开采的关键技术这一，而切削深度主要由钴结壳厚度、废石混入率和采集率确定[5]。准确获得海底微地形表面高程数据对于建立最佳切削深度分级模型至关重要。作为海底采矿车上的导航系统中的核心环节是微地形近程探测声纳，它要求尺寸小、方向到达角(DOA)分辨力强，且能在1 km水下完成工作。结合具体的钴结壳探测环境和采矿车技术要求，我国研究者在换能器布局、系统结构以及信号采集和处理等方面进行了系列研究，提出多子阵幅度-相位联合检测法，利用海底回波信号的幅度和相位信息，探测海底地形，并确定了基于能量相关搜索法和摆动式单波束的海底钴结壳微地形探测方法[6-7]。但这2种方案仍然基于线型阵列形式来发射和接收回波信号，并采用传统的波束形成算法来探测地形。实际海山表面地形复杂，难以区分底质特性和地形起伏，且线阵不具备垂直分辨力，不利于为采矿车提供实时、准确的微地形高程数据。基于声纳水平阵的优点，本文作者提出构造钴结壳微地形探测声纳圆形阵以增强水平和垂直分辨率，并在 Fourier变换的框架下提出圆阵波束形成的快速算法，以提高系统的实时性。

1 采矿车微地形导向声纳设计原理

1.1 微地形近程探测声纳

声纳是一种水下探测设备，被广泛用于海洋开发、研究海底地形、水文测量、海洋石油勘测、水下作业、探测海底礁石等领域[8]，能完成海底表面状况数据获取的主要技术有声纳成像、海底照相、电视录像和立体摄影成像等。但采矿车在采集过程中由于水的扰动会使周围海水变混浊，加上海水对光波衰减很大等，比较适合采用声纳成像技术[9]。目前，主要有多波束测深声纳系统(MBSS)和测深侧扫声纳(BSSS)系统[10]。对海底采矿车其近程导向声纳有一些要求：探测装置要求被安装在采矿车前端，并探测垂直高度在2 m以内、水平宽度在5 m以内的区域[6]。目前，根据不同用途对微地形探测的设备多为传统的超声波单波束多探头探测系统，它们是利用预定阀值比较电路来测量声波信号渡越时间进行距离计算。虽然信号处理速度快，但抗干扰能力差，尤其在恶劣的环境下，如采矿机器人颠簸、声波信号混响等因素的影响，容易出现“伪地形”[5]。

1.2 传统线阵

罗柏文等[5-6]主要采用BSSS构架，基于线阵发射和接收回波，利用差分相位法进行估计探测点。主要利用散射体回波信号角度和相邻换能器接收信号相位差来探测海底地形。尽管原理容易理解，但相位差测量会受一些因素的影响，如环境噪声、水体散射和多路径干扰等[9]。线阵是常用的阵列，对于一个N元均匀线阵，阵元间隔为d，其声学换能器波束照射范围如图1(a)所示，其中：2表示横向波束角；3表示纵向波束角。图1(b)所示为线阵传统波束形成信号处理框架，它的阵响应向量为[11]：式中：θ为入射平面波方向与阵的法线方向的夹角，为信号到达角。线阵响应向量只是θ的函数，因此，线阵只能够分辨一维信号到达角，它主要通过调整加权系数完成波束形成。阵列输出是对各阵元的接收信号向量x(n)在各阵元上分量的加权和，可表示为：

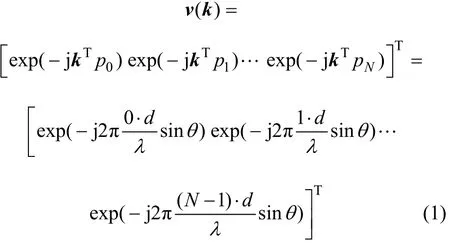
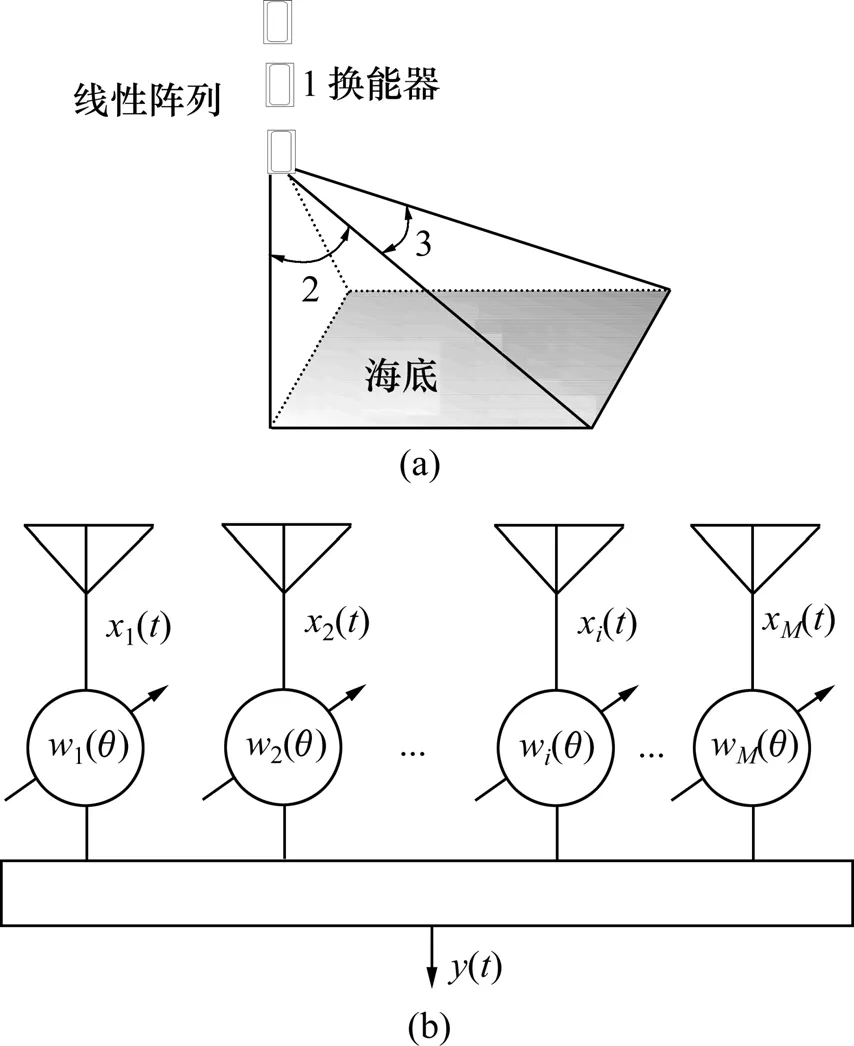
图1 超声换能器线阵与信号模型Fig.1 Schematic structure of ultrasonic transducers and linear array beamformer

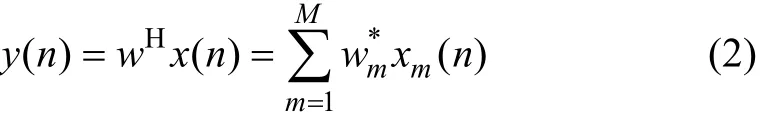
32元线阵的傅里叶波束如图 2所示。在-90°～0°范围内，不同角度上形成的波束宽度不同。越靠近旁射(0°)方向，波束越窄，分辨力越高，这也是线阵的缺点之一；线阵另外一个缺点是存在左右模糊性。因此，希望设计平面阵的傅里叶波束以估计多个信号的二维到达角。常用的平面阵有矩形阵、圆环阵与六角形阵等，它们的共同特点是都可以同时估计信号的仰角θ和方位角φ[12]。

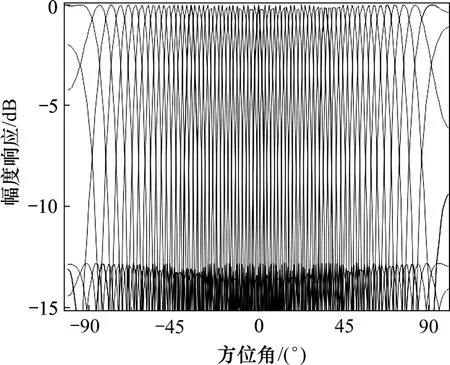
图2 32元线阵均匀间隔多个傅里叶波束Fig.2 Simulation beampattern of 32-element linear array,beam vs azimuth angle

波束形成是一种运算密集的算法，因此，在实际应用中，一个重要的问题是其运算的效率[11]。常用的解决方法是对输入信号分别进行一次时间和空间的Fourier变换。对于M个阵元和M个波数，常规波束形成和离散Fourier变换波束形成的运算量都是M2，而快速 Fourier变换波束形成可将运算量缩小为Mlog2M，且随着M的增大，两者差别就越大。具有商业开采性质的海底采矿车行走速度快，又是近程探测，因此，回波信号接收响应时间极短，数据密集。可见：采矿车对于波束形成计算速度要求较高，算法要具备良好的实时性。

目前，高分辨率波束形成技术(DOA估计)可以分辨不同方向同时到达的信号[11,13]，它在地形复杂区域能获得较好的探测性能。本研究设计平面圆阵接收声纳回波数据，在Fourier框架下利用高分辨率波束形成技术对微地形进行探测，以提高其在复杂海底对于多个凸起结壳状目标回波的DOA估计能力。

2 采矿车微地形导向声纳的圆形阵设计及其仿真

2.1 圆阵波束形成与仿真

对于1个均匀圆阵，考虑圆阵(CA)的半径为r，在圆周上均匀对称布置有M个声学换能器，如图 3所示。考虑有一平面波阵面相对接收阵的方位角θs，水平角为φs，则其波数向量k可表示为[12]：

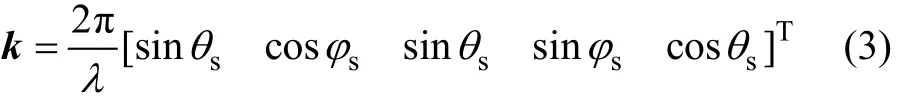
阵列的参数位置P为：

对于波束的相移为：

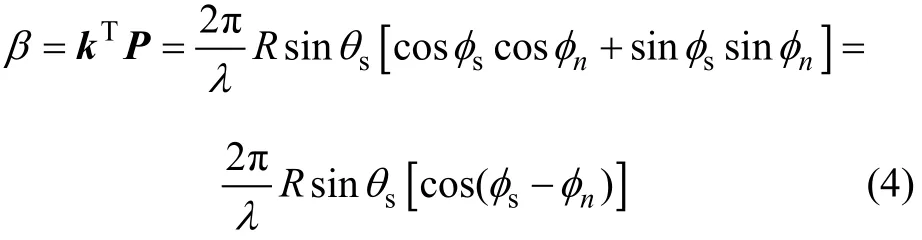
则原始发射信号s(t)在接收阵接收的信号x(φ,t)可表示为：

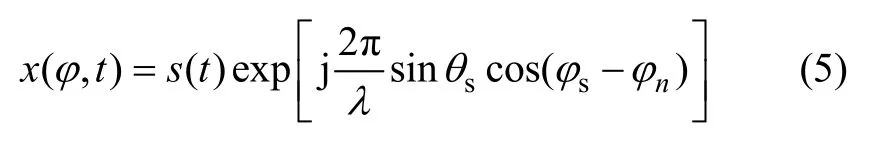
进行常规波束形成(CBF)后，输出表示为：

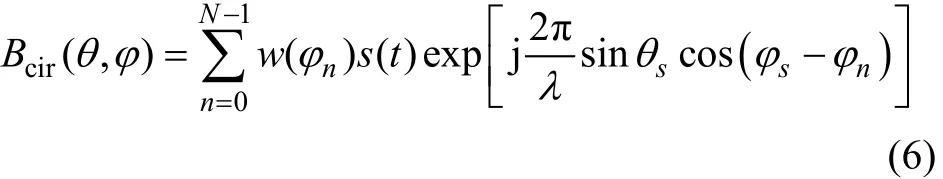
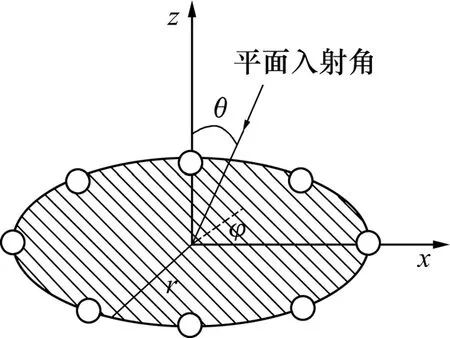
图3 圆阵几何结构与方位Fig.3 Structure and orientation of uniform circular array

图4所示为M=14阵元均匀布阵的圆阵归一化波束[14]。主瓣比旁瓣高约5.5 dB，DOA的指向性较好，有利于准确定位。圆阵的半径满足2πR/λL=10(其中，λL为频率下限时的波长)。仿真信号为18～20 kHz的线性调频信号，持续时间为0.05 s，声速为1.5 km/s。采样频率为 100 kHz，信号到达方位角(θ,φ)分别为：θ=30°,φ=64.8°。

图4 14阵元均匀布阵的圆阵波束Fig.4 Beampattern of 14-element uniform circular array

在仿真实验中，声源位置(θs,φs)假设为(200°，-30°)，均匀圆阵半径r为 0.12 m，布置14个换能器。假设目标是单频15 kHz的信号，水中声速为1.5 km/s。在图5中，主波束比旁瓣高约6 dB，可知它对于旁瓣具有较强的压抑能力，虚线圆表示目标源的位置，定位较准确。

2.2 圆阵的傅里叶波束形成

Farrier等[15]提出了圆阵波束形成的一种快速算法，圆阵的第n个阵元波束的相移为：

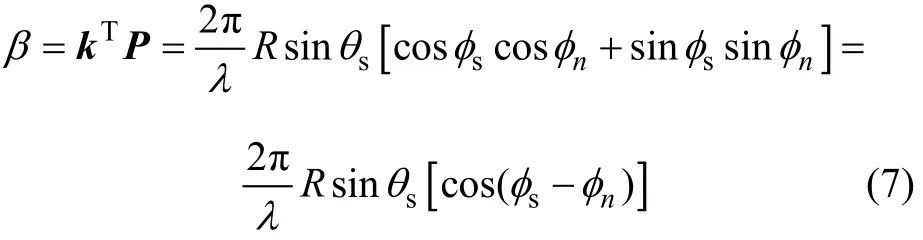
因原始发射窄带信号s，不考虑时间因子，对应接收阵接收到的信号可以表示为：

式中：k0=2π/λ；(θs,φs)为信号的入射方向。式(8)可以改写成贝塞尔函数级数形式：

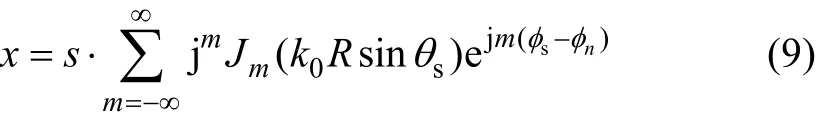
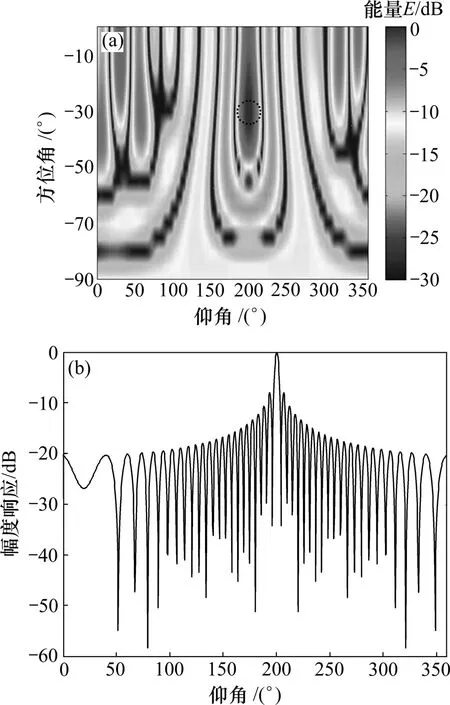
图5 均匀圆阵波束与方位角-30°时波束模式Fig.5 Simulation beampattern of beam of CA vs azimuth angle (elevation angle is -30°)

当m的阶数超过M时(其中M=2πR/λ)，可以近似为0。因此，波束形成表达式为[16]：

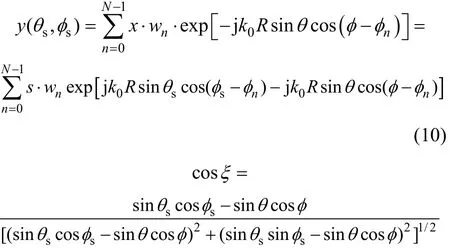
设圆阵在整个圆环上均匀分布，经归一化得到φn=2πn/N,wn=1/N，通过变换最终可以得到波束y的广义傅里叶级数形式：

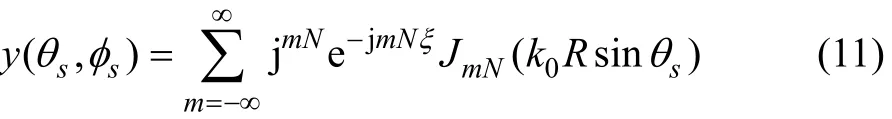
可见：可以通过式(11)得到圆阵傅里叶变换波束图。

3 实验分析

根据前述仿真分析可知：采用圆对称阵型可减少物理尺寸，具有较好的空间水平和垂直的分辨力。在360°平面内具有相等的主波束宽度和良好的指向性[11]。而波束角是换能器设计的重要参数，纵向波束角r取 1.5°～3°，横向波束角取 90°[6]。在相位激励模式条件下，圆阵对于同一平面内的角度估计可以近似看成一个虚拟的线阵，虚拟线阵的归一化波束为：

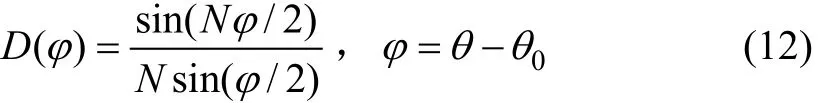
零度指向波束的3 dB宽度为：

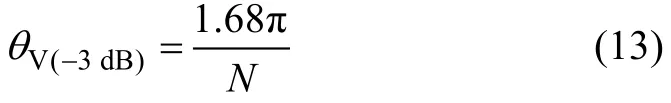
虚拟线阵在各个方向上的分辨力都是一样的，保持圆阵在各个方向均匀一致的测向能力。当真实线阵的等效孔径等于圆阵的直径时，虚拟线阵和真实线阵的波束宽度近似相等。如果圆阵半径为r，那么M=2πr/λ，此时θV(-3dB)=0.84λ/(2r)。经计算可知：需要安装 14个换能器。圆阵的半径满足 2πr/λL=10，λL=c/f=0.01 m，半径r为0.12 m，阵列是直径为24 cm的圆，均匀布置14个换能器。

在浅水区域进行模拟实验，深度为4～20 m，水底主要是沉积层物质和多个结壳型锥形物体模拟海底凸起物。声纳接收阵为圆阵，发射频率为25～50 kHz的LFM信号，脉冲宽度为4 ms。对水底噪声和回波能量进行定量分析，结果如图6所示。

从图6(a)可知：水底凸起壳状物回波的功率较强，水底形貌较复杂，呈现出多个凸形物回波强度在120～138 dB的信号；而图6(b)则反映水底噪声强度主要分布在40～60 dB之间，二者相差60～75 dB。对水底结壳凸起目标进行近程探测，图7所示为不同仰角(0°, -36°, -54°, 72°)时，水底结壳状目标回波距离和方位角之间的显示关系。由图7可知：随着仰角的增大，水底目标的回波能量不断增强，但不同的目标仍然可以根据能量的峰值来确定，0.05 m处有8个明显能量集中区域，主要是水底混响所反射的回波聚焦而成，而非目标反射回波的能量峰值，分布在0.15～0.2 m处的亮点则是多个凸形目标的形成的能量集中区。由图7(a)可见：当仰角很小时，对于距离较远处凸起结壳状物定位仍较准确，方位角为120°，距离为0.25 m。

当仰角为-36°时，方位角和距离的关系如图 7(b)所示。由图7(b)可知：在0.15 m处存在能量较强的回波，主要是混响造成的；而在0.25 m处，对于多个凸起状目标的回波仍有较强的分辨能力。从图7(c)和7(d)可知：系统能同时准确定位11处圆锥形结壳状物体，对于正方面的多个目标也有较强的DOA分辨能力。

图6 试验区域底部回波和噪声信号功率Fig.6 Echo and environmental noise power level

图7 试验区域水底多凸起结壳状目标定位Fig.7 Cone cobalt crust multi-object localization in test area

4 结论

(1)从钴结壳采矿车导向声纳换能器的布局和信号实时处理角度出发，设计了便于采矿车安装的小尺寸 14元均匀圆阵来代替传统的线阵，同时，在快速Fourier变换下提出了圆阵波束形成的快速算法，以提高DOA的分辨率和实时性。

(2)主瓣比旁瓣高约5.5 dB。所设计的14阵元圆阵有很好的指向性、垂直和水平分辨力。

(3)对于水底近程区域(5 m 以内)多目标(结壳状物体)仍具有较大的方向到达角(DOA)分辨率，在不同的仰角(0°, -36°, -54°, 72°)下对 11 处模拟钴结壳凸起物可实现准确定位，定位精度可达到0.04 m，有助于提高微地形的探测精度。

[1] 孙春宝, 吕继有, 李浩然. 大洋多金属锰结核酸浸贵液中铁锰元素的脱除[J]. 中国有色金属学报, 2006, 16(3): 542-548.SUN Chun-bao, LÜ Ji-you, LI Hao-ran. Removal of iron and manganese element from ocean multimetallic nodules acid leaching solution[J]. The Chinese Journal of Nonferrous Metals,2006, 16(3): 542-548.

[2] 罗春雷, 胡均平, 刘伟. 钴结壳开采装置及方法[J]. 中南工业大学学报: 自然科学版, 2002, 33(6): 617-620.LUO Chun-lei, HU Jun-ping, LIU Wei. Seabed cobalt shell exploiting equipment and method[J]. Journal of Central South University of Technology: Natural Science, 2002, 33(6):617-620.

[3] Halkyard J E. Technology for mining cobalt rich manganese crusts from seamounts[C]//Proceedings of Oceans’85. New York : IEEE Publisher, 1985: 352-374.

[4] Chung J S. Deep-ocean mining: Technologies for manganese nodules and crusts[J]. International Journal of Offshore and Polar Engineering, 1996, 6(4): 244-254.

[5] 罗柏文, 周知进, 史春雪. 基于幅度特征相关性的海底微地形探测方法研究[J]. 矿业研究与开发, 2006, 26(4): 51-54.LUO Bo-wen, ZHOU Zhi-jin, SHI Chun-xue. Study on exploration method of seabed tiny terrain based on the relativity of amplitude characteristics[J]. Mining Research andDevelopment, 2006, 26(4): 51-54.

[6] 罗柏文, 卜英勇, 周知进. 基于能量相关搜索法的海底钴结壳微地形探测方法研究[J]. 矿冶工程, 2007, 27(1): 21-24.LUO Bo-wen, BU Ying-yong, ZHOU Zhi-jin. Exploration method for tiny terrain of seabed cobalt crust based on energy relativity search[J]. Mining and Metallurgical Engineering, 2007,27(1): 21-24.

[7] 赵海鸣, 卜英勇, 王纪婵, 等. 摆动式单波束超声波水下微地形探测[J]. 中南大学学报: 自然科学版, 2007, 38(5):932-936.ZHAO Hai-ming, BU Ying-yong, WANG Ji-chan, et al.Detection of seabed cobalt-rich crusts micro-topography based on single-beam ultrasonic wave[J]. Journal of Central South University: Science and Technology, 2007, 38(5): 932-936.

[8] 朱维庆, 朱敏, 刘晓东. 海底微地貌测量系统[J]. 海洋测绘,2003, 23(3): 27-31.ZHU Wei-qing, ZHU Min, LIU Xiao-dong. The survey system for detailed relief on sea floor[J]. Hydrographic Surveying and Charting, 2003, 23(3): 27-31.

[9] Jin G L, Tang D J. Uncertainties of differential phase estimation associated with interferometric sonars[J]. IEEE Journal of Oceanic Engineering, 1996, 21(1): 53-63.

[10] 李启虎. 数字式声纳设计原理[M]. 合肥: 安徽教育出版社,2003: 420-461.LI Qi-hu. Digital sonar design principle[M]. Hefei: Anhui Education Press, 2003: 420-461.

[11] van Trees H L. Optimum array processing[M]. New York: John Wiley & Sons, 2002: 284-289.

[12] Naidu P S. Sensor array signal processing[M]. Boca Raton: CRC Press, 2001: 110-117.

[13] Xu W, Stewart W K. Coherent source direction estimation for three-row bathymetric sidescan sonars[C]//Proceedings of Oceans’99. New York : IEEE Publisher, 1999: 299-344.

[14] 陈丰. Fourier 变换在平面、柱、球阵波束形成和DOA估计中的应用[D] . 杭州 : 浙江大学信息与电子工程系, 2006 :31-36.CHEN Feng. FFT implementation in planar, cylindrical and spherical array processing and DOA estimation[D]. Hangzhou:Zhejiang University. Department of Information Science and Electronic Engineering, 2006: 31-36.

[15] Farrier D R, Nightingale J M. Fast beamforming techniques for circular arrays[J]. Journal of the Acoustical Society of America,1975, 58(4): 920-922.

[16] Ioannides P, Balanis C A. Uniform circular and rectangular arrays for adaptive beamforming applications[J]. IEEE Antennas and Wireless Propagation Letters,2005, 4(3): 351-354.