椭圆范围矩形相关点的一个结论及应用*
2020-05-13 13:50广东省惠州市实验中学516003肖志向
中学数学研究(江西) 2020年3期
广东省惠州市实验中学 (516003) 肖志向
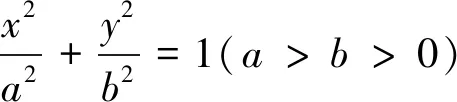
先证明点A为(a,-b),点B(0,b)时的结论成立.
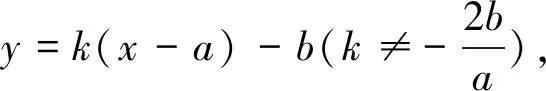
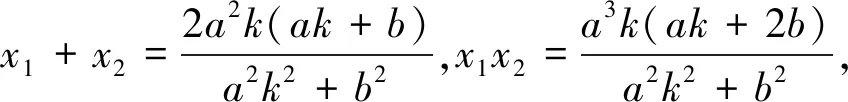

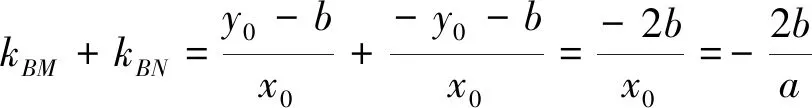

设M(x1,y1),N(x2,y2),则有x1+x2
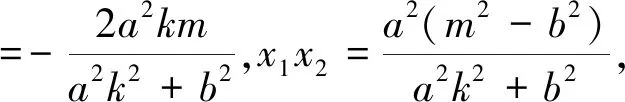
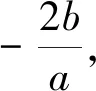
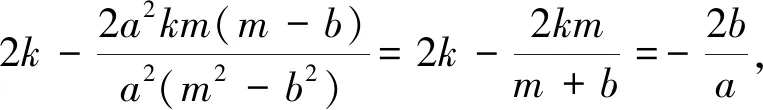
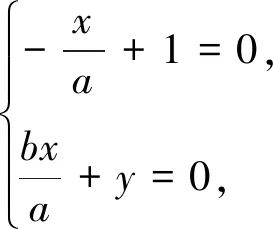
综合以上可知,三点A、M、N共线的充要条件是kBM+kBN=kAB.
其他三种情形,即点A,B的坐标分别为点
A(-a,-b),点B(0,b);A(a,b),点B(0,-b);A(-a,b),点B(0,-b)时,类似以上过程,容易得到相同的结果,故结论是成立的.(请读者自行检验)


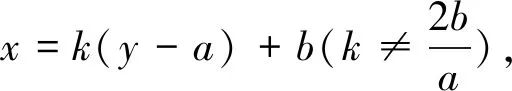
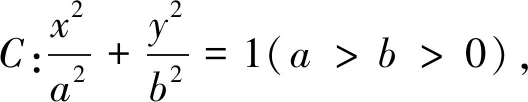
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.

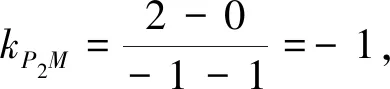
猜你喜欢
新高考·高一数学(2022年3期)2022-04-28
中学政史地(2021年31期)2021-12-09
中学数学研究(江西)(2021年9期)2021-10-22
中等数学(2021年4期)2021-08-14
高中生·天天向上(2018年7期)2018-07-23
小天使·一年级语数英综合(2016年5期)2016-05-14
红领巾·萌芽(2016年3期)2016-04-28
体育师友(2013年6期)2013-03-11

