对数是个万花筒
——以同一份试卷中的一类题为例
江苏省苏州市田家炳实验高级中学 (215004) 周 磊
笔者最近给学生布置了一份本地上一届高三期中数学联考的试卷,经过仔细的研究和思考,笔者发现了一个有趣的现象,整份试卷中,填空题的压轴题、解答题的压轴题以及附加题的压轴题不约而同地都涉及到了函数y=lnx的几个不等关系,都与函数y=lnx的图象有关.受此启发,笔者将以这份试卷中的这三个压轴题来谈一下高三解题教学中,如何进行从“有解”到“优解”的教学实践,与同行交流.
1.试题呈现

问题2 (苏州市五市四区高三(上)期中第19题)已知函数f(x)=lnx,g(x)=x2-x-m.
(2)若m=0,求函数F(x)=f(x)-g(x)在(0,a]上的最大值;
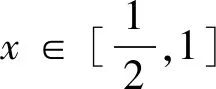
问题3 (苏州市五市四区高三(上)期中第23题)(1)若不等式(x+1)ln(x+1)≥ax对任意x∈[0,+∞)恒成立,求实数a的取值范围;

2.背景初探
结合笔者教学实践,不难发现这三道压轴题都涉及常见的指数或对数函数不等式,具体如下:

不等式2 lnx≤x-1,当且仅当x=1时取等.
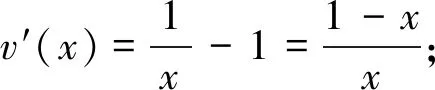
不等式2-1ex≥ex,当且仅当x=1时取等.
证明:由不等式lnx≤x-1可知elnx≤ex-1,即ex≥ex.
不等式2-2ex≥x+1,当且仅当x=0时取等.
证明:在不等式lnx≤x-1中,用ex代替x,即lnex≤ex-1,有ex≥x+1.
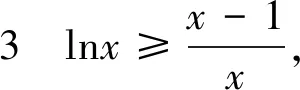
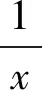

不等式4 lnx≤x(x-1),当且仅当x=1时取等.


图1
评注1:上面的几个函数不等式,本质上也可以用函数图象来表达,如图1,即函数y=lnx与几个初等函数的图象关系,通过“数”的证明和“形”的说明,可以很好地扩充学生的审题视野,丰富学生的解题视角.
3.问题再析
下面,利用上述函数不等式对这几道压轴问题进行分析,首先是“有解”,即运用通性通法顺利解决问题;再去研究是否有别的途径进行“多解”探究,最后才有可能达到“优解”的阶段.

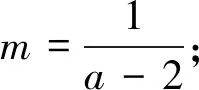

针对填空题,问题1的解答利用图形特征,这里需要说明的是,如果这是解答题,还是要通过零点判定定理去证明,这种方法也被众多高三师生所熟悉和使用,以问题2的通解为例:
问题2通解:由f(x)+g(x) =-3,即当m≥-3时,原函数不等式成立. 不可否认,这种解法思路分明,思维严谨,但是在追求最优解的解题道路上,能否再思考的深入点呢?问题中同时出现了ex和lnx,由前文几个不等关系可知,这两个函数都可以与多项式函数有联系,为此,不妨采用这个思路去分析,过程如下: 问题3证明(1)设函数f(x)=(x+1)ln(x+1)-ax,其中x∈[0,+∞),有f′(x)=1-a+ln(x+1). 当a≤1时,f′(x)≥0,fmin(x)=f(0)=0,则a≤1满足题意; 综上可知a≤1. 当a>1时,当h′(x)≥0时,x≥a-1;当h′(x)≤0时,0≤x≤a-1;有hmin(x)=h(a-1)=lna-(a-1)<0,因此a>1不合题意.” (3)若第(1)题是填空题的话,也可从几个角度进行分析: 视角1 当x=0时,a∈R; 视角2 设t=x+1(t≥1),即tlnt≥a(t-1)恒成立,其中u(t)=tlnt在[1,+∞)为单调递增函数,且过点(1,0),直线y=a(t-1)始终在函数u(t)=tlnt的图象下方,则a≤u′(1)=1. 视角3 设t=x+1(t≥1),即tlnt≥a(t-1)恒成立,其中u(t)=tlnt; 当t=1时,a∈R; 本文中,通过对一张期中联考试卷中的三个函数压轴题进行仔细分析,结合笔者自身的教学实践,也触发了一些思考和感悟: 感悟1:从联系的视角理解数学 数学解题教学是数学教学工作中的一项艰巨而重要的任务,尤其是面对像高考这种选拔性的考试,高考试题的命制理念之一就是试题源于教材,又要高于课本.高三一轮的复习过程中,特别要关注教材,以教材为蓝本帮助学生数学建好知识联系的框架,帮助学生更好地理解数学.文中研究的这几道以函数与导数为背景的压轴题,对学生理解数学有着极好的引导作用.具体而言,理解数学要“把书读薄”,即要明白知识的核心和本质是什么,不同知识结构之间的联系,对教材内容的结构发展有着深刻的认识,充分明白数学教材中关键知识点之间的相互转化过程.这样的解题教学才是高效的,作为求知者的学生才能从被动的解题中解放出来,知晓知识的来龙去脉,深究核心知识的数学本质,从而做到了然于心,方能运用自如. 感悟2:用创新的思维研究数学 数学问题总是千变万化,解一题并通一类,是数学解题的终极目标.作为教者,首先要更新观念,多学习,多思考、多准备,充分做到备教材、备学生、备教法.具体而言,要想提升解题教学的效果,首先,教师应善于研究学生的思考方式值得仔细研究,它既是学生学习和解决问题的核心要素.本文研究所分析的这类问题,一方面可以沿着学生的思路引导学生展开思考,让学生厘清解题思维的切入点、转折点和关键点,探究通法并解决问题;另一方面,也可以通过评析问题并解释清楚其中的问题内涵,发掘一类问题的本质属性,另辟蹊径,从而可用创新的思维去研究数学问题,实现从“有解”到“优解”的解题境界,促进师生共同提升思维品质.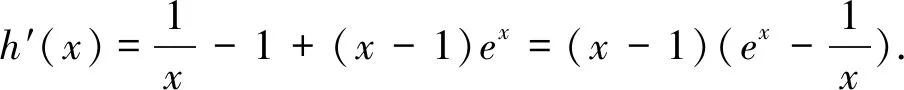

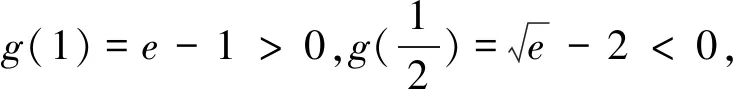
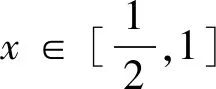
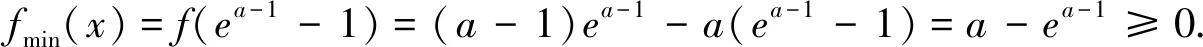
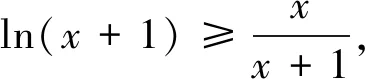

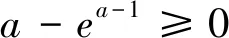


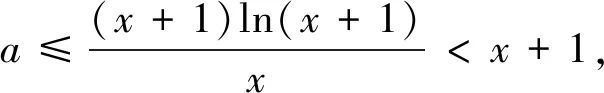

4.解题感悟

