多差速驱动重载AGV运动学建模及运动控制

金小琳 顾文昊 冯 迪 李俊明 须晓峰

（上海沃迪智能装备股份有限公司，上海，201506）

0 引言

随着工业机器人行业的飞速发展，为实现高效、有序的智能化工厂车间，AGV凭借其高效、智能、安全的特性，在仓储、物流运输中得到了极大的应用。

轮式全方位移动机器人驱动系统常采用万向轮[1]、麦克纳姆轮[2-3]、正交轮[4]、球轮[5]等。但这类轮子在承载重载方面的能力相对较差，因此常用于负载5t以下的物体。全方位移动机器人以其运动的灵活性和稳定性，常应用于电商等行业的分拣、物流工作中。

舵轮常应用于重载AGV结构中，通常采用单驱、双驱舵轮[6-7]结构、使用驱动轮带动承重轮的方案，但这样的结构无法使AGV车体达到全方位的移动能力。因此，在轻载AGV与大型重载AGV之间的20t级全方位移动AGV成为了产品空白。

Kim等人[8]提出一种四轮独立方向盘配置的舵轮驱动全方位移动AGV，并对其进行运动学建模，这后来成为四轮驱动全方位移动机器人常用的建模方法。武星等人[9]在其基础上提出了一种基于leader-follower的控制策略。

本文提出的多差速驱动重载AGV结构，通过使用多个差速单元协同控制，所有的轮均为驱动舵轮，为重载AGV提供了更大的驱动力；通过脚轮单元的差速转向，可以满足重载AGV的全方位移动。

本文采用刚体力学原理，对多差速驱动重载AGV进行运动学建模，在增广坐标系下求得其运动学模型，得出运动学逆解公式；讨论全方位重载AGV几种特殊的运动方式，验证其为全方位移动机器人；提出针对多差速驱动结构的轨迹规划方案；结合多差速驱动重载AGV的模型结构，提出内环-外环串联的PID控制模型策略，内环分别对驱动舵轮的速度、脚轮单元的偏转角度进行反馈，外环针对重载AGV车体的运动进行闭环反馈，在保证重载AGV的运动符合预期轨迹的同时，保障其运动的平稳性；最后，在MatLab软件平台下进行模拟仿真，验证本文控制策略的有效性。

1 重载AGV运动学模型建立及分析

本文的研究对象为多差速驱动重载AGV，其结构模型如图1所示。其机械结构主要由脚轮单元、AGV车体两部分组成。其中，每个脚轮单元内包含2个驱动舵轮，平行置于脚轮单元两侧并分别由不同的驱动装置控制，且安装于AGV车架上的脚轮单元可通过2个驱动舵轮形成差速的方式，使其绕安装中心轴即单元回转中心进行转动，进而可以实现重载AGV的全方位运动。

图1 多差速驱动重载AGV的结构模型

在进行运动学建模时，首先做出如下假设：

1）假设重载AGV是一个刚性的结构，即其4个脚轮单元相对于AGV车架几何中心的位置以及脚轮单元内驱动舵轮相对于单元回转中心的位置在运动过程中不会发生变化；

2）假设运动平面平整，8个驱动舵轮均与地面接触且8个舵轮均匀分担载荷，与地面没有相对滑动，只做纯滚动运动；

3） 假设舵轮与地面径向摩擦小，不会影响舵轮轮组的转向。

将全局坐标系即地图坐标系设为二维笛卡尔坐标系XOY，在多差速驱动重载AGV车体上建立一个随其移动的AGV局部坐标系，原点位于AGV车体中心处，轴方向为AGV直行行驶的正方向，且脚轮单元对称分布于坐标轴两侧。重载AGV在地图坐标系中的位姿如图2所示，则其位置姿态可以由表示，其中表示AGV局部坐标系与全局坐标系的偏转角度，逆时针为正。由此可得，全局坐标系转换为AGV局部坐标系的转换矩阵为：

脚轮单元由脚轮架及2个平行安装的驱动舵轮组成，脚轮单元相对于AGV车体的单元回转中心位于2个驱动舵轮连接轴的中心处。重载AGV在局部坐标系中车体速度结合AGV的机械结构，可以在AGV局部坐标系中得出各个脚轮单元的单元回转中心位置坐标，其中，表示第个脚轮单元。

根据刚体运动学公式，可得出重载AGV中第 个脚轮单元在AGV局部坐标系下的速度表达式：

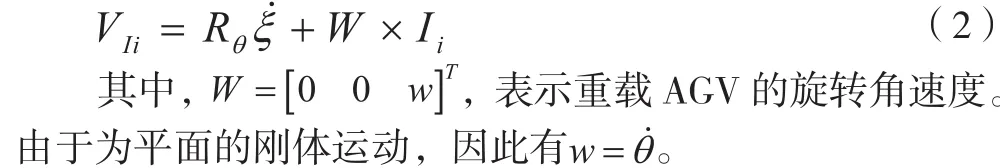
图2 多差速驱动重载AGV在地图中的位置

脚轮单元由一对平行安装的差速驱动舵轮组成，可知驱动舵轮相对于地面做纯滚动运动。因此脚轮单元受到运动学约束：沿脚轮单元局部坐标系轴方向，运动速度恒为0。即可得到左驱动舵轮、右驱动舵轮的速度关系表达式为：

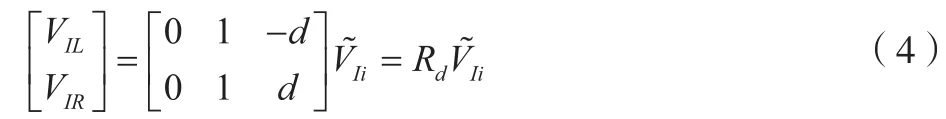
综上所述，联立公式（1）-（4）可以得出AGV车体的运动速度与驱动舵轮速度之间关系式，即运动学逆解的函数关系：

图3 脚轮单元局部坐标系

2 重载AGV几种特殊的运动方式

由于多差速驱动重载AGV中所有的轮子均为驱动舵轮，且从机械结构上脚轮单元可绕单元回转中心进行左右自由偏转，因此重载AGV能够实现全方位的运动。各个脚轮单元中驱动舵轮与AGV车体速度之间函数关系如公式（5）所示，因而对输入的AGV车体速度进行设定即可实现不同的运动方式。

图4 AGV几种特殊运动方式

下文讨论图4所示AGV的几种特殊的运动方式：半八字转弯（行驶模式）、八字转弯、斜行、横行、原地回转。

根据重载AGV的实际操作习惯，当车体进行转弯行驶、斜行行驶时，通常以行进方向最前排转弯半径最小的脚轮单元偏转角度为基准。因此对于行驶模式、八字转弯、斜行模式输入基准角度及最大舵轮行驶速度则可以对运动进行表述；对于横行模式、原地回转模式则输入最大舵轮行驶速度即可以对运动进行表述。为表述方便，设基准的脚轮单元回转中心到AGV局部坐标系轴，轴的距离分别为；驱动舵轮到单元回转中心之间的距离为；驱动舵轮的半径为。

1）行驶模式输入指令为：

AGV在行驶模式进行转弯时，其转动圆心位于车体行进方向最后侧的脚轮单元中心线上，且位于车体的外侧，与直行搭配使用，该模式直观来看与普通汽车的行驶模式相类似。

2）八字转弯输入指令为：

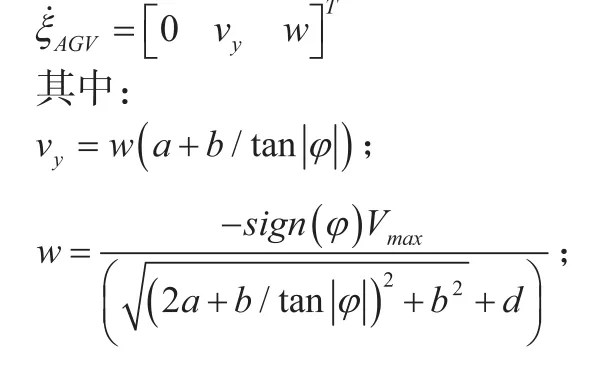
AGV进行八字转向运动时，其转动圆心位于AGV局部坐标系轴上，且位于车体的外侧，与直行搭配是常用的转向模式，其最小转弯半径比行驶模式小。

3）斜行模式输入指令为：

所有脚轮单元与AGV局部坐标系即车体运动正方向具有相同的夹角，车身方向保持不变，车体沿夹角方向运动。

4）横行模式输入指令为：

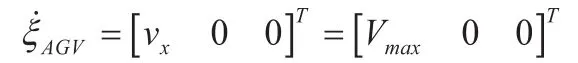
5）原地回转输入指令为：

通过运动学逆解可以求得各个脚轮单元的偏转角度及各个舵轮的转动速度，将脚轮单元进行适当方向及角度的偏转，之后使舵轮以合适的速度进行运动。此时重载AGV旋转中心位于车体的内部。

综上所述，当给AGV输入适当的指令时，车体能够进行不同模式的运动；当AGV脚轮单元在适当的偏转角度及行驶速度时，可以完成横行、原地回转等运动，因此本文研究对象多差速驱动重载AGV为全方位移动机器人。

3 重载AGV的轨迹规划

当上位机或遥控器手柄传递命令信号给重载AGV时，一般输入为速度信号。在将速度指令下发到电机之前，需要对输入的速度进行轨迹规划。为保证重载AGV安全、平稳地行驶，轨迹规划要求确保加速度的连续。结合重载AGV的结构，轨迹规划主要存在两个问题：重载AGV在行驶过程中要求加速度连续；当重载AGV起步时需要原地进行脚轮单元偏转。

第一种情况发生在：当重载AGV接收到突变（加速度不连续或者加速度过大）的速度信号时，即无法直接将接收到的AGV速度信号通过运动学逆解直接发送给驱动器和电机。针对这一情况，本文采用输入初始加速度的梯形规划对接受到的速度信号进行轨迹规划，从而得到加速度连续的速度轨迹。

在多差速驱动重载AGV结构中，脚轮单元能够左右自由偏转且具有正方向。因此，当运动模式进行切换时，以及重载AGV每次从静止状态开始运动时，需要先对脚轮单元的实际偏转角度和期望值进行对比。若偏差值较大，则需要AGV在原地转动脚轮单元偏转至合适的角度。本文采用S形规划对脚轮单元的偏转角度进行规划，来保证重载AGV的脚轮单元能够较为平稳地进行偏转。

综上所述，本文针对多差速驱动重载AGV设计的轨迹规划采用梯形规划与S形规划相结合的方式，分别针对起步时、重载AGV运行时进行规划。其流程图如图5所示。

图5 重载AGV轨迹规划流程图

4 重载AGV的运动控制模型

本文所研究的多差速驱动重载AGV结构为多差速脚轮单元协同控制结构，因此与其他轮式全方位移动机器人相比，更容易受到实际装配及环境因素影响。区别于电机直接实现脚轮单元偏转，以差速结构实现脚轮单元自由偏转的方式，使得单元偏转角度易受到地面平整度、回转中心相对于驱动舵轮的安装位置、舵轮长期磨损形成的半径不匀以及左右舵轮的大小轮等情况的影响。其中地面平整度及舵轮尺寸为不可控因素，且无法完全消除。当驱动单元偏转角度产生偏差时，重载AGV在行驶过程中会产生较大的内应力，大大减小车体的使用寿命且会造成安全隐患。因此对4个驱动单元的偏转角度进行PID控制是有必要的。

针对多差速驱动重载AGV结构，本文设计了一种内环-外环串联的PID控制策略，如图6所示。

控制模型的内环为驱动舵轮转速的反馈，其中包含驱动舵轮对应电机转速的PI反馈和脚轮单元偏转角度的PD反馈，采用、加权的方式将这两部分结合起来。如图6所示，分别表示实际AGV车体速度与理论速度偏差、驱动电机实际转速与理论转速偏差、4个脚轮单元的实际偏转角度与理论偏转角度的偏差。驱动舵轮的速度反馈的表达式为：

控制模型的外环为针对重载AGV的实际行驶速度进行的PID反馈。重载AGV车体速度反馈的表达式为：

图6 重载AGV运动控制内环-外环串联器

5 MatLab模拟仿真

本文以图2所示的4个脚轮单元、8个驱动舵轮的重载AGV结构为例进行仿真。脚轮单元在AGV局部坐标系下的位置坐标及重载AGV的机械参数分别为：

本文引入驱动舵轮转速误差、驱动轮半径误差来模拟大小轮工况及不平整地面工况给车体运动带来的影响，并通过试凑法确定

在图7中，在重载AGV运动学轨迹仿真中加入针对驱动轮的扰动后，脚轮单元的偏转角度与规划的偏转角度会产生一定的偏差，从而通过车体结构的内部协调使得重载AGV的车体运动路线产生偏离。当加入偏差后，AGV的最大轨迹偏差为：加入内环-外环串联控制后，AGV最大轨迹偏差为：

从仿真实验可知，通过加入上述的内环-外环串联控制模型进行闭环反馈控制，可以有效地对脚轮单元的偏转进行控制，从而达到控制车体整体运动偏移的目的。

图7 重载AGV运动控制仿真轨迹

综上所述，本文针对多差速驱动重载AGV结构设计的内环-外环PID控制器能够有效地进行运动控制，并可以将其应用于实际。

6 总结

本文首先介绍了一种多差速驱动全方位重载AGV，并且针对其结构进行运动学建模，从而得到通用的运动学逆解公式；其次通过对几种特殊运动模式的讨论，验证其为全方位移动重载AGV；接着使用本文提出的轨迹规划方法实现了重载AGV加速度连续、平稳地运动；然后在运动学模型基础上，提出了针对多差速驱动的内环-外环串联控制策略；最后利用MatLab仿真平台对运动学正逆解算法和PID反馈控制效果进行验证，结果表明，内环-外环串联的控制策略能够有效地控制环境带来的影响。