港机大型构件机器人打磨路径规划

方 伟 薛龙 黄继强 黄军芬 曹莹瑜 曹楷顺

（1北京石油化工学院机械工程学院，北京，102617; 2北京化工大学机电工程学院，北京，100029）

0 引言

港机装备作为现代港口作业中的核心装备，其中的门座式起重机和岸桥等均由箱梁、桁架等典型大型构件组成。由于这些大型构件是由大尺寸的钢构件拼装焊接而成[1]，故存在很多焊缝，因此，产品在制造过程中，考虑焊缝质量和外观质量的相关要求，需要对焊缝的部分区域进行打磨，才能够进入到下一道工序。目前我国港机企业在打磨工序上还主要依靠人工完成作业，存在效率低下、质量无法保证、作业环境恶劣等问题。因此，开展大型构件机器人打磨相关技术研究具有重要的现实意义。

大型构件的机器人打磨作业存在两大难题：因构件焊缝打磨点多和打磨点不确定而带来机器人打磨任务分配、路径执行顺序规划问题；大型构件多机器人打磨作业容易发生碰撞问题。为此，本文基于机器人操作系统ROS（Robot Operating System）[2-4]以及MatLab工具对港机大型构件机器人打磨路径规划中的打磨点任务分配和排序、机器人避障等问题展开研究，为机器人打磨的推广应用提供技术支撑。

1 港机大型构件打磨系统

港机构件尺寸大、结构复杂，同时在港机大型构件上存在的焊缝数量多，单台机器人打磨无法满足生产效率的需求。为此，本文设计了一套港机大型构件机器人打磨系统，如图1所示。该系统包括2台打磨机器人、搭载机器人的C型架以及与之相配的C型架导轨，其中，打磨机器人和C型架均可协同作业。

图 1 港机大型构件机器人打磨系统组成

2 机器人打磨点排序规划

本文以典型构件前大梁为例，其尺寸为74.2m×6.2m×8.5m，在焊接工序完成后存在多个打磨点，且因为焊接工艺的原因，每件构件焊接完成后的打磨点存在不确定性。机器人在进行焊缝打磨时有多条运动路径，而运动路径的执行顺序与机器人打磨的效率密切相关，采用人工示教方法会导致示教工作量非常大，费时费力，无法满足实际工作需求。所以，对机器人打磨点进行任务分配及排序规划的优劣对机器人打磨工序会产生直接影响，港机大型构件机器人打磨点排序规划算法流程如图2所示。

2.1 打磨点任务分配

港机大型构件机器人打磨系统集成2台打磨机器人执行打磨工序，针对这种多机器人协同作业模式，首先要解决的问题是任务分配，即将打磨点合理地分配给机器人。

在不考虑机器人碰撞的前提下，本文采用K-means聚类算法[5]解决多机器人打磨点分配问题。该算法将给定的数据集即打磨点的三维坐标位置信息根据和初始化的两个质心之间的最短欧氏距离分成两类，该质心代表两台打磨机器人。K-means聚类算法的流程，见图2中的多机器人任务分配部分。

2.2 打磨点排序算法

将港机大型构件打磨点任务分配给单个机器人后，需要解决单台机器人打磨点的排序问题。因考虑到使机器人完成多个打磨点作业时以总体路径最短为优化目标，所以机器人打磨点排序问题可以抽象为旅行商(TSP，Traveling Salesman Problem)问题[6-7]，即寻求单一旅行者以最短路径游览完n个城市，同时每个城市只能通过一次，最后回到出发点。

针对机器人打磨点的排序问题，可以表述为：将机器人视为旅行商，给定旅行商所要旅行点的坐标信息，即打磨点三维位置信息，其中为打磨点，代表打磨点的坐标。一条打磨路线数为条路径段组成，机器人从给定的起点出发打磨完所分配的打磨点后回到起始点，整个路径要求最短。即要求目标函数 函数值最小，由式（1）表示为：

2.3 算法寻优求解

TSP问题一般采用智能寻优算法来求解，通常选择粒子群算法。标准粒子群算法是一种基于群智能的演化计算方法[8-10]。其原理为：假设存在一个D维的空间，随机的初始化一个大小为N的种群和每个粒子的初始速度。粒子速度与位置根据式(3)、(4)更新而获得：

标准的粒子群算法虽然操作简单，但是随着迭代次数的不断增加，在种群收敛集中的同时，各粒子越来越相似，在局部最优解周边无法跳出，同时，采用随机初始化种群的方法所产生的初始粒子的适应值差异性比较大，进而导致算法的进化效率和收敛速度降低。

为了避免标准的粒子群算法自身的弊端，本文提出改进的粒子群算法——TSP-混合PSO算法（见图2多机器人打磨点排序）。该算法利用贪心算法进行种群初始化来得到较优的初始解，同时引入了遗传算法中的交叉和变异操作，摒弃了传统粒子群算法中通过跟踪极值来更新粒子位置的方法。使用粒子同个体极值和群体极值的交叉以及粒子自身变异的方式来搜索最优解，能够有效地避免标准粒子群算法在寻优过程中的弊端。

1）改进种群初始化方法。

采用贪心算法对粒子种群初始化，不考虑整体最优，从问题的初步解一步一步进行且只考虑当前最优。在将港机大型构件打磨点进行排序时，假设粒子种群大小为N，贪心算法初始化种群的过程如下：

第一步：选择机器人打磨起点加入最终最优打磨序列，并在原始种群中删除该打磨点；

第二步：计算原始种群中未加到最优打磨序列的打磨点到打磨起点最短距离的打磨点，然后添加入到最优打磨序列，并在原始种群中删除该打磨点；

第三步：重复第二步，直到将原始种群中所有的打磨点依次加入到最优打磨序列中，得到一组经优化的粒子个体；

第四步：根据粒子种群规模N重复上述步骤第一步、第二步、第三步，最终得到一组大小为NN的经优化的初始种群。

2）引入遗传算法中的交叉和变异操作。

交叉操作是指采用整数交叉法，随机选择交叉位置3和5（如图3所示），将个体和个体极值或个体极值与群体极值进行交叉得到新个体。

图3 交叉操作示意图

交叉操作后产生的新个体假如存在位置一致的情况要进行调整，其方法为用新个体中没有出现的原始打磨点来替代重复出现的打磨点（如图4所示），同时采用保存优秀个体的策略，即用新旧粒子的适应度值来评价是否更新粒子。

图4 调整操作示意图

变异操作是指采用互换个体内部两位的方法，随机选择变异位置2和4，变异结果如图5所示, 同时采用保存优秀个体的策略，即用新旧粒子的适应度值来评价是否更新粒子。

图5 变异操作示意图

基于本文所提出的TSP-混合PSO算法的解算，得到机器人打磨点排序结果，具体见后面的仿真结果。

3 机器人避障规划

3.1 机器人打磨障碍工况分析

机器人对大型构件进行打磨时，存在两种障碍工况。

一是，打磨工件主要由箱梁和桁架构成，当打磨点A和打磨点B位于横梁两侧（如图6所示）时，横梁和桁架将被视为障碍物，机器人需跨过障碍物完成打磨工作，因而必须对机器人进行避障规划。

图 6 打磨工件障碍示意图

二是，为使机器人打磨作业覆盖整个大型构件，打磨系统采用双机器人协同作业，这种多机器人协同打磨模式会产生工作路径交叉的情况，该情况下机器人之间互相视对方为障碍物，因而需要做避障规划，如图7所示。

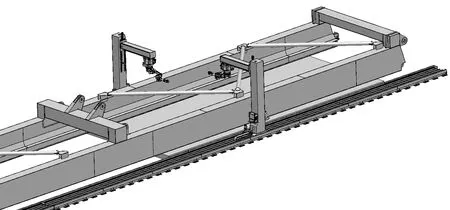
图 7 双机器人协同打磨障碍示意图

3.2 机器人避障规划算法

机器人在对港机大型构件打磨作业时，采用的模型是C型架导轨搭载两台打磨机器人，单套装置共有8个自由度。对于这种多自由度机器人的避障规划问题，本文选择RRT*算法来解决。RRT*算法既继承了RRT(Rapidly Exploring Random Tree)算法[11]的优点，同时还保证了路径的相对次优。

RRT*算法[12]使用随机节点生成路径，通过在新的节点附近建立周围节点集合来比较路径代价的方式去改进现存的搜索树，即遍历这些周围节点以检查是否存在一段更优路径，如果存在，则用这条更优路径去替换现有的最短路径。RRT*算法的基本流程如图8所示。

图 8 RRT＊算法流程图

通过RRT*算法可以快速地得到港机大型构件机器人打磨最短的无碰撞路径，具体见下节的结果。

4 路径规划仿真

4.1 打磨点任务分配算法仿真

本文利用MatLab软件，结合K-means聚类算法对多机器人任务分配进行仿真验证。从实际焊接工件中随机提取50个打磨点的三维位置信息（x,y,z），如图9所示。经过K-means聚类算法进行任务分配后，将50个打磨点分为两类，分别交给机器人A和机器人B进行打磨，如图10所示。

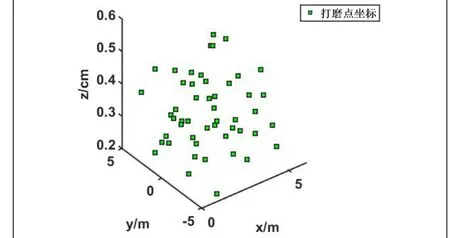
图 9 初始打磨点分布图

图 10 打磨点任务分配图

4.2 打磨点排序算法仿真

为验证提出的TSP-混合PSO算法在对打磨点的排序优化问题上的可行性，本文基于MatLab平台进行该算法的仿真验证。设置粒子群规模分别为经K-means算法所分配给机器人A和机器人B的打磨点为30和20，最大迭代次数100。TSP-混合PSO算法将打磨点分配结果按照路径最短的原则进行排序，规划结果如图11、图12所示。

图 11 机器人A规划的打磨路径图

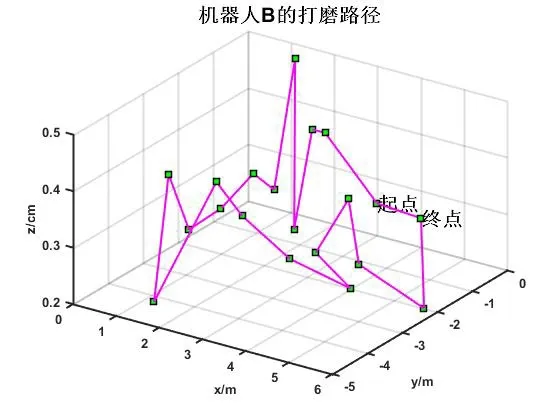
图 12 机器人B规划的打磨路径图

同时，为了验证TSP-混合PSO算法性能的优劣，本文将标准粒子群算法和TSP-混合PSO粒子群算法进行了比较，结果如表1所示。

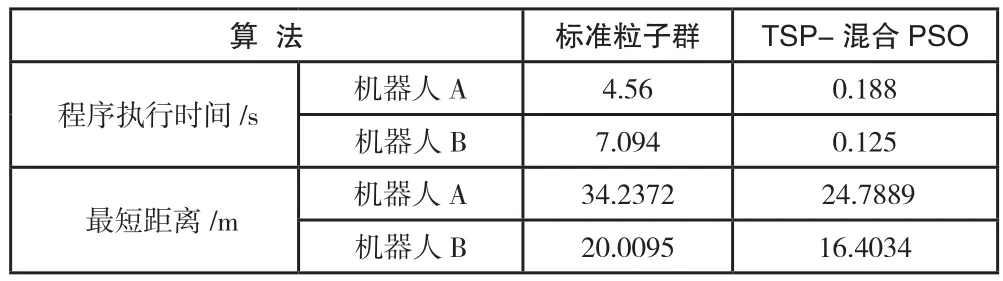
表1 标准粒子群算法和TSP-混合PSO粒子群算法的比较

从表1可以看出，本文提出的TSP-混合PSO算法在程序执行时间以及路径长度方面的效果均优于标准粒子群算法。

4.3 机器人避障规划仿真

通过ROS中设置障碍物，该障碍物包括上述的两种情况，即以港机大型构件中的横梁、桁架为障碍物以及双机器人协同作业时互为障碍物。如图13所示，在没有选择RRT*算法进行避障规划时，机器人直接穿过横梁到达目标点。而利用RRT*算法进行避障规划后，仿真结果显示通过RRT*算法进行避障规划所形成的路径，如图14所示，可以看到，机器人由起点到达终点完全避开了横梁和桁架等障碍物。双机器人协同作业时的避障规划如图15所示，机器人在执行打磨任务时成功避开了另一机器人。

图 13 机器人无避障路径图

图 14 机器人避障路径图

图 15 双机器人作业时的避障规划图

5 结语

针对港机大型构件结构特点，本文首先利用K-means算法对多机器人打磨点进行任务分配，然后基于分配结果，提出TSP-混合PSO算法对单台机器人打磨点进行优化排序，得到港机大型构件机器人打磨任务分配和路径执行顺序结果，解决了机器人打磨由于打磨点多以及打磨点的不确定性而带来的任务分配以及路径排序困难。同时，针对港机大型构件机器人的打磨路径规划中存在的两种避障难题，本文结合RRT*算法，实现了港机构件的横梁、桁架为障碍物以及双机器人协同作业时互为障碍物的可靠避障。