一类带约束的双调和方程的非平凡解

张术慧

(福建师范大学 数学与信息学院，福建 福州 350117)

1 引言及主要结果

本文考虑带约束条件的双调和问题：

(Ⅰ)

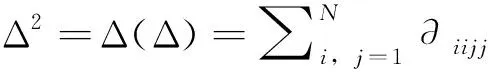
i)f∈C0(Ω×R，R)，f(x，t)t≥0，存在零点的领域U使得对任意的t∈U{0}，x∈Ω都有f(x，t)t>0；

许多学者讨论了带约束的非线性椭圆问题：

(1.1)

李[1][2]假设λk是-Δ的第k个特征值，对于α>0或α<0时，就λ=λk+1，λk<λ<λk+1，λ≤λ1三种情况讨论了上述问题解的存在性和多解性。钟等[3]通过构造一个新的结构得到了当f带有超临界指数项的情况时(1.1)存在三个解的结果，并在[4][5]中将这一结果延拓到带有算子Δp的方程中。

近年来双调和问题正在被广泛的讨论，关于双调和方程Dirichlet边界问题：

(1.2)

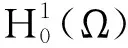
我们先给出一些记号和定义。

令：λ1是f=0时问题(1.2)的第一特征值。由文[10]中的(3.2)式有λ1>0。设：

(1.3)

(1.4)

(1.5)

本文主要结果有：

定理1.1f满足条件i)ii)，当α>0，λ<λ1时问题(I)存在非平凡弱解。

定理1.2f满足条件i)ii)，且F满足：

当α<0，λ=λ1时问题(I)存在非平凡弱解。

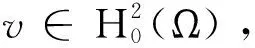
(1.6)

2 当α>0，λ<λ1时

本文中C表示常数，在不同的地方其值不同。

命题2.2[12，Proposition2.1.3]若meas(Ω)<∞，H:Ω×R→R满足Caratheodory条件：

1)对几乎所有的x∈Ω，H(x，u)是u的连续函数；

2)对每一个u，H(x，u)是x的Lebesgue可测函数。

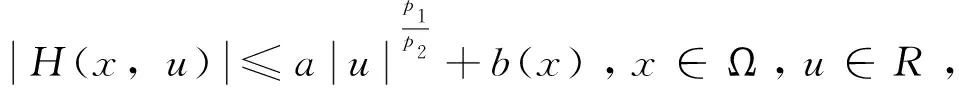
其中a>0，p1，p2≥1是常数，b(x)∈Lp2(Ω)。那么，Caratheodory映射f:u(x)∈Lp1(Ω)H(x，u(x))∈Lp2(Ω)连续。

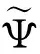
证 需要注意的是：

(2.1)

先证明Ψ'(u)，Φ'(u)存在。

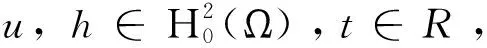
从而Φ在u处沿方向h的方向导数为：

(2.2)

由Lagrange中值定理，则存在θ=θt，x∈[0，1]使得：

由于f满足假设ii)，则

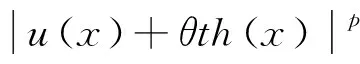
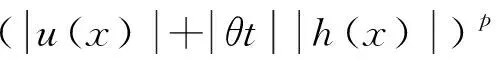
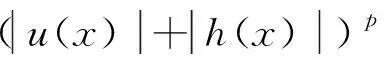
当t→0时，f(u+θth)→f(u)在Ω内几乎处处成立。因此由Lebsgue控制收敛定理可得：

故Ψ在u处沿方向h的方向导数为：

(2.3)

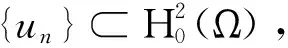
(2.4)

再由

(2.5)

对于任意的uk∈Nα，〈Φ'(uk)，uk〉=2α≠0，因此Φ'(uk)≠0。而由于Ψ'(u)，Φ'(u)连续，则β连续得证。

引理2.4 当λ<λ1时有以下结论

若i)ii)的假设成立，我们有以下结论：

2)Ψ'是全连续的；

3)Ψ是弱连续的。

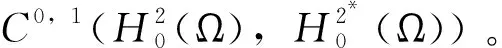
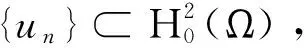
3)因为条件ii)，存在常数a1，b1使得

(2.6)

这就说明了映射Κ:u(x)∈Lp+1(Ω)F(x，u(x))∈L1(Ω)。又由不等式，令u，v∈Lp+1(Ω)，存在常数C1，C2，C3使得：

故于(2)证明相同可得，

Ψ(un)-Ψ(u)

因此Ψ弱连续。

任意u∈Nα都有

由于Nα有界，由Sobolev嵌入定理，命题2.1及(2.6)式可知在Nα上Ψ(u)有界，因此c>-∞。

(2.7)

因此0>c>-∞。

以下命题来自于[13，Theorem7.12]和[13，Remark7.12]。

命题2.7 设E是Hilbert空间，设J∈C1(E，R)存在G∈C1，1(E，R)使得

M=G-1(0)，G'(u)≠0，∀u∈M

(M)

若J在M中有下界且满足PSm条件，其中

则m可达到，且存在z∈M使J(z)=m，

定理1.1 的证明：

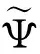
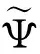
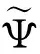
(2.8)

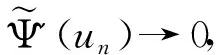
由于βn有界且下界不为0，则存在收敛子列仍记为βn，有βn→β0≠0。因为Ψ'全连续，由上式可得:

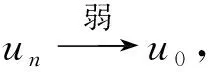
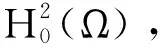
3 当α<0，λ=λ1时

定义算子K:

这就说明了K是全连续的。

对于任意u，h∈H，t∈R，

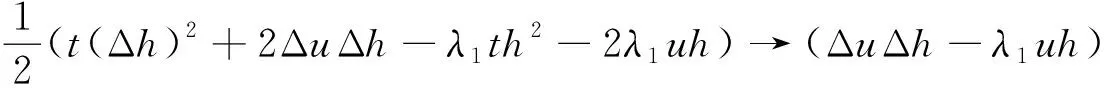
因此，

〈Φ(u)，h〉H=〈u，h〉H-λ1〈Ku，h〉H

(3.1)

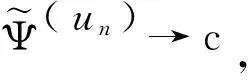
证 因为un⊂Nα，则:

(3.2)

根据条件iii)，

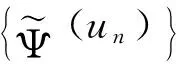
由于Nα有界，由Sobolev嵌入定理，命题2.1及(2.6)式可知在Nα上Ψ(u)有界，因此c>-∞。与命题2.5类似证明可以得到0>c>-∞。

设un⊂Nα使得:

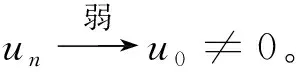
故由(3.2)式可得

因此u0≠0。

由(2.9)式及(3.1)式能够得到:

由(2.8)式后的证明同样有βn有界且下界不为0，则存在收敛子列仍记为βn，有βn→β0≠0。因为Ψ'，K全连续，则由上式可得: