独立与相依情形下加权广义线性模型选择的重对数律和强一致性
杨晓伟,赵开斌,刘相国,王冬银
(巢湖学院 数学与统计学院,安徽 合肥 238000)
Nelder(1972)[1]提出了一种线性组合扩展模型,即广义线性模型(GLM)。GLM提供了一种统一的具体方式来估计具有不同分布假设的各类模型。只需假设概率模型依赖于指数分布族,便可将模型构建分解为规范(协变量和回归参数)的线性预测变量项,以及将线性预测变量映射为期望值的联系函数。到目前为止,在我们常用的概率表述中,概率模型描述了Y的随机成分,而线性预测变量则表示了系统性成分。线性预测变量和联系函数强调了GLM是均值或预测响应的模型,其条件是协变量和参数。反向联系函数用于将线性预测值映射到适合于假定的概率模型区间,它将线性预测变量与条件均值联系了起来。
人们常常将GLM划分为自然联系和非自然联系两种函数类别。针对拥有自然或非自然联系的广义线性模型最大似然估计的渐近正态性已有相关理论证明,具体参见Fahrmeir和Kaufmann(1985)[2]。但渐近正态性是一种弱的收敛性定理,且利用重对数律(LIL)推导强一致性的文献有很多。另外在线性回归的背景下最先引入了许多优良的算法,但关于它们的理论性质以及用于逻辑回归和其他广义线性模型的优化方法一直被研究。van de Geer(2008)[3]证明了L1惩罚的高维GLM的oracle不等式,而Fan和Peng(2004)[4]研究的oracle性也适用于GLM。Huang和Zhang(2012)[5]研究了惩罚GLM方法的优化算法。这些算法的计算复杂度通常以p线性增长。Zheng和Peng(2017)[6]根据加权Lasso变系数分位数回归估计,应用重对数律对BIC-型模型选择的一致性进行了研究。
对于许多实际回归问题,多余或无关的变量可能会进入模型中,这样估计量的有效性将会大大降低。在科学分析获得回归系数之后做变量选择是不可避免的。通常地,当考虑证明模型选择的一致性时,如果像BIC、系数估计的弱相合性甚至强相合性均是不充分的,将不能得到收敛速度。因此估计量强一致性的收敛速度即LIL是值得关注的。在独立同分布噪音假设下(可能是非正态),Rao和Wu(1989)[7]对具有非正态噪音线性模型的模型选择一致性应用了LIL。类似地,Wu和Zen(1999)[8]对线性模型研究了Huber的M-估计量。
由于相依观测情况下加权广义线性模型的研究现有文献鲜有涉及,故本文重点研究了相依情形下综合性更强、应用性更广的加权GLM相关统计性质,且允许存在众多指数分布族或联系函数。在某些简单的GLM中,自然联系函数并不能总是提供最优的拟合。例如,负二项回归作为非自然联系型GLM可以拟合过离散计算数据,而泊松回归作为自然联系型GLM难以应用于此类计算数据。McCullagh(1989)[9]指出,由于自然联系函数的先验信息没有被充分利用,故多数情形下选取非自然联系更为合适。通过文献调查可知,Qian(2010)[10]仅仅分析了某些GLM的特定情形(即具有自然联系的泊松回归)。本文的研究将在Qian(2010)[10]分析基础上进行拓展。
此外,本文将讨论具有非自然联系函数类型GLM的模型选择强一致性。由于前人关于GLM的研究很少考虑到具有非自然联系函数类型,因此本文主要贡献是在一些温和条件下推广前人的研究结果,从而达到良好的模型选择性能。验证模型选择的一致性等价判断惩罚项的阶数是否介于O(log log n)与O(n)之间,见定理4。
1 加权广义线性模型
dFyk=C(yk)eykθk-bθkdv(yk),Cyk>0,k=1,…,n.
(1)
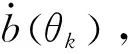
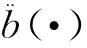


(2)
则其得分函数为
(3)
有关GLM更多讨论,可查看Chen(2011)[12]。此外,Efron和Hastie(2016)[13]为当今大数据和计算环境提供了有关现代统计推断的令人耳目一新的观点。
1.1 非自然联系函数的例子
下面将给出拥有非自然联系函数的GLMs的例子。
(1)Probit模型
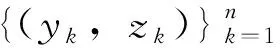
与逻辑回归类似,Probit模型中u(·)和b(·)遵循如下参数方程:
(2)负二项回归模型
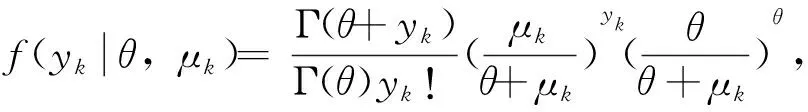

对于NBR中u(·)和b(·)的关系如下:

1.2 加权得分方程
在估计回归系数时,一种普遍认可的稳健方法是加权似然法。该方法分配一系列权重用来扰动每个样本在对数似然函数中的贡献,即基于某些加权函数,n个样本权重同时变化而产生的GLM稳健估计量。

则加权最大似然估计(MLE)为
(4)

考虑关于β的向量导数,令
则加权得分函数为

(5)
及关于β的Fisher信息阵
(6)
2 模型选择准则
2.1 基础知识与符号标记
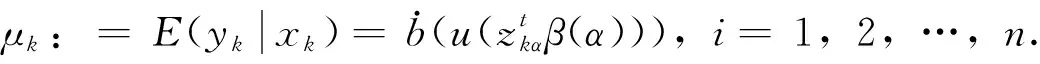
因此,易获得基于GLMs似然的目标函数,当m充分大时,可使用上述任一种模型选择方法估计出所有子模型的精确度。本文中仅考虑了给定维数的情形,而在增长维或高维情形下的模型选择准则已被研究过了,可参见Kim和Jeon(2016)[14]。
现定义:
(7)

(8)

2.2 条件和结论
(H.1)设λ1{S}…λm{S}为m×m维对称矩阵S的m个有序特征值,{In(β0)}为Fisher信息,满足,i=1,…,m;(ii)∃d1,d2>0,满足d1nλp{In(β0)}d2n.
(H.2)非随机设计的有界设定:对所有i,假定‖zk‖:L,L>0.
(H.3)假定所有参数β∈Rm,满足


注意到AB意味着B-A是非负定的,则严格特征值条件成立:其中Im是p维识别矩阵,cl,cu是正的常数。
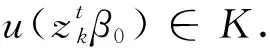

(9)

2.3 独立情形下的强极限理论
定理1 在H.1到H.4条件下,对任意修正模型α∈Αc,有
(10)

定理2 在与定理1同样条件下,对任何非修正模型α∈Αw,有
(11)

根据定理1,2的结果,可知对于所有修正模型α∈Ac的最大对数似然都是几乎必然大于全模型的未知真实对数似然且它们差的界受到|O(loglogn)|限制。然而,对于所有非修正模型α∈Aw的最大对数似然都是几乎必然小于完整模型的未知真实对数似然,同时,当n充分大时,它们差的界受到|O(n)|限制。对于模型选择准则几乎必然会选择最简单修正模型的,我们称之为强一致性。而对于仅仅几乎必然会选择出一个修正模型的,称之为一致性。具体的讨论如下定理。
定理3 若一个广义线性模型满足条件(H.1)~(H.4),则对于模型选择BIC和SCC准则都是强收敛的,而对于AIC准则是收敛的但不是强收敛。

2.4 相依情形下的重对数律
在经济学和金融学中,当使用短期自相关将响应作为时间序列数据进行收集时,严重依赖于样本独立性的假设是不合理的。鉴于大多数研究GLM的现有参考文献仅针对独立数据而已,而相依数据在很大程度上未被涵盖。Fan等(2016)[17]已对具有相依误差线性模型进行了研究。而与具有相依响应的线性模型相比,强调相依误差或相依响应的GLM很少被研究,参见Koll(2019)[18]。本节将重点介绍弱相依响应GLM,即
k=1,2,…,n,
(12)
其中εk是具有零均值的弱相依误差序列且zk是被固定的。

(13)
对于(13)式解的推断是一个典型例子,且是独立响应的最大似然估计。关于拟似然估计的更多细节可查阅Fahrmeir和Tutz(2001)[19]。应用重对数律,采用针对独立观测情形中提到的类似方法来推导模型选择的一致性。为更好呈现相依关系结构,现给出一些用于度量相依关系的符号和定义。
设(Ω,F,P)为概率空间,B,C是F的子σ-域。设L2(B)是所有具有有限二阶矩B-可测随机变量的一个子集。下面介绍ρ-混合和α-混合系数(强混合系数)的概念。
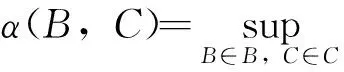
(14)
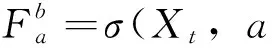
n→,则称随机序列{Xt,t∈}为α-混合或者强混合。如果
n→,则称随机序列{Xt,t∈}为一个ρ-混合过程。若对任何两个子集随机序列B,C⊂且过程{Xt1,t1∈B}和{Xt2,t2∈C}是相互独立的,则称平稳随机变量序列{Xt,t∈}为m-相依。要注意的是,当α(A,B)时,ρ-混合过程将变成α-混合过程。为简单起见,本文研究将严格限制在平稳序列上。
要证明相依情形下的渐近理论还需额外的正则假设。
(H.5)yk满足ρ-混合条件且具有几何衰减ρ(n)=O(r-n).
(H.6)yk满足m-相依。
由于弱相依性使问题变得更复杂,故假定设计矩阵X为非随机矩阵。Fan(2016)[17]也给出了类似的假设。与Fan(2016)[17]中的条件3不同,他们假设的α-混合指数衰减速率为α(m)=O(e-amb),其中a,b为正常数。但本文提出的几何衰减率比指数衰减率要慢一些,说明本文的响应相依性更强一些。应注意,对于(H.6)如果一个m-相依序列,当m>n时,有ρ(n)=O(r-n),则该序列是ρ-混合的,但它可能不是具有几何衰减速率ρ(n)=O(r-n)的ρ-混合。另外,(H.6)表明ρ-混合对于某些序列an具有截断衰减速率ρ(n)=O(an·1{nm}).
下面给出相依情形下重对数律的结果。

(15)
进一步,∃d>0,有

3 相关定理的证明
本文证明关键是对负对数似然函数的数学分析与二次函数局部逼近。主要困难是如何标准化加权得分函数,及如何几乎准确地建立两个对数似然函数差的一致渐近界限。主要证明技术是集中不等式及文献中广泛采用的对数似然比的误差界,具体参见Wu和Zen(1999)[8]。Qian(2010)[10]也有类似的考虑。
首先,定义正的序列ηn,满足
ηn↑和
(16)
由ηn定义L2球序列且半径与ηn成正比:Bn={β:‖β-β0‖且表示它的边界,则B1⊃B2⊃B3⊃…⊃Bn.进一步,由β和β0定义两个对数似然的对数似然比:


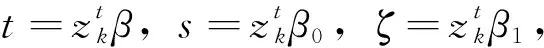
=:R1n(β)+R2n(β)+R3n(β)
(17)

证明之前先给出几个引理和推论,这些结果在证明定理1~4中用到。
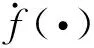

(18)
其中Cu,Cl为正的常数。

推论1 若条件(H.1)~(H.4)成立,对j=1,2,…,p,则
(19)

(20)
这里1p:=(1,…,1)t.
(21)
(22)
因此满足了引理3的条件(i),由(9)式可知引理3中(ii)也成立。故推论1得证。
推论2的证明:观察可知推论2的结果显然来自推论1,证明过程与推论1类似,这里不再赘述了。
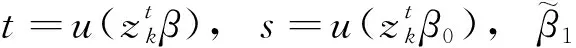
(23)
上式最后一个等式使用了泰勒公式。则
(24)

R1n(β)I(β∈∂Bn)=O(1)(β-β0)t
≥O(n)‖β-β0‖2I(β∈∂Bn)
(25)

(26)
对于R2n(β),由柯西不等式和LIL,则
|R2n(β)|I(β∈∂Bn)
=O(ηn)loglogna.s.
(27)
对于R3n(β),再次使用柯西不等式,则
(28)

(29)
则由Kn(β,β0)的定义,对于全模型,要证明(10)式即证下面的不等式
(30)
(31)
接着,根据推论1和定理1条件,则
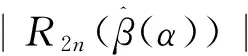
=O(loglogn)
(32)

=O(loglogn)a.s.
(33)
根据(31)式、(32)式和(33)式,则

=O(loglogn)a.s.
故定理1得证。
(34)
定义:B0={β:‖β-β0‖这里α0∈Αc是具有最小维度的真实模型。很显然B0是一个紧集,对于任意错误模型α∈Aw,由有对于全模型,几乎必然是B0的一个内点,当n充分大时,应用Kn(β,β0)的凸性质,则有
(35)

(36)
利用引理2,条件(H.1)~(H.4)和(31)式,则
R1n(β)I(β∈∂B0)≥O(n)‖β-β0‖2I(β∈∂B0)
(37)
类似地,利用(32)式,有
R2n(β)I(β∈∂B0)
(38)
取上确界得
(39)
同样地,利用(33)式,有|R3n(β)|I(β∈∂B0)
当n充分大时,取上确界得
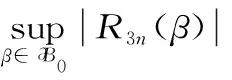
(40)
根据(36)式,则
(41)
定理3的证明:当条件(H.1)~(H.4)成立时,考虑将α分为两种情况,即α∈Αc或α∈Αw.
步骤1:对任意正确模型α∈Αc,由定理1的证明,我们有
找出使Sn(α)取得最小值的α,即
(42)


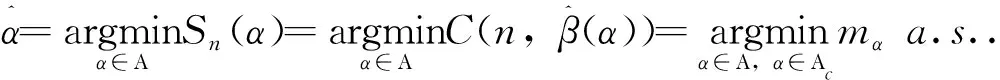
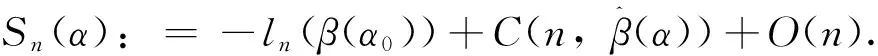

定理4的证明:为证明的方便,我们需要三个额外的引理,即分别对于ρ-混合过程和m-相依响应的两个LIL结果及Davydov’s不等式。
引理4 (ρ-混合过程的LIL,Lin和Lu(1997)[22]的推论9.2.1)设{Zn,n≥1}是一严格平稳ρ-混合序列且
引理5 (m-相依随机变量的LIL,Chen(1997)[23])设{Zn,n≥1}是一实平稳强混合序列,满足E(Z1)=0,


对于ρ-混合响应或m-相依响应情形LIL的证明与独立情形有点不同,主要不同之处在于计算得分函数的方差,即不能忽略作为协方差部分的非零交叉项的影响。
(1)先考虑ρ-混合序列情形:对于j=1,…,p,令

(43)
引理6 (Davydov’s不等式)设
且EXp<,EYp<(p-1+q-1<1),则
EXY-EXEY参见Lin和Lu(1997)[25]引理1.2.4)
通过上述Davydov’s不等式,令引理6中的p=q=3,则有
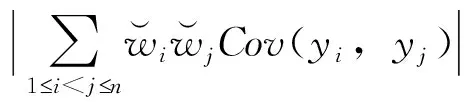
根据(H.5),误差序列εi满足ρ-混合条件且具有几何衰减速率ρ(m)=O(r-m),α-混合系数与ρ-混合系数满足关系:α(n)则
=O(1)[nO(1)-O(1)]=O(n).
(44)
由于In(β)(k,k)=O(n)→,因此引理4的条件(i)被满足。由于假设条件(H.5)可知ρ(n)=O(r-n)=O((logn)-1-ε),则表明引理4的条件(ii)也被满足。
(2)再考虑m-相依序列情形:对于j=1,…,p,则
在(H.6)条件下,可将LIL的结果应用于具有m-相依响应的真实平稳强混合序列,参见引理5。由上述可知用于α-混合或m-相依加权得分函数的LIL为
因此,结合引理3,可由独立情形LIL证明过程推导出,对∀α∈Αc有
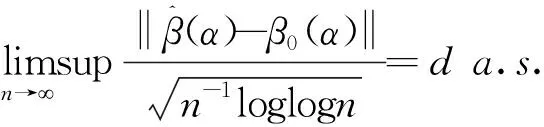
4 结论

应用类似本文的方法,针对广义线性模型字样估计的BIC准则也具有模型选择的强一致性,可参见Ai,Yu和Zhang(2018)[24]。该工作的下一步可考虑在某些温和条件下,研究广义线性模型的变量误差最大似然估计的重对数律,而Miao和Yang(2011)[25]仅研究了线性回归的情形。

