改进蚁群算法在解决TSP问题中的应用
李 雪,王 雷
(安徽工程大学 机械与汽车工程学院,安徽 芜湖 241000)
旅行商问题(Traveling Salesman Problem,TSP)是典型的组合优化问题,在实际应用中具有重要作用,比如在飞机的航线设定、物流配送、集成电路的整体布局、车辆路径等领域已经得到了广泛应用,因此研究旅行商问题具有重要意义。为解决旅行商问题,国内外学者提出了很多算法,如遗传算法、粒子群算法、蚁群算法等智能算法[1-3],其中蚁群算法在解决旅行商问题中具有较强的优势。蚁群算法是由意大利学者Dorigo M首先提出的,该算法是一种启发式算法也是仿生进化算法,通过对蚂蚁觅食时的行为进行模仿来寻找一条从初始点到终点的最优路径。但是蚁群算法也具有许多缺陷,如收敛速度慢、易陷入局部最优解等问题[4]。目前国内外许多学者在解决TSP问题提出了许多优化方案,文献[5]中提出了一种改进的遗传算法,引入贪心算法以及选择操作来解决旅行商问题,有效地解决了传统遗传算法的易陷入局部最优解问题,文献[6]通过将遗传算法和模拟退火算法相结合的方式来找到TSP最优解,文献[7]引入对数递减的权重对萤火虫算法的位置进行更新,同时结合了遗传算法的选择、交叉以及变异等操作来提高算法的搜索能力,利用改进的萤火虫算法求解TSP问题。文献[8]设计了一种自适应局部调整算子和全局随机策略的布谷鸟算法来求解TSP最优解。文献[9]通过对IGT算法进行改进,引入原有映射算子、Inver-over算子和求异算子来求解TSP问题。
针对以上问题以及国内外学者提出来的解决方案可以看到利用改进的算法在TSP问题上仍然需要进一步优化,尤其是在解决收敛速度以及局部最优解等问题上。本文中使用的改进算法是基于传统蚁群算法的基础上进行改进,首先通过自适应改变挥发系数来使初始时刻的蚁群搜索能力加强、范围扩大、避免陷入局部最优解、提高其鲁棒性,其次将轮盘赌算子利用到状态转移规则中,有效地提高了解的质量和算法的收敛速度,最后通过精英选择操作,有效地提高了算法的全局搜索效率和收敛速度。以上改进的蚁群算法对不同时刻的信息素都有着全局掌控能力,为提高收敛速度和避免局部最优解提供了保证。最后利用改进的蚁群算法(Improved Ant Colony Optimization,IACO)来解决TSP问题,并且完成了仿真实验,相比其他的改进算法的实验结果可以证明本文的改进蚁群算法的可行性和优越性。
1 改进蚁群算法
1.1 自适应调整挥发系数ρ
蚁群算法在运行过程中会受到许多因素的影响,本文所提到的动态调整参数ρ来解决算法在运行过程中收敛速度慢、易陷入局部最优解等问题。当挥发系数ρ设置比较大时,之前蚂蚁走过的路径被再次选择的机会就会加大,过小时会提高全局搜索能力导致收敛速度降低。于是初始时刻将参数ρ设置为最大值,虽然以前搜索路径被再次选择可能性加大,但是信息正反馈占主导作用。
本文对参数ρmin设置为0.1,C为随机常数,ρ的自适应调整公式如下:
(1)
1.2 多型状态转移概率的融合
轮盘赌算法在遗传算法中经常使用,于是将轮盘算子应用到城市转移状态规则中,适应度越大,该个体被选中的概率也就越大,对于解的质量有很大提高,也有助于提高算法的收敛速度。
(2)

1.3 精英选择较优路径信息素更新
当全部蚂蚁都完成一次路径搜索以后,按每个蚂蚁行走路径的长短进行排序(L1≤L2≤L3≤…≤Lm),每只蚂蚁对信息素更新的贡献根据该蚂蚁的排序进行加权,加权值记为φ。更新公式(3)、(4)和(5)如下:
τijt+1=1-ρτijt+Δτijt
(3)
(4)
(5)
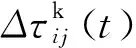
1.4 较优路径节点交叉操作
如果蚁群在每次迭代后无法获得最优解时,则认为蚁群算法可能处于停滞状态,陷入局部最优解,因此通过对来自不同节点的路径进行交叉操作来获得最新路径,如下图所示,改进算法的全局搜索效率得到了显著增强。
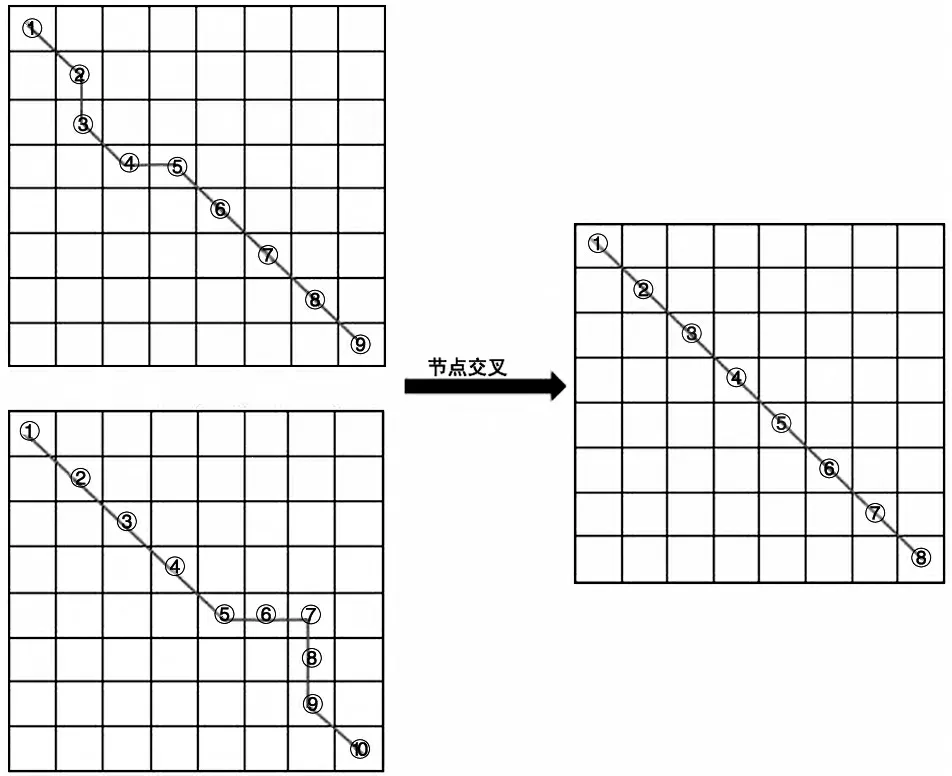
图1 节点交叉操作
2 IACO求解旅行商问题
TSP(旅行商问题)是一个组合优化问题,可以通过数学模型简单的描述为:假设有n个城市,可用1,2,…,n来表示每个城市,每两个城市i和j之间的距离为dij且已知,每个城市恰好被遍访一次且刚好是一条闭合回路,其中回路路径总长度最短。其数学模型表达如下:
(6)
(7)
(8)
(9)
式中:n为城市数量,式(6)为目标函数,式(7)和式(8)表示经过每个城市且只有一次,式(9)表示无子回路解的产生。
IACO解决TSP问题步骤可表示如下:
Step 1 初始化蚂蚁参数,将起始禁忌表tabuk设为空集。
Step 2 采用公式(1)来设定初始值C进而自适应调整挥发系数ρ。
Step 3 采用公式(2)来按照新状态转移概率选择下一个节点加入禁忌表。
Step 4 判断蚂蚁是否周游结束,如果周游结束则蚂蚁k=k+1,否则返回到Step3步骤。
Step 5 判断蚂蚁k是否等于M,是则进行下一步骤,否则返回到步骤Step 2。
Step 6 计算路径长度Lφ并对其排序,然后采用公式(3)、公式(4)、公式(5)进行信息素更新。
Step 7 判断是否满足结束条件,是则结束输出结果,否则进行较优路径节点交叉操作,然后判断是否满足结束条件,是则输出结果,否则返回到步骤Step 1,直至循环结束。
具体算法流程图如图2所示。
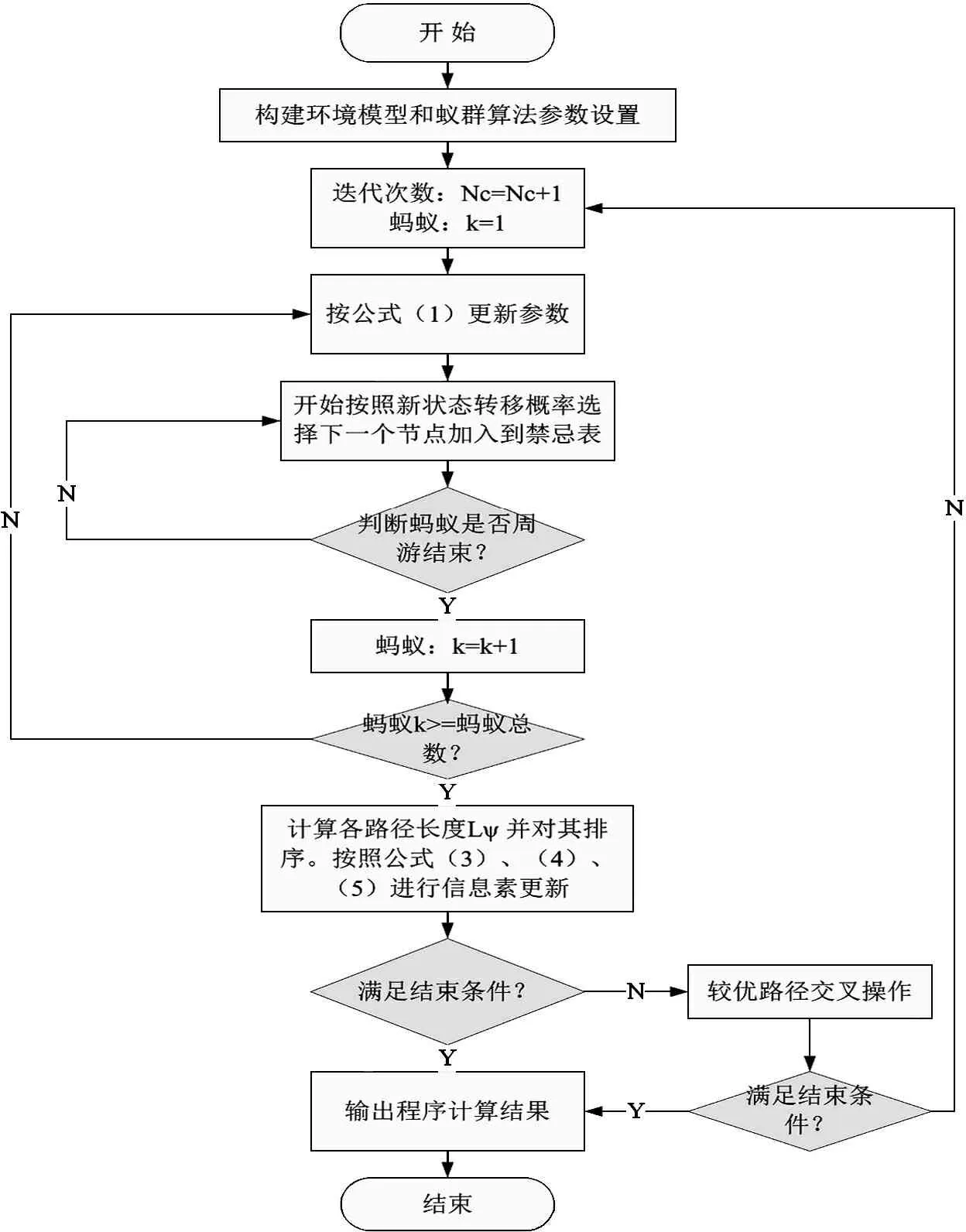
图2 改进蚁群算法流程图
3 实验结果与分析
为了验证本文改进的蚁群算法的可行性,将本文算法应用在多组TSP案例中,同时和传统的蚁群算法和其他学者改进的蚁群算法做一个比较来证明本文改进的蚁群算法的优越性。实验环境是在windows7操作平台上运行MATLAB2016a软件将GA、HA、IGA、ACO和IACO进行比较。算法的参数设置为:蚁群总数M=50,常量C=0.9,参数α=1.5,β=7,信息素常量Q=10,最大迭代次数Nmax=100。仿真结果分别如图3-图6所示。

图3 Att48优化实例

图4 Eil51优化实例
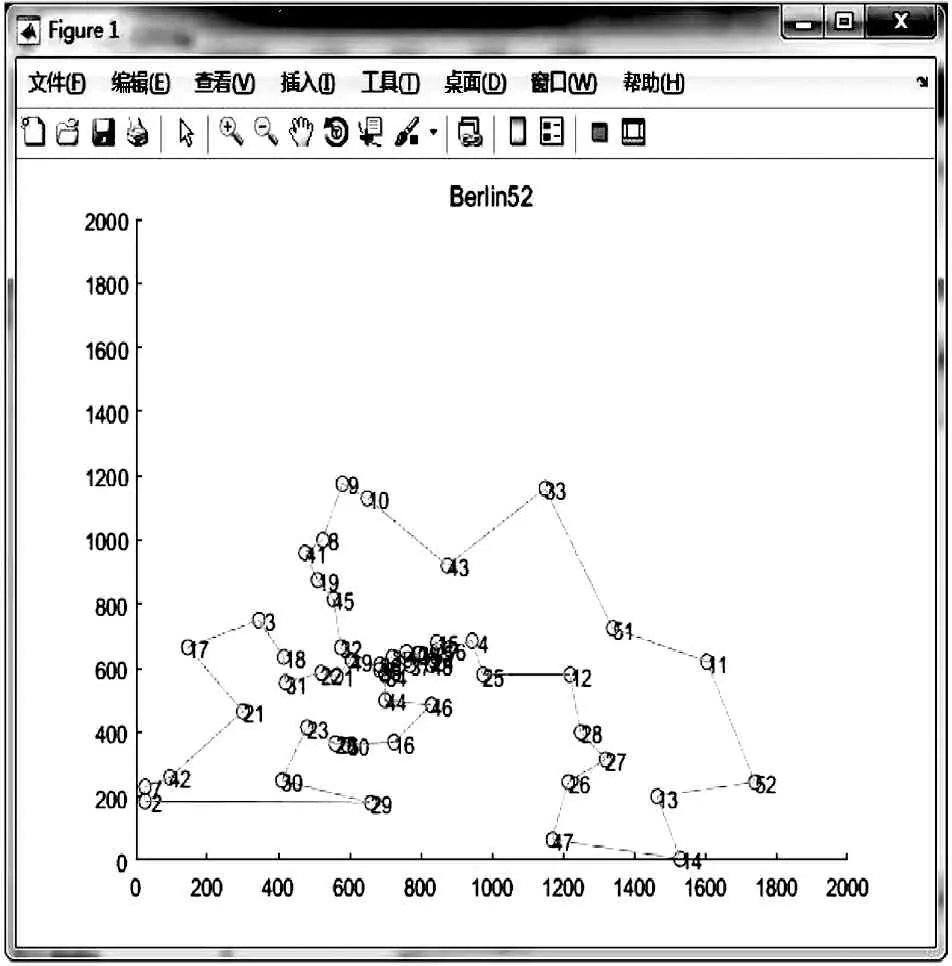
图5 Berlin52优化实例

图6 Pr76优化实例

表1 实验结果对比
如图3~图6所示,本文通过对比文献[10]中四个案例Att48、Eil51、Berlin52、Pr76,分别采用GA、HA、IGA、ACO和IACO求解TSP问题,结果如表1所示。从表1可以看出本文的IACO在求解TSP问题平均最优值上和最优解更加相近,证明了本文IACO的有效性和可行性。

图7 kroA100优化实例
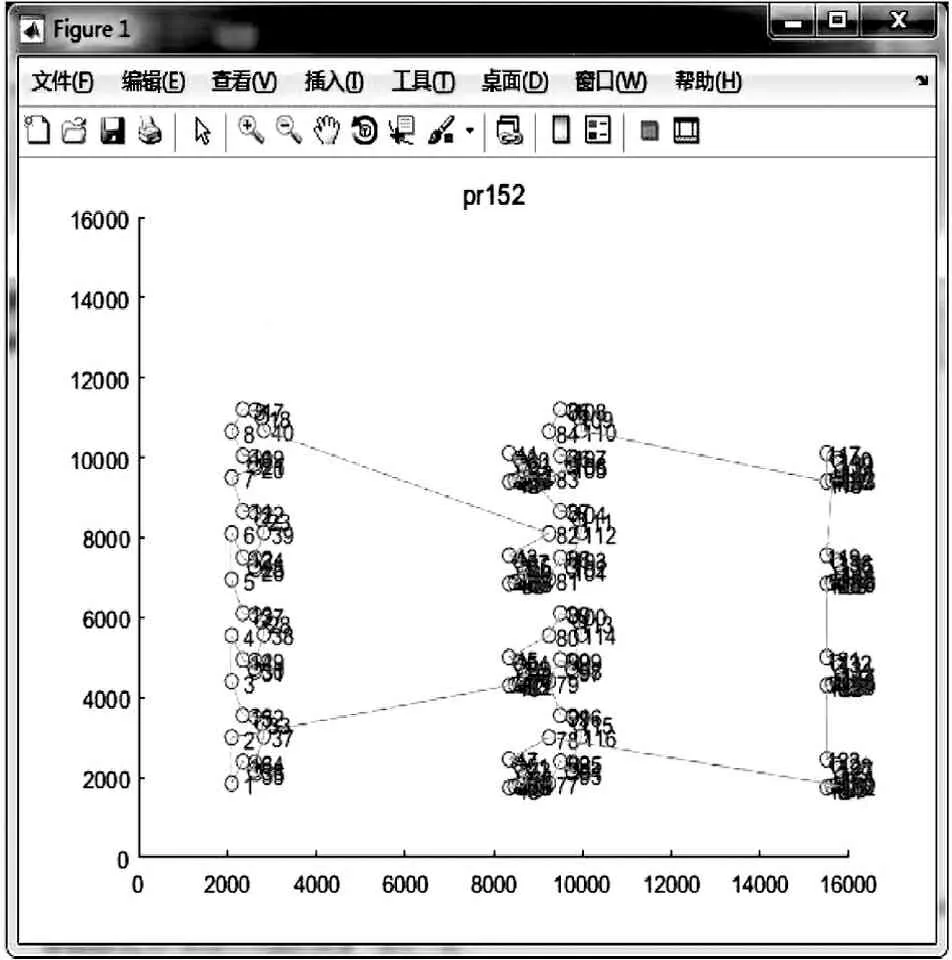
图8 pr152优化实例
为了更好证明本文改进算法的有效性,将IACO与ACO做了如下对比,将两种算法分别在kroA100和pr152中运行,结果分别如图7-图8所示。IACO在案例kroA100和pr152中得到的解明显比ACO更加接近最优解。在案例kroA100中ACO的平均偏差在7.7%,IACO的平均偏差在2.3%,在求解精度方面IACO较ACO有70%的提高。在案例pr152中ACO的平均偏差在10.2%,IACO的平均偏差在7.6%,在精度方面IACO较ACO有26%的提高,有效地证明了IACO的可行性。
4 结论
为解决传统蚁群算法在收敛速度慢、易陷于局部最优解等问题,本文提出一种改进的蚁群算法(IACO),首先通过自适应改变挥发系数来使初始时刻的蚁群搜索能力加强、范围扩大,避免陷入局部最优解;其次将轮盘赌算子利用到状态转移规则中,有效地提高了解的质量和算法的收敛速度;最后通过精英选择操作,有效地提高了算法的全局搜索效率和收敛速度。在解决TSP问题上,通过对比文献可以得到本文IACO在寻优能力上得到了提高,有效地避免了出现重复回路的现象,在与其他算法的比较中可以发现本文算法在解决TSP问题上具有优越性和有效性。

