不可压磁流体方程在柱坐标下的表示及其基本能量估计
钟建新,赖祥威
(1.宜春学院 应用数学研究中心,江西 宜春 336000;2.昆明理工大学 理学院,云南 昆明 650500)
流体力学方程(Naiver-Stokes方程),是2000年由美国克雷研究所召集世界上一流科学家提出的世界七大难题之一,简称百万美元问题。Naiver-Stokes方程主要给出了流体在一定区域内速度,压强以及密度之间的关系。如果还考虑到磁场对流体的影响或流体本身是带电粒子,则它们之间的关系由磁流体力学方程(简称MHD方程)给出。该方程作为现代数学的重要研究对象,在航空航天、石油开采、水利工程领域运用十分广泛[1],倘若能将磁流体力学方程研究透彻,对基础科学的贡献将是巨大的。
本文将运用微积分运算,得到磁流体力学方程在柱坐标中的表达式,进一步利用基本能量方法得到柱对称磁流体力学方程基本能量估计。这为后续的解的存在唯一性,正则性等,提供了一个保障。不可压MHD方程组描述了流体在磁场的作用下流体的运动规律,可以由下面方程描述[2]:
(1)
其中关于时间和空间的未知函数u表示流体的速度,p表示流体受到的压强,B表示磁场强度,μ表示流体的粘性,ν为磁扩散系数。粘性系数和磁扩散系数一般是关于密度和温度两个变量的函数,但本文中只考虑常数情形。其中(1)式的第三个方程表示该流体是不可压缩的,即所谓的不可压条件。关于该模型的研究实际上已经比较广泛了[3-10],但在本文中我们考虑该模型在初值条件下柱对称情形的基本能量估计。假设满足下面的初值和远场条件:
(2)
首先,需要利用坐标变换把模型(1)化简成柱对称下的方程。
1 符号说明
下面对本文涉及到的符号作如下说明,直角坐标系下梯度算子:拉普拉斯算子:把它们作用于速度场表示直角坐标系上的基向量,r0,θ0,z为主坐标的基向量。
2 柱坐标下的MHD方程的表示
2.1 柱坐标下的算子
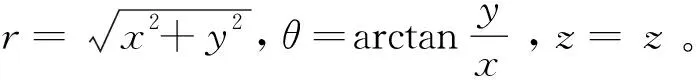
以及
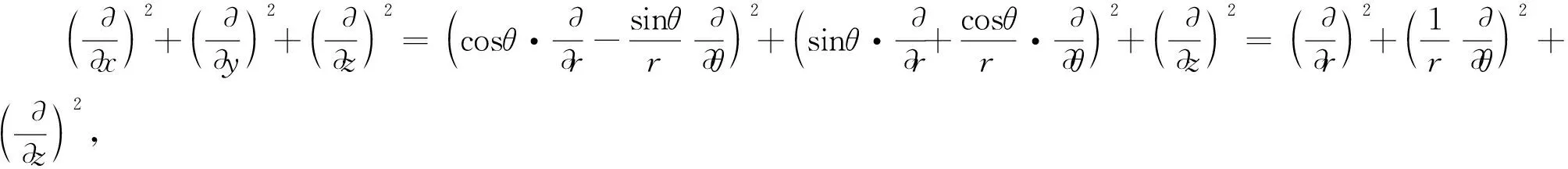
因此,可以得到拉普拉斯算子Δ在柱坐标下的表达式:
2.2 MHD方程在柱坐标下的表示
有了上面的准备,下面可以给出磁流体力学方程在柱坐标下的表达式。首先,对于对流项
对于能量耗散项,利用柱坐标下的拉普拉斯算子表达式有
显然,对于磁场方程的类似项有类似的表示形式。
对于磁流体方程的其他项,可以直接化成柱坐标下的表达式。本文只考虑无旋情形,即将所有变量看成与角度无关的函数。把上述等式相加,按r0,θ0,k整理合并可得柱坐标下的磁流体方程以及不可压条件:
3 柱坐标下磁流体方程的基本能量估计
正如前面所说,考虑方程的适定性,基本能量有界是一个基本要求,而所谓的基本能量即未知函数的L2范数,在物理里面体现为流体的动能。
定理4.1 柱坐标下的不可压无旋磁流体力学方程(3),当满足边界和远场条件(2)时,任意时刻有如下有限能量估计,其中|
证明:利用通常的能量方法,将上述柱对称磁流体力学方程前6个方程分别乘以urr,uθr,uzr,Brr,Bθr,Bzr,可以得到下述方程
将上述方程组相应的项整理合并相加,再将新方程在空间区域[0,)×[0,1]积分可得:
下面我们对上述等式右端的每一项进行逐项估计。对于Ia,利用分部积分以及远场条件,事实上我们有
Ia中其他两项也可以类似处理。因此,可以得到:
类似的,我们可以得到以下结果:
对于Ic,利用分部积分和不可压条件以及远场条件有:
同样对于Id,我们可以得到:
对于Ie,我们可以得到:
对于最后一个积分If,由不可压条件可以得到:
将上述六个等式相加,可以得到:
对于上述等式,将等式两边关于时间t在0,T积分可以得到柱对称磁流体力学方程的基本能量估计:

