轮式车载防空导弹行进间发射动力学仿真分析

李 超，王学智，李 敏

（空军工程大学防空反导学院，西安 710043）

0 引言

具备行进间发射能力的防空武器系统不仅能提高自身的生存能力，还能为陆地机械化部队提供不间断的伴随防空。机动能力对导弹系统自身生存能力的提高，宁昕［1］和朱亚红［2］等人作出了详细论证。在技术研究上，2003 年，闵建平等人［3］就作了自行高炮的行进间射击动力学研究；谢润，杨国来等人［4-5］研究了自行高炮行进间射击炮口响应，并且研究了存在耳轴-轴承的间隙时的炮口响应；2005年，赵波，范子杰［6］对防空导弹行进间发射技术的使用意义、装备特点和关键技术进行了总结，国内的防空导弹行进间发射技术的研究才开始有论文的体现；钟洲等人［7］研究了B 级和C 级路面上导弹行进间发射的安全发射车速；丰佩等人［8］研究了车载火箭炮行进间发射，简单分析了发射装置的动态响应和速度对发射规律的影响。

对于导弹行进间发射动力学的研究整体缺乏，研究内容较少。本文搭建了三维路面模型和8×8轮式车载防空导弹多体动力学模型，进行了静止和行进间发射的仿真实验，得到了导弹弹射对车体的影响和影响导弹出筒偏航速度、偏航角速度、俯仰角速度的因素。为下一步的改进奠定了基础。

1 三维路面重构

路面不平度的重构有多种方法［9-10］：积分白噪声法、AR（ARMA）模型法、谐波叠加法。本文选用谐波叠加法对三维路面进行重构。谐波叠加法源于谱估计的周期延拓假设，基于三角级数求和，采用以离散谱逼近目标随机过程的随机模型，能用于各等级随机路面的模拟，具有较好的适应性和较高的精度。

路面位移功率谱密度Gq（n）的拟合表达式［11］：

式中：n 为空间频率，单位m-1；n0为参考空间频率，n0=0.1 m-1；Gq（n0）为参考空间频率n0下的路面谱密度值，称为路面不平度系数，单位m3；w 为频率指数，为双对数坐标上斜线的斜率，决定路面谱的频率结构。

通过公式的变换，由谐波叠加生成的路面不平度数学模型［12］（三维路面谱的仿真与建模）：

时间频率范围f=0.33～28.3 Hz，将f 区间均匀划分为200 份，则N=200；（x，y）为空间点位；αi（x，y）为随机数，均匀分布于［0，1］。

根据以上数学模型，利用MATLAB 生成路面模型，如图1 所示。

ADAMS 路面有多种路面文件格式［13］，等效容积路面适合建立具有随机特性的三维路面。MATLAB 生成的路面点有规律的构成三角形，无数个三角形平面构成了ADAMS 中的路面，如图2 所示。由此生成的ADAMS D 级路面模型如图3 所示。

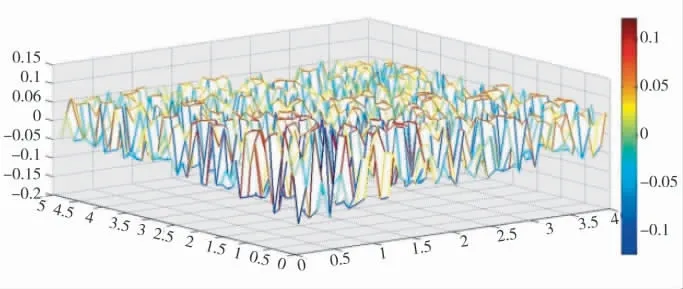
图1 MATLAB 随机路面模型图

图2 ADAMS 3D 等效容积路面模型示意图

图3 ADAMS 路面模型图

2 行进间发射动力学模型

2.1 车体拓扑结构

本文模型为8×8 轮式底盘、垂直发射的防空导弹武器系统。动力学模型分为两个部分：运载车体和导弹弹射系统。运载车体包括车轮、悬架、下车体和上车体部分；导弹弹射系统由导弹箱和导弹组成。

其拓扑结构如下页图4 所示。各部件之间的连接关系如下：J11，J12，…，J18 为轮胎和路面的接触碰撞关系；J21，J22，…，J28 为轮胎与悬架支撑杆的旋转副；J301，J303，…，J315 为上悬架与支撑杆的旋转副连接；J302，J304，…，J316 为下悬架与支撑杆的旋转副连接；J41，J42，…，J48 为上悬架与车体的旋转副连接；J51，J52，…，J58 为下悬架与车体的旋转副连接；J61 为下车体与上车体的固定副连接；J71，J72 为上车体与导弹发射箱的固定副连接；J81，J82，…，J88 为导弹箱与导弹的固定副连接，其J81 包含接触碰撞关系。

2.2 车轮模型

轮胎是车辆至关重要的部分，其基本功能包括：支撑整个车辆；与悬挂元件共同作用，抑制由路面不平引起的振动与冲击；传递纵向力以实现加速、驱动和制动；传递侧向力，为车辆提供转向。因此，轮胎模型将对整体的仿真产生很大影响。在ADAMS/View 的环境下，Tire Force 模块提供了多种轮胎模型用于车辆不同行驶工况的仿真计算，下页表1 为各轮胎模型所适用的计算工况［13］。

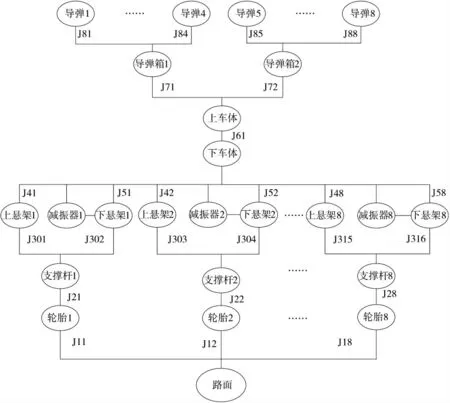
图4 模型拓扑结构图

表1 轮胎模型适用工况对照表

本文仿真实验内容为直线行进车体振动，不涉及平顺性和耐久性分析，因此，采用UA 轮胎模型。UA 轮胎模型属于纯解析模型，所需要的实验测试数据较少。UA 轮胎文件包括标题数据块、单位数据块、模式数据块、尺寸数据块、参数数据块和断面形状数据块。本文中实验模型的轮胎参数数据：轮胎自由半径0.62 m；轮胎名义断面宽度0.375 m；径向刚度870 000 N/m；径向阻尼50 Nms/m。完整的动力学模型如图5 所示。

2.3 行驶驱动和导弹弹射

车辆的行驶通过车轮的旋转驱动来实现。车轮与悬架之间设置了旋转连接副，对旋转连接副施加旋转驱动，轮胎与地面相作用，使车辆向前移动。通过数据生成速度变化曲线，利用AKISPL 曲线插值函数将速度变化曲线赋值到旋转驱动。

导弹采用弹射方式，导弹在提拉杆推力的作用下，从导弹箱内弹出。由于导弹在导弹箱内开始处于闭锁状态，当提拉杆推力达到一定数值时，闭锁装置解锁，导弹开始相对导弹箱运动。推力通过AKISPL 插值函数实现。

3 仿真实验结果与分析

本文针对行进间发射过程中导弹与车体的相互作用和相互影响进行研究。选取平整路面静止、D级路面以10 km/h 速度行进和D 级路面20 km/h 速度行进3 种工况条件进行导弹弹射仿真实验。在平整路面静止条件下弹射导弹可作为与行进间发射的参考比对对象，较好地反映行进间发射的特点。

在平整路面静止条件下导弹弹射，在导弹弹射力的作用下，导弹沿导轨弹出。车体和导弹的响应如图6～图9 所示。从图6 和图7 可以发现，车体的振动幅度值与垂向振动值存在小偏差。轮式车静止条件下的弹射，车辆在前后和左右方向也存在一定的振动，相比于垂直方向的振动较小。图8 和图9表明，导弹在出筒过程中，导弹与导弹箱导轨之间的接触碰撞使导弹产生了前向和侧向的速度偏差，但偏差值较小。前向和侧向在振动过程的最大值分别为33.3 mm/s 和24.3 mm/s，出筒时刻的值分别为17.1 mm/s 和11.1 mm/s。其值在导弹正常弹射的可接受范围内，导弹能正常弹射。

车辆作为导弹的运载和弹射平台，在导弹弹射过程中，车辆的状态将直接影响导弹姿态和运动状态。在行进的过程中，随机路面与车轮的相互耦合使车辆产生随机振动。在行进间导弹发射的过程中，不同时刻，导弹在出筒后其特性不相同。

因为D 级路面可以更好地模拟使用的恶劣路况环境，因此，仿真路面等级选定为D 级路面，速度选定为10 km/h 和20 km/h。对车辆运动10 s、11 s和12 s 时刻分别进行导弹弹射仿真实验，观察车体在垂向的振动情况和导弹在出筒时刻的速度分量、偏差角度以及角速度。

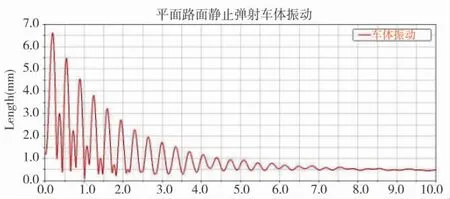
图6 车体振动幅值图

图7 车体垂向振动图

图8 车辆前向导弹速度分量

图9 车辆侧向导弹速度分量

图10 为整个仿真过程中车辆的垂向振动加速度情况。通过图片可以发现，在车辆启动时刻和10 s左右垂向加速度振动幅度较大，10 s 附近的峰值时刻为10.24 s。可以得出导弹弹射对运动中的车辆特性具有一定的影响，但相对小于来自路面的影响。

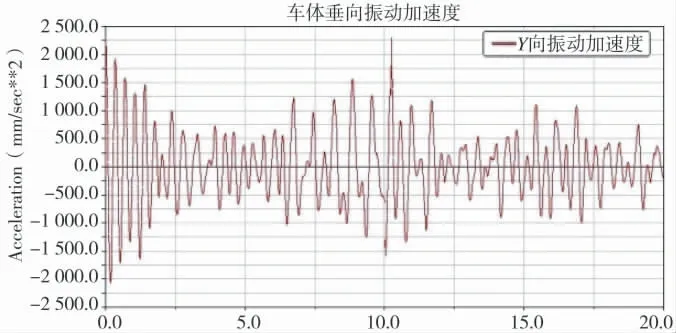
图10 车体垂向振动加速度

图11 和图12 为导弹在车辆前向和侧向上的速度分量。导弹在弹射前的速度与车体速度相同，在弹射时刻导弹与车体相互碰撞，前向和侧向两个方向的速度相对车体速度发生变化，在出筒后速度稳定。出筒后的速度与弹射时速度相差不大，因此，弹射时刻车体前向和侧向速度对导弹前向和侧向速度起到极大影响作用。

图11 10 km/h 车辆前向导弹速度分量

图12 10 km/h 车辆侧向导弹速度分量

图13 为行进间导弹弹射过程中导弹角速度曲线。角速度曲线在弹射前与车体角速度保持一致，在弹射过程中俯仰角和偏航角依然与车体保持一致，在接近出筒时刻才出现较小波动，导致导弹的俯仰和偏航角速度与出筒时刻车体的状态相接近。滚转角速度受接触碰撞影响较大，在弹射过程中产生剧烈变化，不能发现出筒时刻导弹滚转角速度与车体状态的直接关系。由于出筒后角速度不为0，故出筒后导弹自身会发生转动，导弹姿态处于变化中。

图13 10 km/h 导弹角速度

由于不同时刻车体振动状态不相同，导弹弹射出筒时的状态也会有很大差别。表二为D 级路面条件下，以10 km/h 和20 km/h 的速度行进，在10 s、11 s、12 s 时刻弹射出筒，导弹的出筒速度、角度和角速度的大小。

表2 导弹状态参数

由于前向为车辆运动方向，故导弹前向运动速度基本与车辆运动速度一致。侧向速度最大值为

145.94 mm/s，其数值相对较小，对导弹出筒后运动轨迹影响不大。导弹在出筒时刻角度较小，这是由于导弹在筒内时受导轨固定，且导弹从解锁到出筒时间短，因此，角度偏差累积量较小。车体的振动和接触碰撞使导弹具有了一定的转动角速度，由于转动角速度的存在，在出筒后导弹的姿态将发生极大的变化，甚至导致导弹弹射的失败。

4 结论

本文通过建立轮式车载防空导弹行进间发射动力学模型，对平整路面静止弹射和D 级路面10 km/h、20 km/h 多种工况进行仿真实验，并对实验结果进行详细分析，得出导弹出筒时刻状态的主要影响因素。该实验研究通过建立三维路面和动力学模型，相对于数值分析更具有参考价值，实验考虑了模型静止时的发射工况和相同工况不同时刻对导弹发射的影响。通过对仿真实验的结果分析，可以得出如下结果：

1）行进间发射系统在静止条件下发射过程中，其车体和导弹有一定的振动，但振动较小，不足以使导弹发射失败。车体发生振动，振动幅度的最大值约为6.61 mm，垂向振动幅度最大值为5.5 mm。导弹在弹射过程中因接触碰撞，导弹前向和侧向速度产生无规律变化，出筒后前向与侧向速度保持不变，振动过程的最大值分别为33.3 mm/s 和24.3 mm/s，出筒时刻的值分别为17.1 mm/s 和11.1 mm/s。

2）在D 级路面条件下，以10 km/h 速度行进，导弹弹射的弹射力会对加大车体的振动加速度，使振动加剧。但弹射力小于轮胎与路面接触碰撞产生的作用力，弹射力对行进间车体的振动造成的影响较小。导弹在弹射前处于随车振动中，导弹出筒时刻的状态与车体在弹射过程中的状态密切相关。导弹的前向速度与侧向速度，是在弹射时刻车体前向和侧向速度的基础上产生一定量的偏移，但偏移相对较小。由于车体振动赋予了导弹一定的角速度，导弹俯仰和偏航角速度与出筒时刻的车体角速度基本一致，滚转角速度在弹射过程中因为剧烈的碰撞接触，在弹射过程中快速振动变化。

3）当以10 km/h 在D 级路面上行驶，其导弹弹射出筒时的偏航角速度和俯仰角速度小于5°/s，故导弹能正常发射。当以20 km/h 在D 级路面上行驶，其俯仰和偏航角速度变化范围较大，俯仰角速度出现了11.42°/s。这将使导弹在空中的点火和控制引导产生极大的困难，因此，以20 km/h 在D 级路面行驶，导弹弹射可能会弹射失败，导弹在后续不能正常工作。

影响行进间发射中导弹的出筒状态的两个因素：一是运载车辆在行驶中的振动特性；二是导弹箱和导弹之间的接触碰撞。因此，通过提高运载车辆的减振能力将提高行进间导弹弹射对地域的适应能力。在本文研究的基础上，加入减振控制，提高车辆的减振能力，促进导弹行进间发射技术的发展与成熟。