博弈条件下基于SINR 的制导雷达波形设计*

郑家毅，翁木云，李 伟，许 强，徐泽华

（空军工程大学信息与导航学院，西安 710077）

0 引言

制导雷达发射波形优化是提高制导雷达对目标检测性能的关键因素。与传统的以接收机为中心的信号处理方法不同，利用雷达回波获取的目标与环境先验知识优化发射波形可充分利用雷达波形的各个频率，真正体现了自适应的特征。随着电子战技术快速发展，制导雷达与目标间博弈日趋激烈，不仅制导雷达可自适应地优化其发射波形，而且装备有电子对抗系统的目标能够截获雷达波形，智能地释放干扰。但现有波形优化文献大多基于智能雷达与非智能目标的假设开展研究，无法有效提高现代电子战环境中制导雷达对目标的检测性能。因此，在制导雷达与目标相互博弈条件下如何选择波形优化策略，以提高制导雷达对目标的检测性能成为当前极为重要的研究问题。

现有波形优化方法可根据优化准则分为3 类：MI、MMSE 和SNR。文献［1］中首次采用信息论针对确知目标设计雷达波形，最大化目标脉冲响应与雷达回波间的互信息量。文献［2］给出了一种MMSE与MI 间的关系，文献［3］进一步将这两种准则推广到了MIMO 雷达，并得出了结论：在高斯噪声环境中，基于MI 与MMSE 准则设计波形是等价的，文献［4］应用MI 与MMSE 准则在干扰条件下设计弹载雷达发射波形，并得到了最小均方误差准则优化波形目标识别性能优于互信息量准则的结论。然而，在色噪声条件下，由文献［5］可知基于MI 与MMSE 设计的波形是不同的。随着雷达波形带宽的不断增加，雷达的距离分辨力也在不断提升。因此，目标具有无限带宽响应的假设（即点目标）不再适用。针对扩展目标的波形设计近年来得到广泛关注。文献［6］采用最大化SNR 为准则在杂波条件下优化分布式MIMO 雷达发射矩阵，文献［7］基于SINR 与MI 准则针对确知与统计扩展模型设计波形并得到了两种优化准则间的关系。在这些成果基础上，文献［8］提出了一种在信号相关杂波条件下发射信号与接收滤波器联合优化设计的方法。文献［9-11］在杂波条件下采用PAR 与相似性约束设计波形。

以上波形设计方法均是基于雷达智能目标非智能地假设得到的研究成果。然而，在现代电子战环境中，一些目标装备有干扰系统，并能够智能地干扰制导雷达保护自身。这些智能目标可通过估计制导雷达波形参数，自适应地改变干扰频谱。自适应干扰技术以及通信系统中自适应干扰和抗干扰的相互作用一直以来都是一个热点话题［12-13］。文献［14-15］提出了通信系统中的智能干扰技术，随着这些干扰技术的发展，文献［16-17］提出了一种针对SAR 雷达的干扰技术。文献［18］基于SNR 与MI 准则设计了一种针对常规雷达的干扰优化设计方法。文献［19］基于MI 准则研究了MIMO 雷达与敌方干扰间的博弈问题，但该文只研究了点目标及噪声影响，并没有考虑杂波影响以及目标响应方差，但实际上，制导雷达波形优化策略取决于杂波及目标响应，且在发射信号较强的情况下，噪声对功率分配的影响与杂波的影响相比可以忽略不计。针对以上问题，本文主要研究电子战环境中针对扩展目标的制导雷达波形设计，在目标响应、杂波及噪声PSD 先验知识的基础上提出了3 种博弈策略模型：智能制导雷达与非智能目标、非智能制导雷达与智能目标及智能制导雷达与智能目标，基于SINR 准则分别得到了智能雷达与智能目标的优化波形。特别地，当雷达与目标均为智能时，本文给出了杂波条件下智能雷达与智能目标之间的均衡解，并基于maxmin 理论采用两步注水法得到了优化波形与干扰信号设计方案。

1 博弈条件下制导雷达信号模型

图1 博弈条件下制导雷达信号模型

设目标脉冲响应与制导雷达发射信号分别h（t）与s（t），其中目标脉冲响应为时间有限的随机模型。令H（f）与X（f）分别为h（t）与x（t）的傅里叶变换。令r（t）为接收滤波器脉冲响应，n（t）为零均值信道噪声过程，其PSD 为Snn（f），在波形带宽W 内不为零。令同类型杂波c（t）为一个零均值高斯随机过程，其PSD 为Scc（f），在W 内为常数。假设目标发射的干扰信号为j（t），其PSD 为J（f）。图1 展示了电子战环境下基于SINR 的制导雷达信号模型。

如图1 所示，在接收滤波器输出端信号y（t）为

其中，μh（f）是H（f）的均值，假设为零。则t0时刻的SINR 为

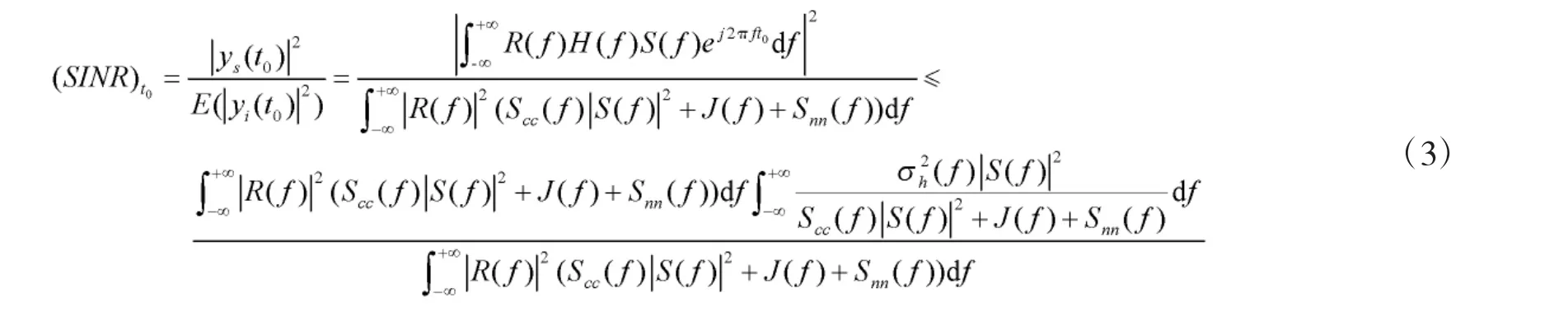
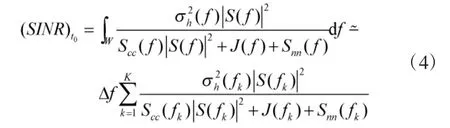
其中，W 为制导雷达与目标干扰工作频带，K 为频率采样数，Δf 为频率采样间隔。

2 博弈条件下制导雷达波形设计及检测性能分析

在电子战环境中，制导雷达与目标的互动变得越来越复杂。不同的博弈策略模型意味着不同的波形优化策略。本节分别给出智能雷达与非智能目标，智能目标与非智能雷达以及智能雷达与智能目标3 种博弈策略模型，并给出每种情况下智能一方的波形优化策略。

2.1 智能制导雷达与非智能目标

假设制导雷达是智能的并可根据环境与目标的先验知识自适应地改变发射波形，这些先验知识可通过一些认知方法获得［20］，此时非智能目标不能智能地优化其干扰波形，仅能释放压制干扰。因此，出于保守性与合理性考虑，非智能目标仅能在制导雷达频带W 内释放高斯白噪声干扰。对于此种情况，制导雷达可选择以下策略优化发射波形

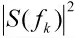
2.2 非智能制导雷达与智能目标

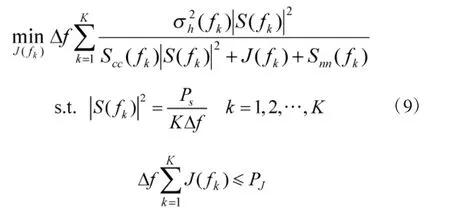
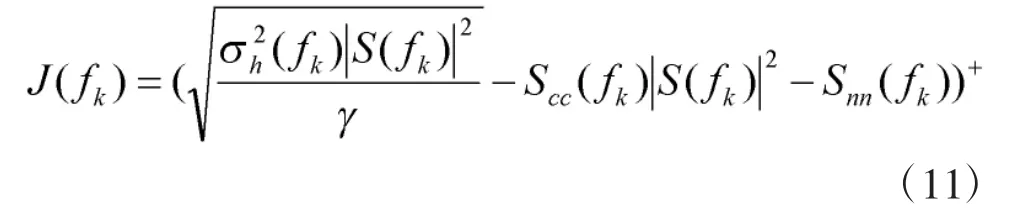
从式（11）结果可以看出由注水法得到的干扰优化信号不仅取决于制导雷达波形频谱与噪声，也与杂波有关。当制导雷达发射能量很大，杂波够强时，噪声可忽略不计。

2.3 智能制导雷达与智能目标

在现代战争环境中，最有可能出现的情况是制导雷达与目标均智能。例如，目标装备有对抗系统，该系统可侦测雷达波形参数，根据雷达信号释放干扰信号，制导雷达为现代空对空制导雷达，其可根据目标环境及接收到的干扰信息自适应地优化发射波形。在此情况下，制导雷达发射信号会被目标拦截和干扰，因此，雷达会选择一种博弈策略优化可能出现的最坏情况。该情况与文献［19］中提到的类似，即雷达在Stackelberg 博弈模型中处于领导位置。出于保守性考虑，制导雷达将选择如下波形设计策略：

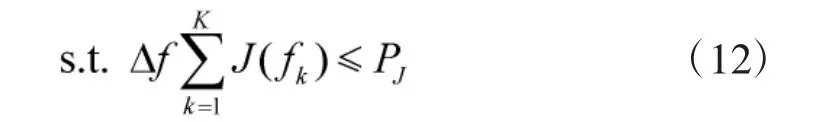
根据Sion 的maxmin 定理［21］，优化式（12）可表示为

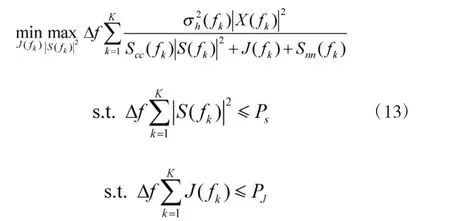
由于智能雷达可对目标的干扰信号作出最优反应，式（5）中的优化信号可应用于第1 步注水算法。基于式（8），式（13）可化简为

在此基础上，式（14）可进一步化简为：

由于雷达与目标均智能，双方均可智能、实时改变波形，为解决式（16）优化问题，首先需要找到并证明雷达与目标间的博弈均衡解。为找到均衡解，首先确定J（fk）必要，因为它是式（16）中关键所在。根据文献［19］，优化式（12）必须满足以下4 个特征才能保证达到均衡时J（fk）在干扰功率限制下得到注水解：

当制导雷达与目标达到平衡点时，出于合理性考虑，如果在某一子频带fk内无信号功率，智能目标将不会在该子频带内分配任何干扰功率，不然就会浪费有限的干扰功率。为优化干扰性能，目标将在分配有信号功率的子频带内分配干扰功率。因此，特性1）得到验证。

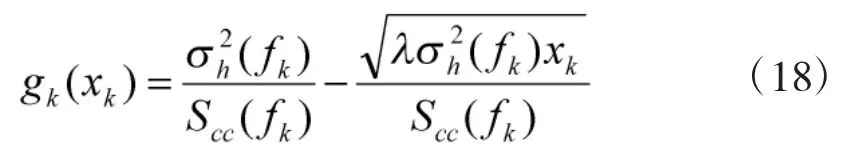
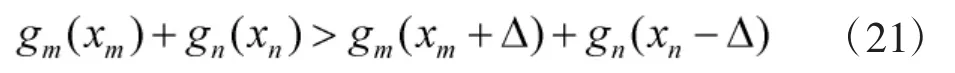
特征3）、4）同样可通过反证法证明。综合4 条特征可知，在博弈达到均衡时，式（16）可通过第2步注水法得解。此时，优化干扰信号J（fk）如下：

其中，常数γ1与1 分别由功率约束条件确定。

从以上推导过程可以看出，Stackelberg 博弈中maxmin 优化问题可通过两步注水法求解。首先雷达根据噪声、杂波及干扰分配其信号功率，然后目标将依据杂声、杂波及雷达信号应用注水法分配干扰功率。

3 仿真分析

3.1 目标干扰功率固定时性能分析

图2 智能目标干扰优化策略

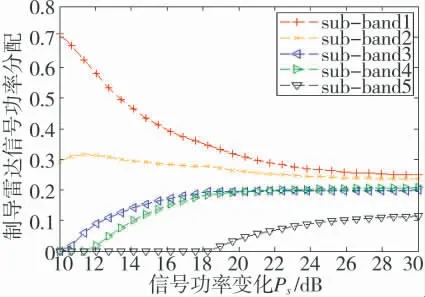
图3 智能制导雷达信号功率分配策略

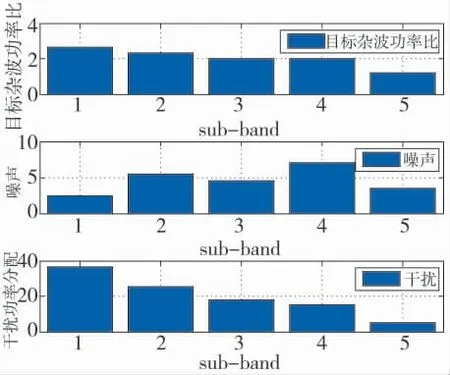
图4 智能目标对抗智能制导雷达时干扰功率分配策略

图5 智能制导雷达探测智能目标时雷达信号功率分配策略

3.2 制导雷达信号功率固定时性能分析

表1 智能制导雷达与智能目标功率分配值

图8 智能制导雷达探测非智能目标时雷达信号功率分配策略

图9 智能目标干扰智能制导雷达时干扰功率优化策略

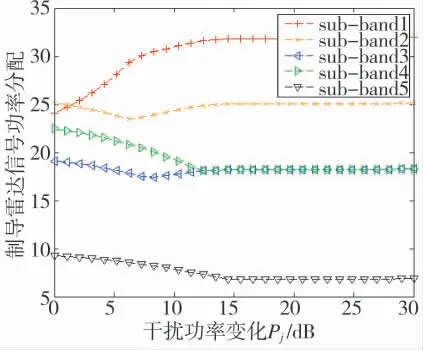
图10 智能制导雷达探测智能目标时雷达信号功率分配策略

4 结论

在现代电子战环境中，雷达与目标间博弈愈发激烈。本文研究了智能制导雷达对非智能目标、非智能制导雷达对智能目标、智能制导雷达对智能目标3 种不同博弈模型，并在杂波条件下基于SINR准则通过注水法，对每种博弈模型中智能一方进行波形优化。特别地，对于目标雷达均智能的情况，给出对抗双方的均衡解，通过两步注水法求解波形优化问题。仿真试验分别分析了不同场景中智能雷达或智能目标波形优化策略。