一种基于能量补偿修正的移相相减方法*

李雪林，王会良，许 浩

（1.洛阳职业技术学院机电工程系，河南 洛阳 471000；2.河南科技大学机电工程学院，河南 洛阳 471003；3.中国科学院声学研究所，北京 100190）

0 引言

单条拖线阵声纳在实际探测目标应用中，为分辨目标所在左右舷，需要搭载平台改变机动方向，但这种方法所需时间较长，容易丢失目标［1-4］。对此，研究学者提出利用双线阵、三元组水听器阵、矢量传感器阵实现对目标左右舷分辨。在双线阵实现对目标左右舷分辨时，常采用的方法为时延差法、噪声模型法、特征频率法、移相相加法、移相相减法等［5-8］。

时延差法［9-10］通过测量线阵波束信号之间时延差实现目标左右舷分辨，当参考阵元位置发生错位时，会造成左右舷分辨结果发生严重跳变，且在某些频点和角度上无法分辨目标左右舷；噪声模型法［11-12］是基于最优波束形成推导方法求出最佳滤波系数，使左右相应两个水听器具有心形指向性，但需要计算不同频率的最优波束加权系数，并对不同频率的信号分量进行加权，计算量较大；特征频率法［13］针对常规波束形成法在频带选取上没有考虑双线阵左右舷抑制增益问题而提出的左右舷分辨方法，存在处理系统带宽和接收信噪比矛盾问题；移相相加法［14-16］通过对左右相应两个水听器接收数据进行移相相加使其具有心形指向性，该方法所具有的最大左右舷分辨增益和最理想心形指向性与阵间距有关，在双线阵间距较小时，目标左右舷分辨效果较差；移相相减法［17］通过对双线阵中左右相应两个水听器接收数据进行移相相减使其具有心形指向性，该方法改善了移相相加法对阵间距要求，但端射方向的合成波束能量会被削减，影响对端射方向目标检测效果，对目标方位角使用范围有限。

针对移相相减法在端射方向的能量衰减问题。本文依据移相相减法所得心形指向性函数变化形式与扫描角度关系，采用能量补偿修正技术降低扫描角度对合成波束的影响。为了直观评估本文方法的有效性，本文在理论分析中给出了相应的数值仿真说明。理论推导分析和数值仿真结果均验证为，当目标位于端射方向时，相比原移相相减法，本文方法可以对目标实现有效探测；在同一衰减比下，探测能力增加了10°，增加了移相相减法对目标方位角的适用范围，具有较好的稳健性，便于工程应用。

1 移相相减法

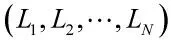
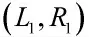
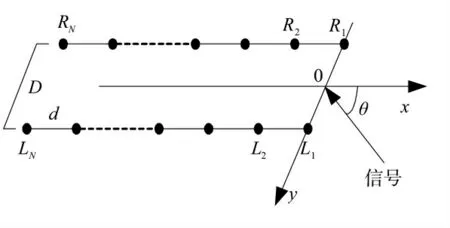
图1 双线阵各阵元位置及接收目标信号示意图

为了实现目标左右舷分辨，接下来阐述移相相减处理所得心形指向性方法。

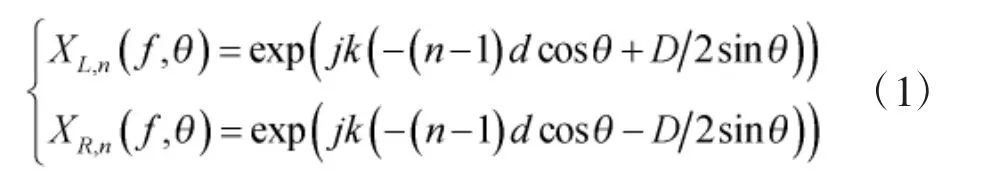
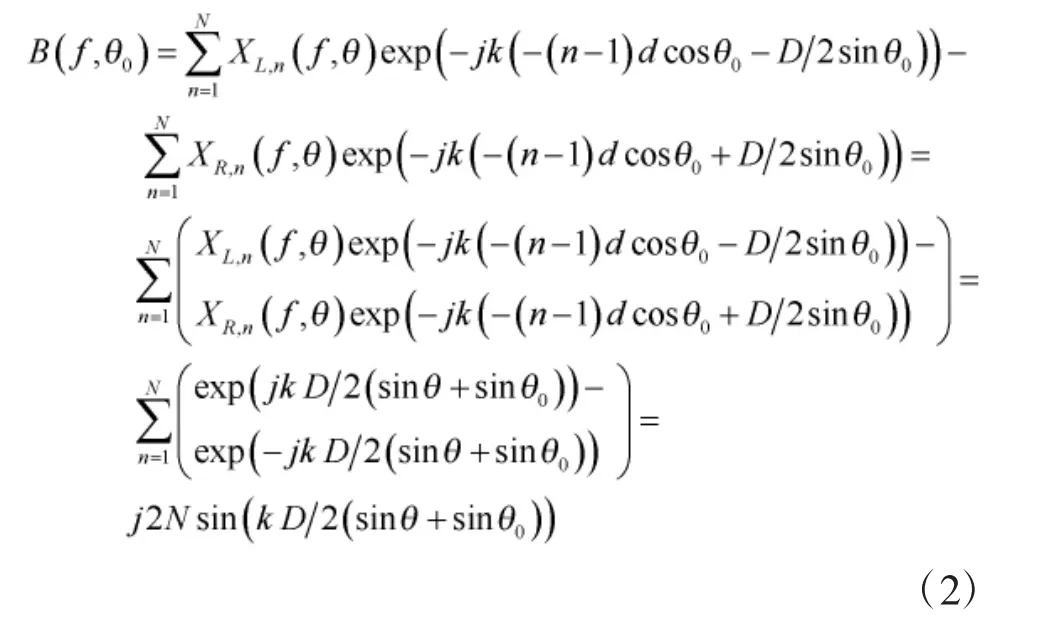
为了能够更好地表示左右舷抑制比，对上式做进一步处理，得

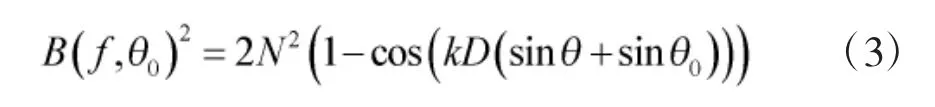
此时，目标方向θ 处的波束形成响应与可能被误判为目标方向-θ 处的波束形成响应之比为：

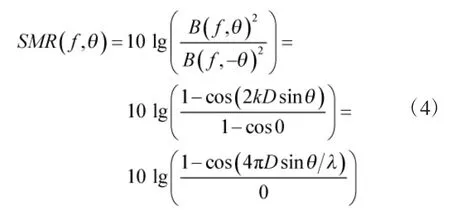
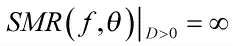
2 基于能量补偿修正的移相相减方法

2.1 衰减分析

虽然移相相减法可以有效降低分辨左右舷目标对线阵之间间距要求，但该方法在端射方向存在能量衰减问题。

由式（3）可知，对于扫描方向θ=θ0时，在目标方位θ 输出能量，除了受左、右线列阵间距D、目标辐射信号波长影响外，还受目标所在角度θ 影响。

为了更直观地说明移相相减法对同一目标信号在不同方位处合成波束能量差别，图2 为线阵之间间距D 为不同值时，由移相相减法所得同一目标信号在不同方位处被合成波束能量归一化值。

图2 同一目标信号在不同方位处被合成波束能量归一化值

由图2 结果可知，在左、右线列阵间距D 一定时，移相相减法所得同一目标信号在不同方位处被合成波束能量值差别加大，即在线阵正横方向（90°或270°）上波束能量最大，随着目标方位向端射方向移动，波束能量逐渐被衰减至0。

另外，由图2 结果还可知，对于同一目标信号在同一方位时，随着左、右线列阵间距D 减小，波束能量也随之变小，但变化较小。

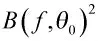
2.2 补偿方法

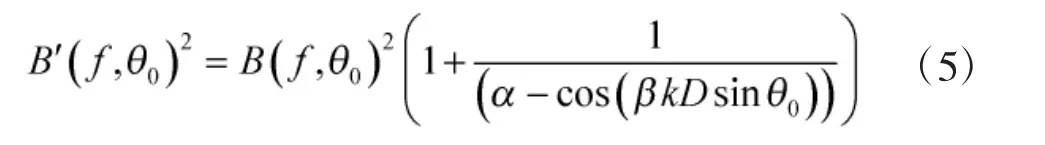
依据式（5）所示能量补偿修正技术，图3 和图4分别给出了不同左、右线列阵间距D 时的能量补偿前后结果。

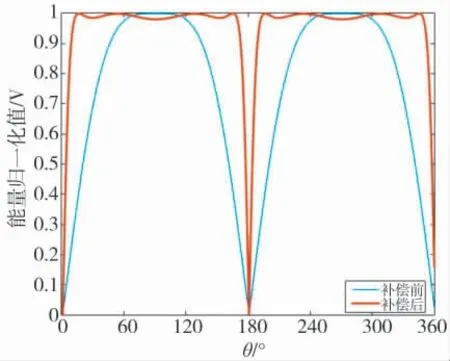
图3 同一目标信号在不同方位处被合成波束能量归一化值（）

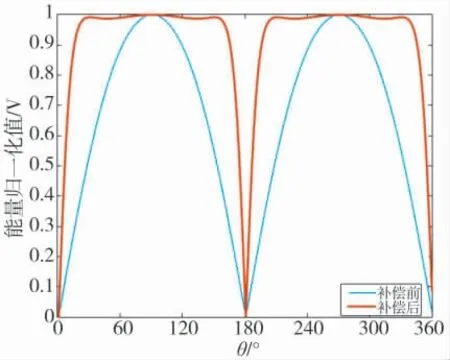
图4 同一目标信号在不同方位处被合成波束能量归一化值（）

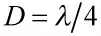
由图3 和图4 亦可知，通过能量补偿可将远离正横方向背景能量和正横方向附近背景能量趋于一致，将远离正横方向背景噪声能量和目标信号能量同时抬高，但目标位置附近局部信噪比未发生变化，经背景基底归一化处理后，可降低移相相减法中心形指向性函数由于端射方向能量衰减（背景基底降低）对端射方向目标信号检测的影响。由于能量补偿后目标位置附近局部信噪比未发生变化，所以能量补偿后对噪声敏感性并未有实质性增加，即能量补偿后远离正横方向背景噪声能量的增加并不会对目标位置附近局部信噪比产生影响，不会对端射方向的目标检测产生影响。

3 数值仿真分析

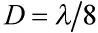
设双线阵水听器左、右线列阵均是阵元间距为d=8 m，阵元数为N=32 的等间隔线列阵，左、右线列阵之间间距为D=1.0 m，处理带宽为f =20 Hz～100 Hz，采样频率为fs=5 000 Hz，背景噪声为服从N（0，1）分布的高斯白噪声，两目标分别位于双线阵左舷侧θ1=80°、右舷侧θ2=340°，目标1、2 分别由服从N（0，1）分布的高斯信号和线谱组成，线谱与其周围连续谱谱级比为LCR1=10 dB，可保证其对输入总能量的贡献影响不大；同样目标2 线谱与其周围连续谱谱级比为LCR2=10 dB。相比背景噪声，目标1、2 输入信噪比均为SNR1=SNR2=-10 dB。图5～图8为不同方法所得方位历程图、波束图和不同时刻目标2 处波束能量。表1 为典型时刻由2 种方法所得目标2 处波束能量值。

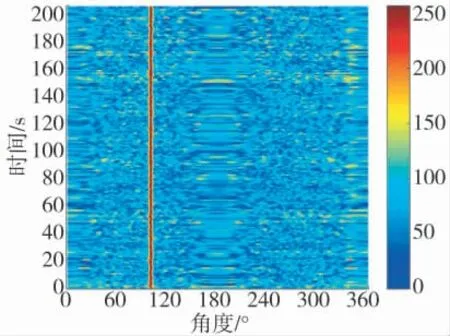
图5 移相相减法所得方位历程图

图6 本文方法所得方位历程图

图7 单一时刻波束图

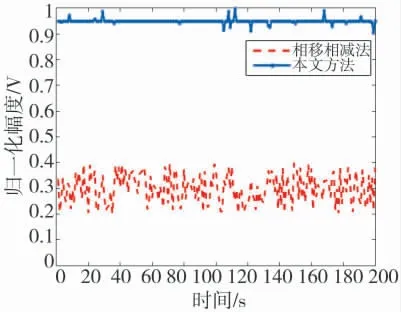
图8 不同时刻目标2 处波束能量

表1 目标2 处波束能量值

由图5～图8、表1 可知，在该仿真条件下，相比未进行能量补偿修正的移相相减法，本文方法对目标2 输出相对能量值由不到0.4 V 提升为0.9 V 以上，即通过能量补偿可将远离正横方向背景能量和正横方向附近背景能量趋于一致，经背景基底归一化处理后，可降低移相相减法中心形指向性函数由于端射方向能量衰减（背景基底降低）对端射方向目标信号检测的影响，解决了移相相减法合成波束在端射方向上的能量衰减问题，对目标2 实现了有效探测，该仿真结果与式（5）分析结果一致。

4 结论

针对移相相减法在端射方向的能量衰减问题，本文首先推导了移相相减法合成波束函数，并分析了双线阵阵间距和目标角度对移相相减法合成波束产生的影响；然后依据移相相减法所得心形指向性函数变化形式，提出了一种基于能量补偿修正的移相相减方法。

理论推导分析和仿真实验结果均表明，通过能量补偿修正技术，可有效降低移相相减法所得心形指向性函数对波束形成结果的影响；当目标位于端射方向时，相比原移相相减法，本文方法可以对目标实现有效探测；在同一衰减比下，探测能力增加了10°以上，扩大了移相相减法对目标方位角适用范围，具有较好的稳健性，便于工程应用。