符合阿贝原则的数控机床几何误差建模

赵 壮，娄志峰，张忠宁，王晓东，范光照*，陈国华，向 华

(1.大连理工大学 机械工程学院，辽宁 大连 116024；2.襄阳华中科技大学先进制造工程研究院，湖北 襄阳 441053)

1 引 言

航空航天、医疗器械等高端制造业对于零部件的精度有很高的要求，数控机床作为机械装备的母机，其加工精度的好坏直接影响被加工件的质量[1-2]，因此提高数控机床的加工精度对于发展我国高端制造业具有重要意义。几何误差作为数控机床重要的误差源[3-4]，对机床加工精度有很大影响，其补偿模型一直都是国内外研究人员的研究重点。

目前，针对机床几何误差的常用补偿模型是以多体系统理论为基础，通过齐次转换矩阵所建立的误差补偿模型，即齐次坐标转换矩阵(Homogeneous Transformation Matrix，HTM)法[5-7]。HTM法是由Hartenberg等在机构运动学的基础上提出的[8]，Ferreira等将它应用到机床几何误差补偿模型中[9]。刘又午基于多体系统理论推导出适用于三轴加工中心的误差补偿模型，通过9线法辨析几何误差，对模型的有效性进行了验证[10]。由于对直线度误差的定义不同，针对三轴机床的误差补偿模型又可以被分为两种：包含18项几何误差的补偿模型[11]和包含21项几何误差的补偿模型[12]，董泽园等对这两种模型存在的差异进行了分析，并在三轴机床上进行了补偿精度的比较[6]。粟时平推导出适用于五轴机床的几何误差补偿模型，并在虚拟加工条件下进行了加工精度的预测[13]。陈东菊、谢春等分别将多体系统理论应用于数控磨床和五轴车铣复合加工中心的补偿模型推导中并验证了模型的补偿精度[14-15]。郭世杰等基于多体系统理论建立了转台-摆轴式五轴机床的补偿模型，有效降低了转动轴几何误差对机床精度的影响[16]。

以上研究都是使用激光干涉仪进行误差测量，为降低补偿成本、提高补偿效率，有研究人员使用多自由度测量仪器替代激光干涉仪进行机床几何误差的测量，但由于测量过程不满足阿贝原则，几何误差测量结果中存在阿贝误差，严重影响补偿精度。为此，范光照、Vahebi等分析了三轴机床几何误差传递机理以及阿贝误差对于加工过程的影响[17-19]；杨建国等将阿贝臂的概念引入误差建模中[20]；向华等分析了阿贝误差对于几何误差测量结果的影响并设计了一种测量方法避免在测量结果中引入阿贝误差[21]。

HTM法因具有易理解、推导简单和适应性好等优点，而被广泛应用于机床几何误差补偿中，但使用HTM法进行误差补偿需要保证刀具切削点、几何误差测量点以及低序体坐标系原点的空间位置重合。在使用多自由度测量仪器配合HTM法进行空间误差补偿时，由于几何误差的测量点与低序体坐标系坐标原点不重合，两点间存在空间偏位，使得一部分运动轴的角度误差对于空间误差的影响没有被考虑，会降低补偿精度。

本文以XYFZ型数控机床为例，介绍HTM法的推导过程，分析其中不足；然后，基于阿贝原则与布莱恩原则分析机床空间误差传递机理和几何误差测量的不准确性，并进行验证实验；最后，对HTM补偿模型进行优化，并对优化后的补偿模型的准确性进行实验验证。

2 HTM误差补偿模型

2.1 机床几何误差

由于制造精度问题，机床运动轴在运动过程中的实际运动位姿与理想运动位姿存在偏差，此偏差被称为几何误差[22]。单根运动轴有6项几何误差，包括3项角度误差和3项平动误差[6]，分别为偏摆角误差、俯仰角误差、滚动角误差以及水平直线度误差、竖直直线度误差和定位误差，如图1所示。

此外，运动轴之间还存在垂直度误差，故三轴机床共有21项几何误差，误差表达式如表1所示。在加工过程中，这些误差的存在会导致刀具切削点的实际位置与理想位置产生偏差，影响加工精度。

图1 运动轴6项几何误差Fig.1 Six geometric errors of motion axis

表1 21项几何误差表达式

2.2 模型推导过程

首先，依照多体系统理论和低序体阵列法，将机床X，Y，Z运动轴和床身假设为存在相对运动的低序体并进行编号，机床床身为体0，Z轴为体3，X轴为体2，Y轴为体1，并在各低序体内预设一个固连坐标系，低序体坐标系设置如图2所示。然后，通过相邻低序体进行坐标转换，将刀具切削点在刀具坐标系(体3固连坐标系)内和工件坐标系(体2固连坐标系)内的相对坐标转换到机床床身绝对坐标系(体0固连坐标系)中，再通过齐次矩阵运算得出机床的空间误差[6]。

在计算空间误差时，机床导轨的理论运动值和几何误差值分别以理论运动矩阵和误差特征矩阵(表2、表3)的形式表示[5]。

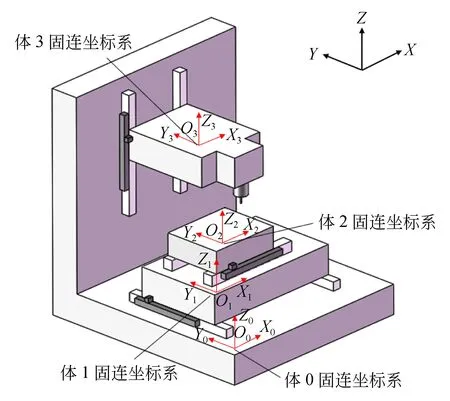
图2 XYFZ型机床结构及低序体坐标系设置Fig.2 XYFZ machine tool structure and low sequence body coordinate system

表2 理想运动矩阵和误差特征矩阵的表达式

表3 垂直度误差特征矩阵表达式

Tab.3 Characteristic matrix expression of perpendicularity error

假设刀具切削点在工件坐标系(体2坐标系)中的齐次坐标为Pw，在刀具坐标系(体3坐标系)中的齐次坐标为Pt。可得齐次坐标Pw通过坐标转换后在床身坐标系中的实际坐标值为：

Pactual-w=T01ΔT01CxyT12ΔT12Pw.

(1)

齐次坐标Pt转换后在床身坐标系中的实际坐标值为：

Pactual-t=CyzCxzT03ΔT03Pt.

(2)

故由机床21项几何误差所引起的刀具切削点空间误差为：

E=Pactual-t-Pactual-w.

(3)

2.3 模型不足

HTM法是从机构运动学中衍生出来的[9]，在使用HTM误差补偿模型对机床进行误差补偿时，必须要保证机床的刀具切削点与工件坐标系、刀具坐标系的坐标原点重合，同时保证几何误差测量点和机床运动轴的固连低序体坐标系原点的空间位置重合。

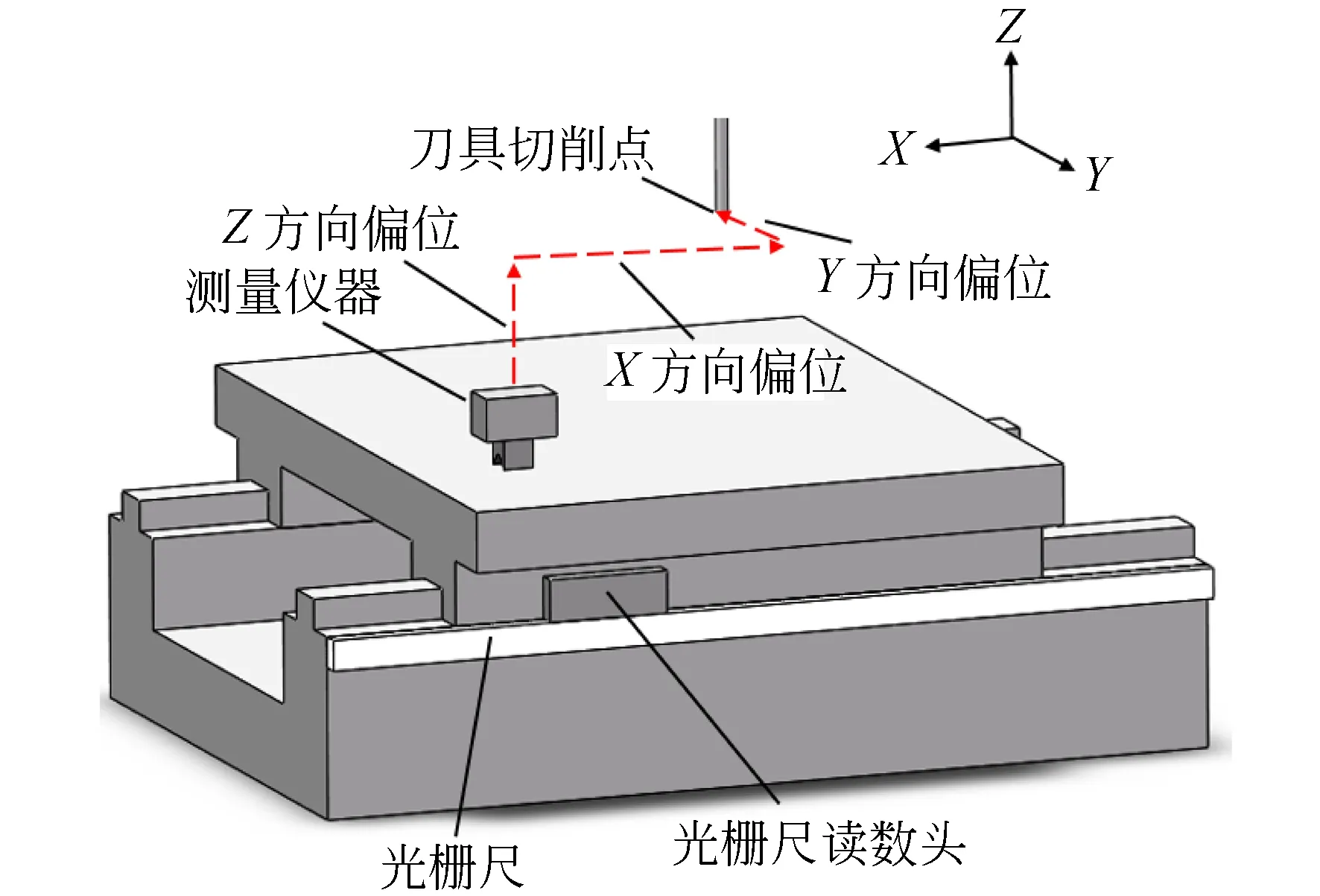
图3 误差测量点与刀具切削点偏位Fig.3 Offset between measuring point and cutting point of tool

但是在使用多自由度测量仪器测量机床运动轴几何误差时，在空间中刀具切削点和误差测量点的位置并不重合，两点间的偏位如图3所示。此时带入模型的几何误差在理论上由两部分组成：仪器测量得到的误差以及导轨角度误差在刀具切削点和几何误差测量点间的空间偏位作用下产生的阿贝误差。然而，现阶段在将几何误差带入补偿模型时，两点间空间偏位所造成的这部分误差项并没有被考虑，这就使得在使用HTM模型进行误差补偿时补偿精度受到制约。

3 阿贝原则在机床空间误差分析中的应用

3.1 空间误差传递

阿贝原则是测量仪器设计的指导性原则，指测量轴线必须与基准轴线共线，否者会在测量结果中引入阿贝误差[23]。这一原则也可被借鉴用来分析三轴机床的几何误差传递[19]。

在加工时，由于运动轴定位误差的存在，刀具切削点的真实位置与理想位置不重合，影响机床的加工精度。在以光栅尺为位置控制单元的机床上，运动轴的位置是靠光栅尺实时反馈得到的，所以将光栅尺的位置作为基准轴线。在加工时，刀具切削点与光栅尺不在同一轴线上，在空间上存在阿贝偏位，且在加工过程中运动轴存在运动姿态角度误差，所以会在刀具切削点处引入阿贝误差。刀具切削点的真实位置误差是由光栅尺处的定位误差和角度误差与阿贝偏位所引起的阿贝误差共同组成。

假设刀具切削点与X轴光栅尺在Z方向的偏位为Lz(x)，X轴在运动时的俯仰角误差为εy(x)，所以由X轴俯仰角误差在刀具切削点引起的X方向阿贝误差为：εy(x)×Lz(x)，如图4所示。

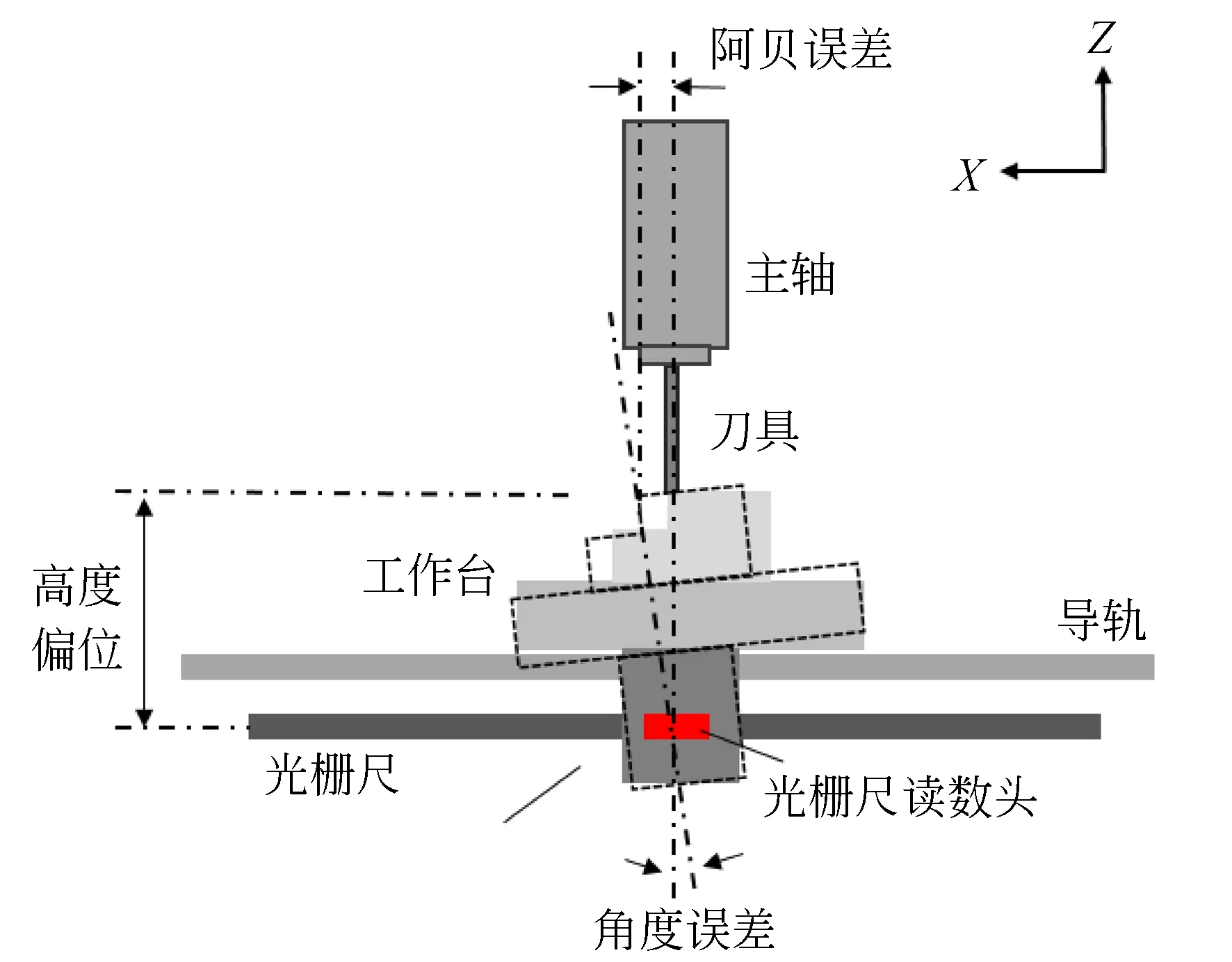
图4 阿贝偏位引入阿贝误差Fig.4 Abbe offset introduces Abbe error

实际加工中，刀具切削点与光栅尺读数头在空间中有3个方向的偏位，如图5所示，运动轴的偏摆角误差也会在刀具切削点处引入阿贝误差。所以刀具切削点处由X轴引入的X方向的几何误差应由三部分组成：光栅尺处的基准定位误差、俯仰角误差引入的阿贝误差以及偏摆角误差引入的阿贝误差，计算公式为：

δxt(x)=δxα(x)+εy(x)Lz(x)-εz(x)Ly(x)，

(4)

其中：δxα代表X轴光栅尺读数头处的基准定位误差，δxt代表刀具切削点处X方向的几何误差，Lz(x),Ly(x)分别为X轴光栅尺读数头与刀具切削点之间的Z向和Y向的偏位。

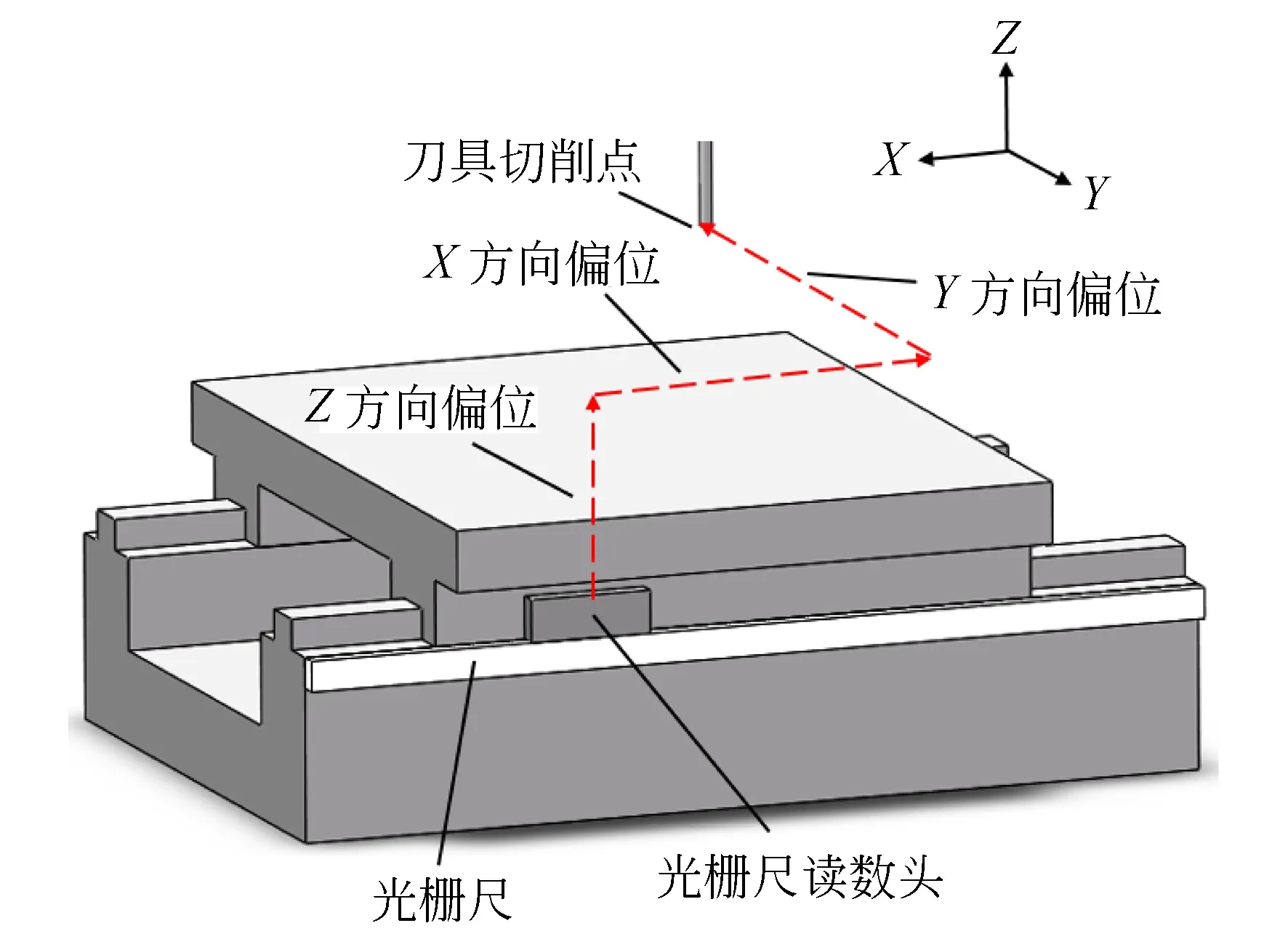
图5 刀具切削点与光栅尺读数头间偏位Fig.5 Offset between cutting point and reading head

3.2 阿贝原则的验证

为验证上述理论推导的准确性，在机床X轴上进行实验验证。首先，使用雷尼绍公司XM-60型多自由度测量仪器(精度：±0.5×10-6，分辨力：1 nm，测量范围：0～4 m)在距光栅尺水平偏位0 mm,竖直偏位分别为250，430和550 mm位置测量X轴的定位误差和俯仰角误差。定位误差测量示意图和仪器现场架设如图6所示。

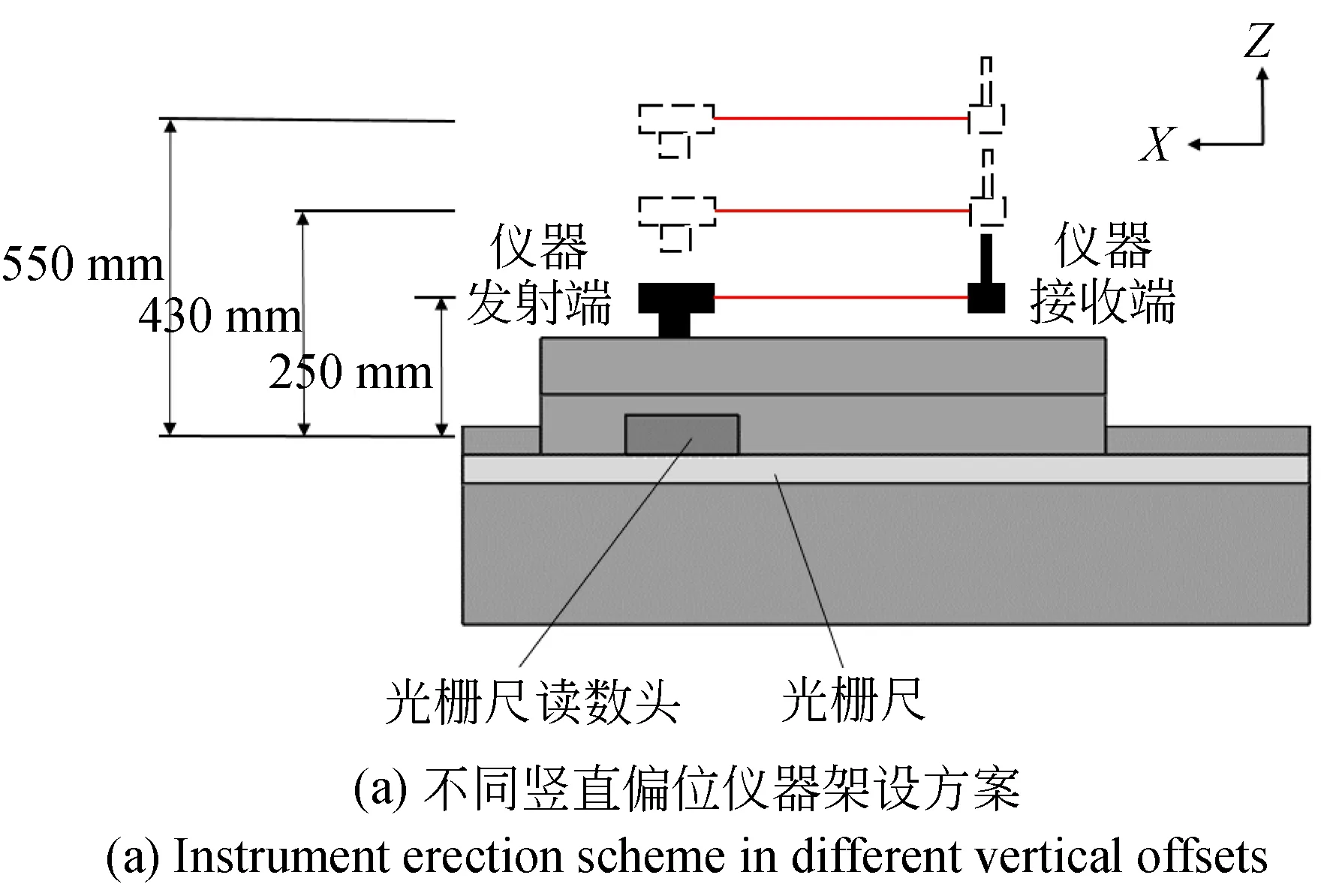
图6 不同竖直偏位仪器架设方案及现场安装图Fig.6 Instrument erection scheme and installation in different vertical offsets

在3个不同竖直偏位测量的俯仰角误差如图7所示。由于3个测量位置的水平偏位都为0，故偏摆角误差对于定位误差的测量结果没有影响，所以依照前述，在不同竖直偏位测量得到的定位误差由两部分组成：相同的基准定位误差和由于不同阿贝偏位所产生的阿贝误差。误差测量点处的定位误差值与光栅尺读数头处的定位误差值满足如下公式：

δxm(x)=δxα(x)+εy(x)Lmz(x)，

(5)

其中：δxα代表X轴光栅尺读数头处的基准定位误差，δxm代表定位误差测量点测量得到的定位误差值，Lmz(x)为X轴光栅尺读数头与误差测量点之间的Z方向偏位值。

通过公式(5)补偿不同高度测量点处包含的阿贝误差后，可得到光栅尺读数头处的基准定位误差，计算结果如图8所示。结果表明，3个不同高度的定位误差中包含相同趋势的基准定位误差，且相互间的差值基本保持在2 μm内，符合理论推导。

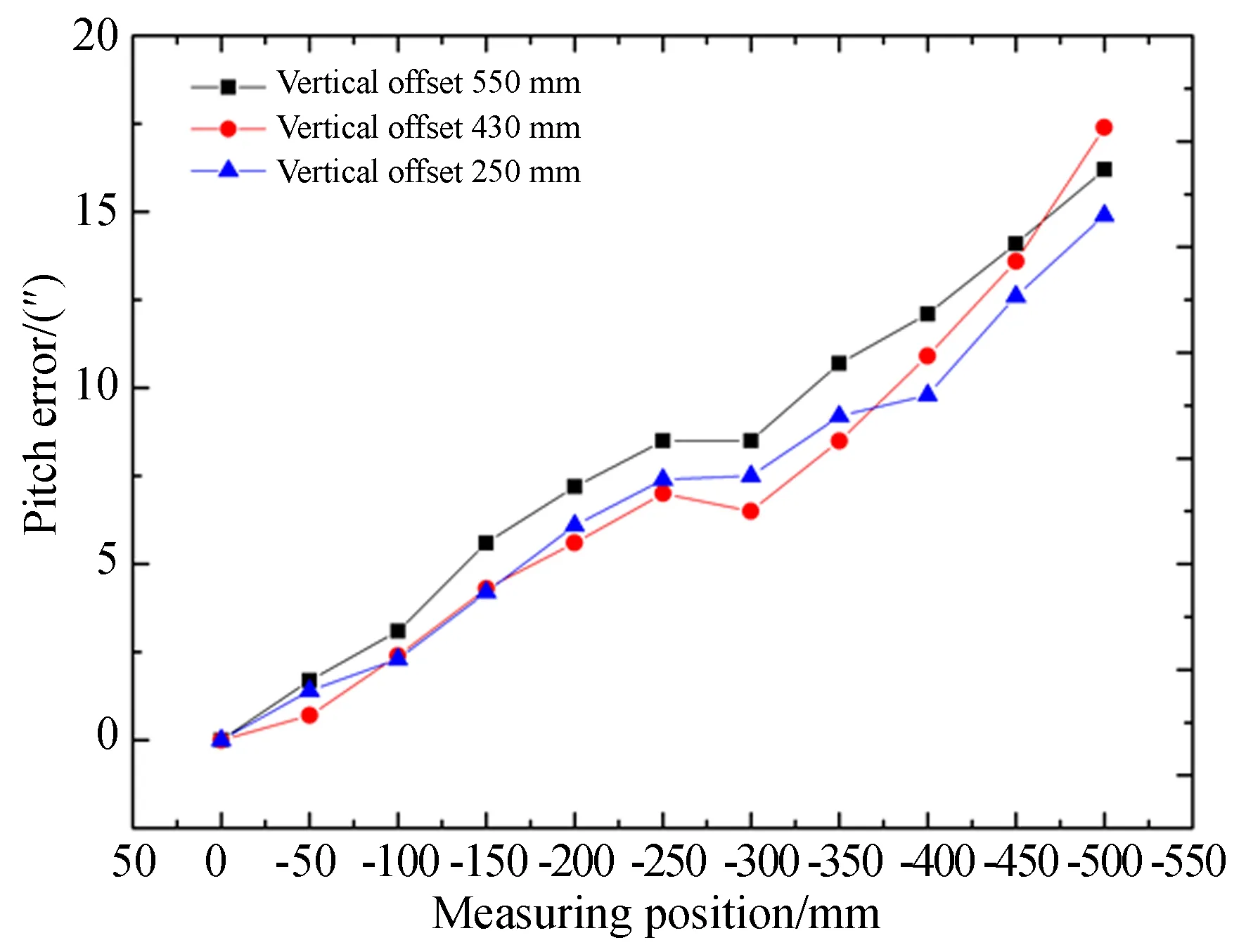
图7 不同竖直偏位测得俯仰角误差Fig.7 Pitch angle errors measured in different vertical offsets

图8 不同竖直偏位定位误差比对Fig.8 Alignment of positioning errors in different vertical offsets

除了俯仰角误差外，当测量轴线与基准轴线存在水平方向偏位时，导轨偏摆角误差也会在定位误差的测量结果中引入阿贝误差。使用雷尼绍公司XM-60型多自由度测量仪器在距光栅尺竖直偏位250 mm，水平偏位分别为0 mm和290 mm的位置测量X轴定位误差和偏摆角误差，定位误差测量示意图和仪器现场架设如图9所示。

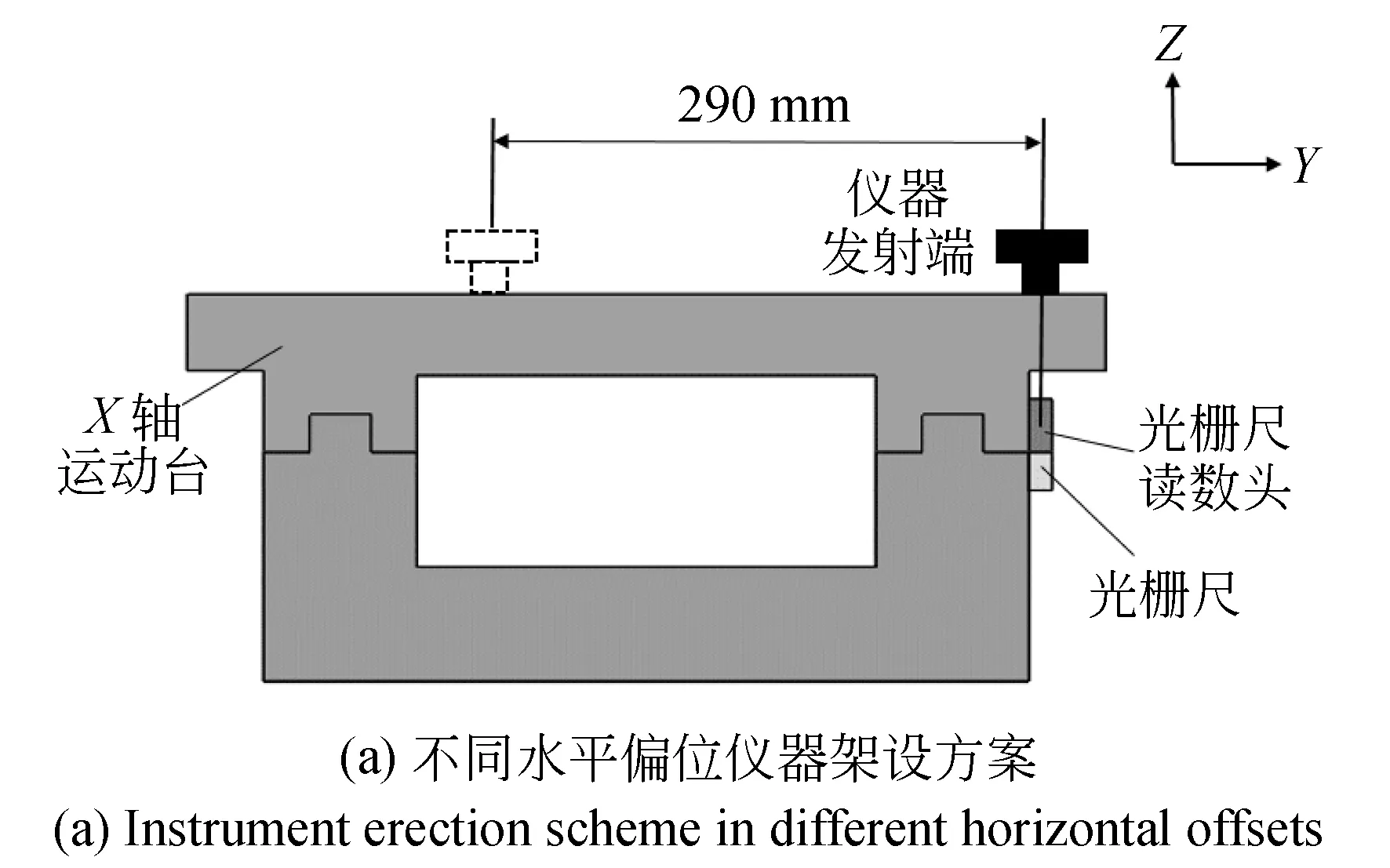
图9 不同水平偏位仪器架设方案及现场安装图Fig.9 Instrument erection scheme and installation in different horizontal offsets

当两个测量位置相对于光栅尺读数头的竖直偏位相同且水平偏位不同时，可认为是偏摆角误差在两点间定位误差中引入了阿贝误差。即290 mm处测量得到的定位误差是由0 mm处测量得到的定位误差和偏摆角引入的阿贝误差组成。两点间定位误差的计算公式如下：

δx290(x)=δx0(x)-εz(x)Lmy(x)，

(6)

式中：δx0,δx290分别代表在相对X轴光栅尺读数头水平偏位0，290 mm测得的定位误差，Lmy(x)为两误差测量点间的水平偏位。将290 mm水平偏位处测得的偏摆角误差(图10)带入公式(6)中可以计算得出0 mm处的“基准”定位误差，并将之与水平偏位0 mm处实际测得的定位误差进行比较，结果如图11所示，两者差值在1.3 μm内，符合理论推导。

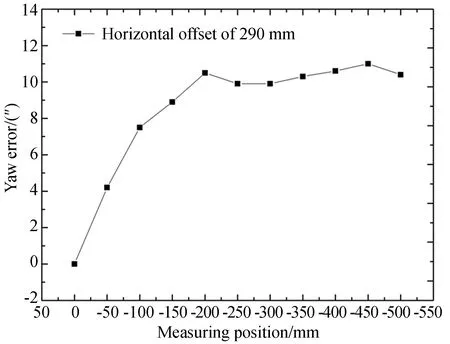
图10 水平偏位290 mm处测得的偏摆角误差Fig.10 Yaw angle errors measured in horizontal offset of 290 mm

图11 不同水平偏位定位误差比对Fig.11 Alignment of positioning errors in different horizontal offsets

由于机床结构的特殊性，在加工过程中，运动轴的定位误差在传递到刀具切削点时会引入角度误差造成的阿贝误差，具体计算如公式(4)所述。在使用HTM法进行补偿时，有一部分阿贝误差未被考虑，这是影响其补偿的主要原因。所以，基于阿贝原则和空间误差传递机理针对HTM补偿模型存在的不足进行优化，以达到提高补偿精度的效果就显得很有意义。

4 基于阿贝原则优化补偿模型

4.1 测量误差转换

误差测量是补偿的前提，由于使用便捷、测量效率高，多自由度误差测量仪器被越来越多地应用于机床几何误差量的测量中。测量时，仪器多架设于机床工作台上，这就使得误差测量点与刀具切削点存在偏位，且在进行多次重复测量时，安装人员很难保证仪器在工作台上的架设位置不变。根据前述理论，仪器在不同的安装位置测得的定位误差值由于阿贝误差的影响会产生变化，误差测量点与刀具切削点的空间偏位也会发生变化。如果每次测量都记录仪器位置，并针对测量点与切削点的偏位信息进行补偿，就会加大补偿工作量，使得补偿流程变得非常繁琐，同时也不利于补偿的重复实现。所以，为提高补偿精度以及不增加补偿流程的复杂度，现对HTM法以阿贝原则为基础进行优化。

由分析可知，虽然不同测量位置得到的定位误差不同，但其中包含的光栅尺读数头处的基准定位误差都是相同的，所以可以依照公式(4)把仪器测量得到的定位误差转换为光栅尺读数头处的基准定位误差，然后再带入补偿模型。在基于多体系体理论推导误差模型时，运动轴6项几何误差必须位于同一位置，所以在对定位误差进行转换时，也基于布莱恩原则[24]将直线度误差由测量点转换到光栅尺读数头处。由于运动轴可被视为刚体，角度误差不需转换。X轴定位误差和直线度误差转换公式如下：

δxm(x)=δxα(x)+εy(x)Lmz(x)-εz(x)Lmy(x)，

(7)

δym(x)=δyα(x)-εx(x)Lmz(x)+εz(x)Lmx(x)，

(8)

δzm(x)=δzα(x)+εx(x)Lmy(x)-εy(x)Lmx(x)，

(9)

其中：δxα,δyα,δzα分别代表光栅尺读数头处x,y,z方向的误差值，δxm，δym,δzm分别代表误差测量点测量得到的x,y,z方向的误差值，Lmx(x),Lmy(x),Lmz(x)分别代表X轴上几何误差测量点到光栅尺读数头处的X，Y，Z三个方向的偏位。

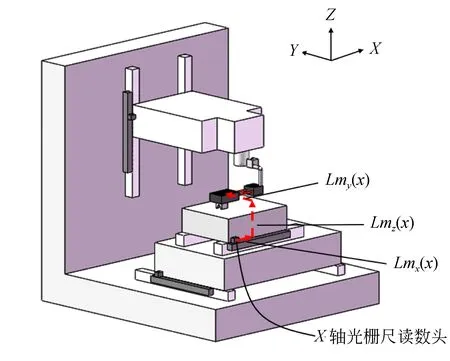
图12 X轴误差测量点与光栅尺读数头间偏位Fig.12 Offset between error measuring point and reading head on X-axis

4.2 误差模型优化

误差测量点与低序体坐标系原点重合是补偿的前提条件，所以现将机床运动轴固连坐标系设置在各轴光栅尺读数头处。将床身绝对坐标系的坐标原点设定为机床位于绝对零点时Y轴光栅尺读数头处，为保证补偿的准确性，在进行坐标转换时还要考虑机床位于绝对零点时各相对坐标系间的空间偏位，坐标系设置及坐标系间偏位如图13所示。此时的空间偏位信息也可用齐次坐标表示如表4。

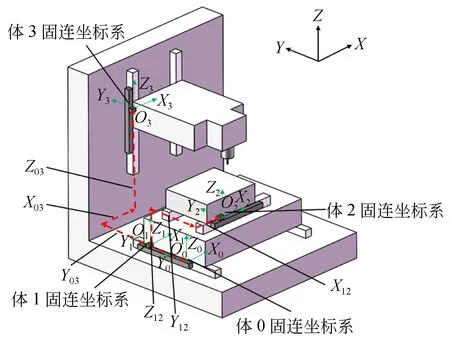
图13 优化后坐标系及坐标系间偏位Fig.13 Coordinate system and offset between coordinate systems after optimization

表4 相对坐标系间偏位表达式

Tab.4 Partial expression for relative coordinates

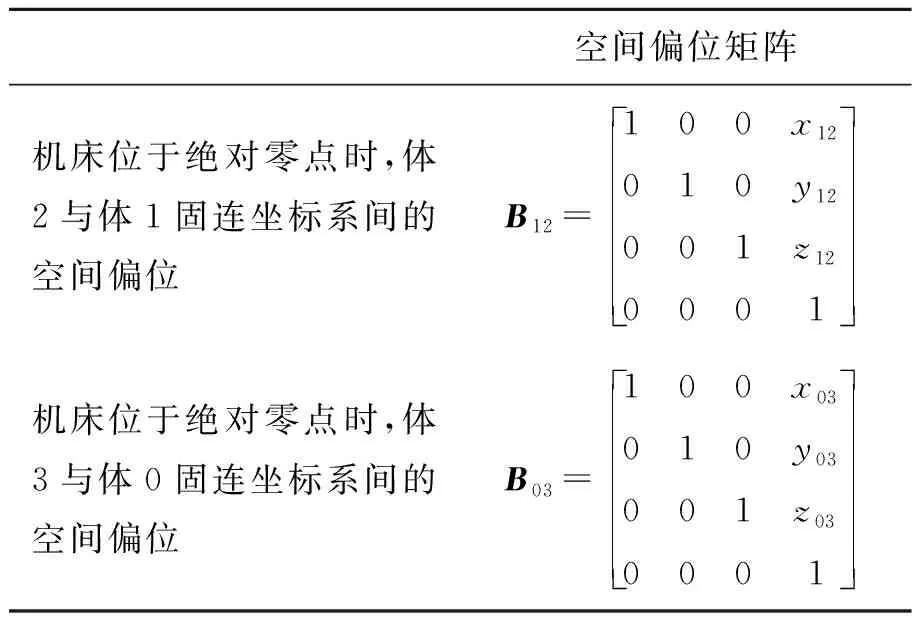
空间偏位矩阵机床位于绝对零点时,体2与体1固连坐标系间的空间偏位B12=100x12010y12001z120001机床位于绝对零点时,体3与体0固连坐标系间的空间偏位B03=100x03010y03001z030001

除了运动轴的几何误差外，各轴间的垂直度误差也会对空间误差产生影响。机床加工时，非基准轴在运动过程中会因为垂直度误差的存在而在基准轴上产生一个误差，如图14所示。

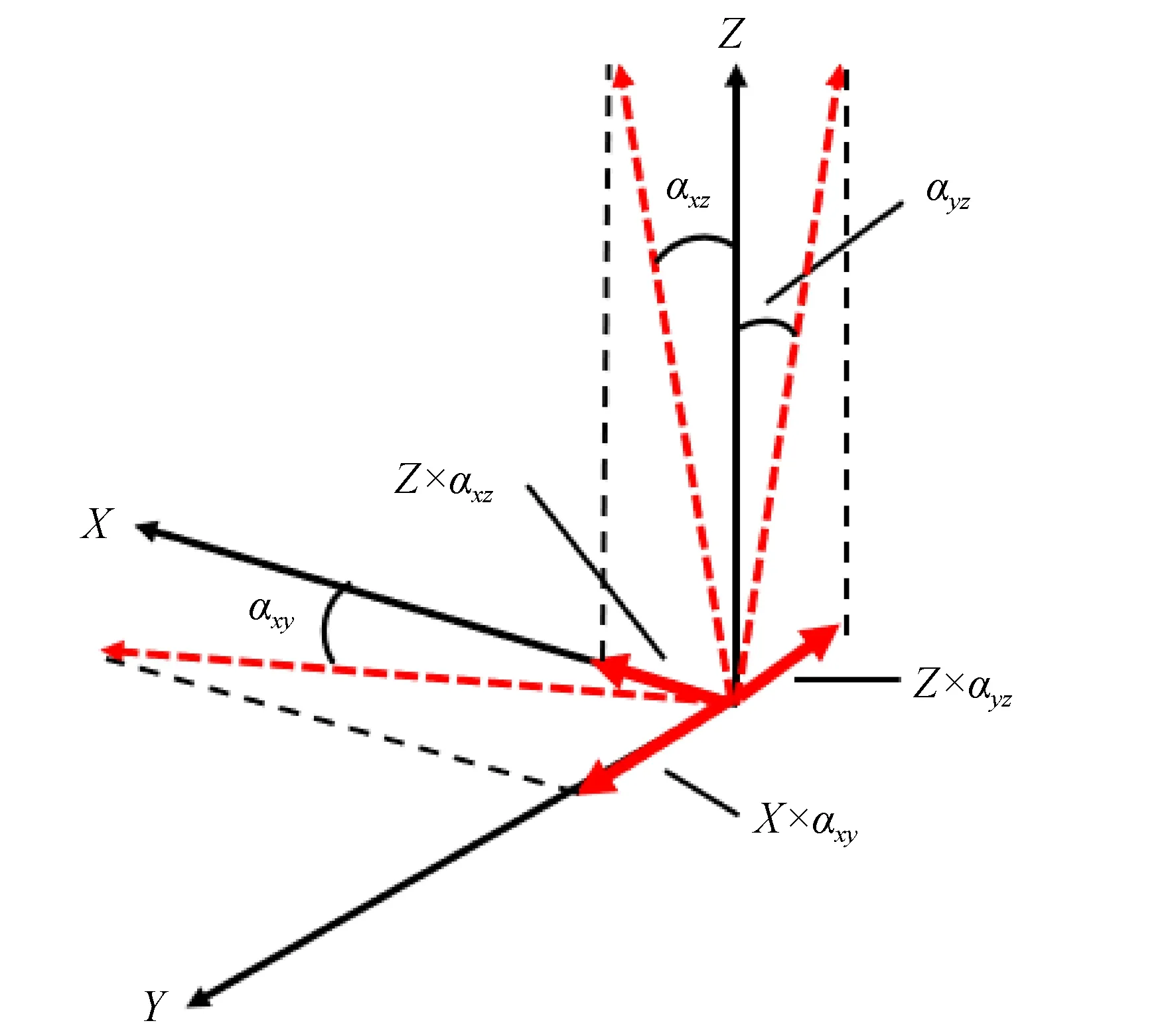
图14 垂直度误差对空间误差的影响Fig.14 Influence of verticality error on spatial errors

所以3个垂直度误差对于空间误差的影响可以按照齐次向量的样式写为：

C=(Zαxz,Xαxy-Zαyz,0,0).

(10)

基于阿贝原则优化后的空间误差算法如下：

Pactual-w=T01ΔT01B12T12ΔT12Pw，

(11)

Pactual-t=B03T03ΔT03Pt,

(12)

E=Pactual-t-Pactual-w+C.

(13)

针对误差补偿模型的优化主要有三点：首先，考虑了由于误差测量点与刀具切削点间偏位产生的误差对于空间误差的影响；然后，基于阿贝原则和多体系统理论规范了相邻低序体固连坐标系坐标原点的选取原则；最后，在模型中加入表示机床位于绝对零点时相邻低序体固连坐标系间空间偏位的特征矩阵，使得模型的计算过程更加合理。

5 实验与结果分析

以江山华科XHK715型三轴数控机床为实验对象，验证针对HTM补偿模型的优化是否有效。

5.1 几何误差测量

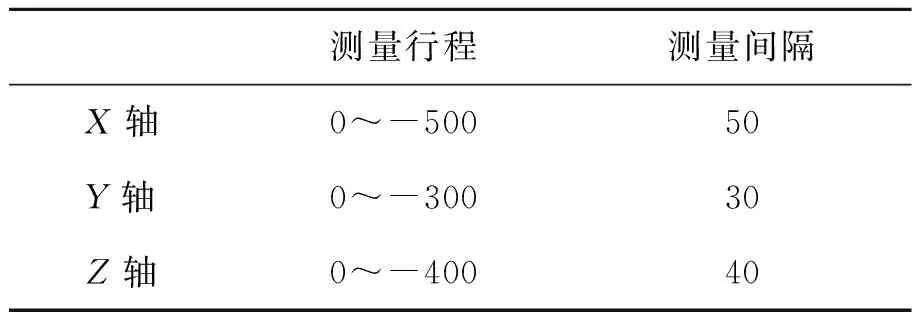
首先，使用雷尼绍公司XM-60型多自由度测量仪器分别测量机床X,Y,Z运动轴的6项几何误差，测量行程及测量间隔如表5所示。反复测量5次[19]，以5次测量的平均值作为导轨的几何误差。

表5 各轴测量行程及测量间隔

Tab.5 Measuring stroke and interval of each axis (mm)

测量行程测量间隔X轴0～-50050Y轴0～-30030Z轴0～-40040

机床各轴的测量现场以及测量结果分别如图15和图16所示。

图15 测量X，Y，Z轴几何误差仪器安装示意图Fig.15 Instrument installation diagram for measurement of geometric errors of X, Y and Z axes

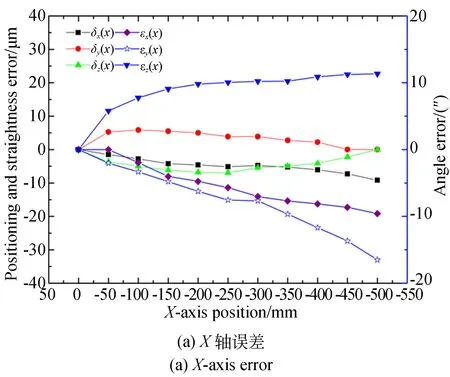
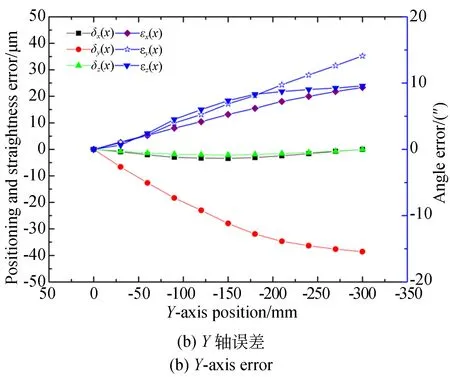
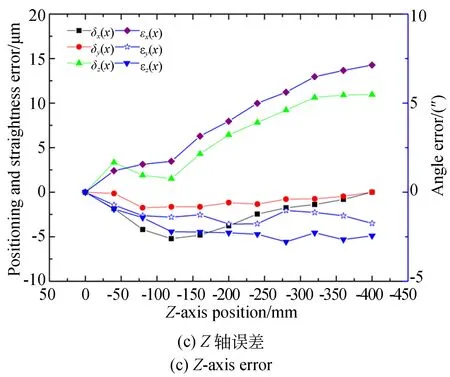
图16 X，Y，Z轴几何误差的测量结果Fig.16 Measurement results of X, Y and Z axial geometric errors

运动轴几何误差测量完成后，使用雷尼绍公司QC20-W型球杆仪(精度：±(0.7+0.3%L)μm，分辨力：0.1 μm，测量范围：±1 mm)测量机床的三项垂直度误差，测量结果如表6所示，仪器测量现场如图17所示。

表6 垂直度误差

图17 测量垂直度误差仪器安装示意图Fig.17 Instrument installation diagram for measurement of perpendicularity errors

5.2 模型准确性验证

根据ISO标准，可以通过检测机床运动空间体对角线定位误差估算机床的空间性能[25]。以此为基础，提出一种补偿模型验证方法。将补偿模型计算得到的空间误差映射到体对角线上，得到机床体对角线预测定位误差，再将预测定位误差与使用干涉仪实际测得的体对角线定位误差比对，反映补偿模型的补偿精度高低。

使用API公司XD激光干涉仪(精度：0.5×10-6，分辨力：0.02 μm，测量范围：40 m)测量机床500 mm(X)×400 mm(Y)×300 mm(Z)空间体对角线的定位误差，如图18所示。

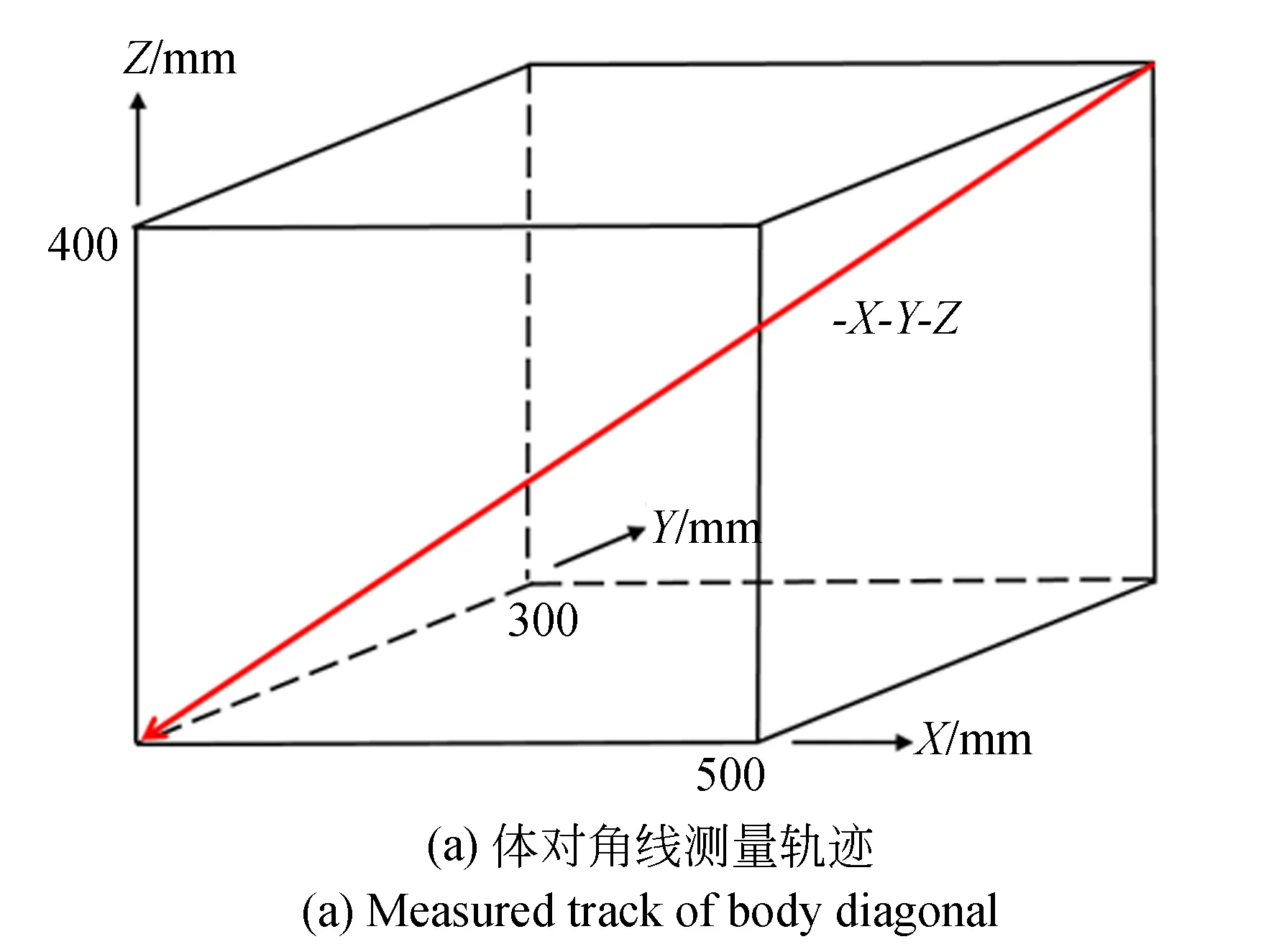
图18 体对角线测量轨迹及仪器安装示意图Fig.18 Measured track and instrument installation diagram of body diagonal

将测量得到的21项几何误差分别带入优化前和优化后的补偿模型生成空间误差补偿值，拟合得到体对角线预测定位误差，将实际测得的定位误差与预测误差进行比较，结果如图19所示。测量所得的体对角线最的大定位误差为41.15 μm，两个补偿模型拟合出的体对角线的最大定位误差分别为47.51 μm和42.61 μm，且拟合得到的体对角线定位误差与由干涉仪实际测量得到的定位误差的变化趋势基本相同。

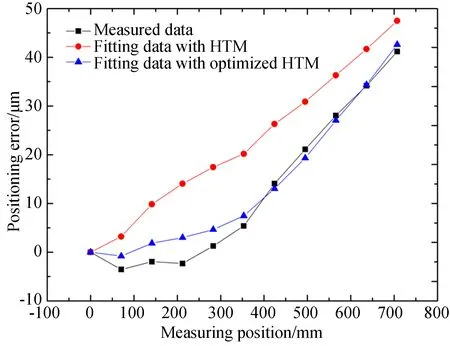
图19 拟合体对角线定位误差比对Fig.19 Comparison of fitting body diagonal positioning errors

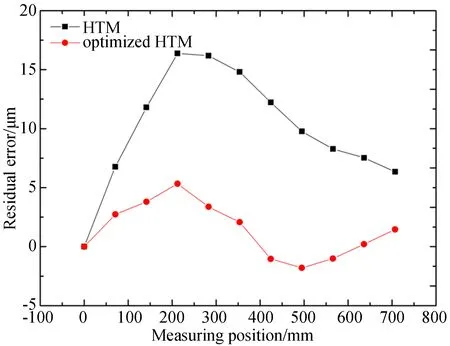
图20 体对角线定位误差补偿残差比对Fig.20 Comparison of compensation residual of body diagonal positioning errors

使用模型预测误差对测量所得的定位误差进行补偿，补偿后残差如图20所示。结果表明：未优化模型补偿后的最大残差为16.37 μm，优化后模型补偿后的最大残差为5.32 μm，优化模型的补偿率为87.07%，未优化模型的补偿率为60.22%，优化后补偿模型的补偿效果更好。

6 结 论

本文基于阿贝原则对HTM误差补偿模型进行了优化，提出符合多体系统理论的坐标系选取原则，使得补偿模型的理论推导更加合理。首先推导出HTM补偿模型，并指出使用多自由度测量仪器配合HTM补偿模型进行空间误差补偿时，误差测量点与补偿点不重合会导致补偿精度的降低。随后分析了三轴机床空间误差的传递机理，基于阿贝原则对HTM补偿模型进行了优化。实验表明，优化后的补偿模型可将机床空间体对角线的定位误差由41.15 μm补偿至5.32 μm，补偿率为87.07%；相比于传统HTM补偿模型，补偿率提高了26.85%，对于机床空间误差具有更好的补偿效果。