孤立波作用下植物带消浪效果影响因素分析
龚尚鹏,陈 杰, 2, 3,蒋昌波, 2, 4,童忠武
(1. 长沙理工大学 水利工程学院,湖南 长沙 410114; 2. 水沙科学与水灾害防治湖南省重点实验室,湖南 长沙 410114; 3. 洞庭湖水环境治理与生态修复湖南省重点实验室,湖南 长沙 410114; 4. 湖南省环境保护河湖疏浚污染控制工程技术中心,湖南 长沙 410114)
近岸植物能有效削减波能,海浪在近岸植物带衰减的影响因素一直是消浪研究重点关注的问题[1]。国内外针对植物带消浪影响因素进行了大量的试验研究工作。陈杰等[2]通过试验数据定性分析影响因素与消浪效果之间的变化规律,但未明确指出各影响因素权重。章家昌[3]、白玉川等[4]、何飞等[5]结合物理模型试验,采用传统的量纲分析方法,通过拟合得到影响因素与消浪效果之间的半理论半经验公式。但传统的回归拟合方法限定了公式结构,复杂的植物构造和多元数据结构使得传统研究方法难以得到有效的应用,可能会对衰减规律的理解产生误解。
遗传编程和人工神经网络等方法被广泛应用于因素分析中,可为海洋工程提供新的研究思路和手段。如Keijzer等[6]利用遗传编程方法来确定植物阻力方程,将理论研究方法与基于遗传编程数据驱动结果进行比较,结果表明遗传编程能够得到更为简洁和准确的关系;夏元友等[7]指出使用人工神经网络方法进行边坡稳定性影响因素敏感性分析不仅可靠,而且方便简单。
因此,本文引入遗传编程方法和人工神经网络方法对孤立波作用下植物消浪的物理模型试验数据进行分析,探究植物消浪影响因素的作用,得到植物消波计算公式,对各影响因素敏感度进行排序。旨在解决传统方法的不足,提供一种更为有效和准确的物理解释和预测方法,进一步揭示植物消浪特性与水动力因素和植物因素的内在联系。
1 植物带透射系数的定义及影响因素研究
植物消浪效果受水动力和植物因素共同作用,水动力因素包括水深[2]、入射波高[2,5]、波长[3]、周期[8]等;植物因素包括植被高度[9]、植物带长度[10]、植物带密度[2]、分布方式[11]以及植被种类[12]等。陈杰等[1]相关研究指出,海啸波水动力因素主要包括水深h、周期T、入射波高H和波长L。植物因素主要包括植物高度hv、植物带宽度B和体积分数φ。
在植物消浪过程中,植物带前后的波高变化受到广泛关注,所以采用透射系数[2]来描述植物消浪效果。透射系数的定义为波浪透过植物带时,植物带后的透射波高与植物带前的入射波高的比值,透射系数Kt越大,表明植物带的消浪效果越差。

(1)
式中:Kt为透射系数,Ht为透射波高,Hi为入射波高。
因此,植物带的透射系数可用以下函数表示:
Kt=f(h,H,L,hv,B,φ)
(2)
参考Huang等[13]的实验室孤立波波长计算:

(3)
体积分数[2]采用下式计算:

(4)
式中:Vs为淹没部分的植物体积,V为水面以下整个分布区域体积,N为植物株数,Ss为单株植物横截面积,S为分布区域面积。
为了排除各因素的单位限制,同时数据无量纲化有助于遗传编程得到更优的结果,将关系式中的影响因素进行无量纲变化可以得到:

(5)
式中:RH=H/h为相对波高,可综合反映孤立波水动力因素的影响;RB=B/L为模型相对宽度,反映了在水流方向上植物长度与波长的比值,可表征植物带相对宽度的影响;α=hv/h为模型相对高度,可表征植物带高度的影响;φ为体积分数,可表征植物带密度和横截面积的影响。
2 试验概述
试验在波浪水槽进行,波浪水槽尺寸为40.0 m×0.5 m×0.8 m(长×宽×高)。水槽一端配有推板式造波机,植物模型放置于水槽中段,另一端配有网状消波设施。共设置6个WG-50型浪高仪(G1-G6)测量浪高沿程变化,G3和G6分别用来采集入射波高和透射波高,布置方式如图1所示。

图1 试验布置Fig. 1 Experimental setup
植物树根和树叶空间结构复杂,仅在一定条件下对消浪效果产生显著影响。为便于研究,Augustin等[14]倾向于忽略植物根部和冠部结构特征,将植物简化为垂直圆柱。本试验模型设计结合Maza等[15]对红树林海岸相关树种的调查资料,参考黄本胜等[16]研究,同时考虑试验室场地和器材条件限制,采用PVC圆管来模拟刚性植物,几何比尺采用1∶20,模拟的实际树干直径为0.2 m。PVC圆管刚性与红树林树干相似,弹性模量E为2 900~3 000 MPa,且制作简单。PVC塑料圆管粗细均匀,圆管直径为0.01 m,高度为0.5 m。
红树林的分布方式杂乱多样且与地形地貌有关。为反映多种体积分数和分布方式的影响,试验共采用10种模型方案。植物分布方式见图2。为插置植物模型,采用长宽高分别为0.5 m、0.48 m、0.016 m的模型底板固定圆管,圆管在图中以黑色圆点表示,在底板上穿孔,孔间距L为0.025 m。

图2 植物模型分布方式俯视图Fig. 2 Top view of vegetation arrangements
试验采用孤立波,根据试验比尺和仪器条件测试10种不同模型,每种模型15种波浪条件,共150组工况。各模型植物分布方式及试验工况如表1所示。

表1 各模型植物分布方式参数Tab. 1 Vegetation distribution pattern parameters of each model
试验时,先打开造波机进行预热,随后打开数据采集系统,检查并确保浪高仪性能良好,然后调整水槽内水位至设计水位,待水面平静后控制造波机造波,同时采集浪高仪数据并保存,试验采集时间从造波机造波开始,至整个孤立波通过浪高仪后结束,采样频率为128 Hz,浪高仪最小测量时间1.5 μs,误差为0.4%,为保证数据的准确性,每组工况均至少一次重复性试验。
3 试验数据结果分析
3.1 遗传编程方法
3.1.1 遗传编程方法基本原理
遗传编程适用于归纳数学模型,与传统非线性拟合相比能更有效地理解数据内蕴藏的规律,不需要假定潜在关系的函数形式,能够自动揭示数据集中隐藏关系并生成因变量和自变量之间的函数关系式[17]。Giustolisi[18]基于物理模型试验数据,指出使用遗传编程方法得到的渠道谢才系数计算公式与传统公式相比更加准确。因此选用遗传编程方法来得到植物消浪效果的计算公式,并进行敏感性分析。
遗传编程是一种基于函数和终端解析树的高效弱搜索算法,一般使用树型结构或字符串来表示个体,分层树结构的叶节点是问题的原始变量,中间结点是组合这些原始变量的函数。借鉴生物进化论的自然选择和遗传学机制,在进化过程中,树的深度、形状都在不断地改变,根据个体的适应度来选择个体。以相应符号的方程形式对物理和概念过程进行更精细的表示。每个方程都可以看作是符号的集合,符号构成了对象、过程或事件的模型。图3是方程Kt=0.662+0.010 7/φ-0.632α的树状结构,包括函数符与终止符两部分,其中函数符集合为{+,-,×,/},终止符集合为{α,φ,0.662,0.010 7,0.632}。

图3 遗传编程个体Fig. 3 Individuals based on genetic programming
3.1.2 遗传编程方法分析结果
利用遗传编程方法对试验数据进行分析,将透射系数Kt、相对波高RH、模型相对宽度RB、模型相对高度α、体积分数φ作为数据输入,其中透射系数为因变量,其余为自变量。确定运算符号为+、-、×、/、sin、cos,运算得到不同复杂度下的最优方程,如表2所示。
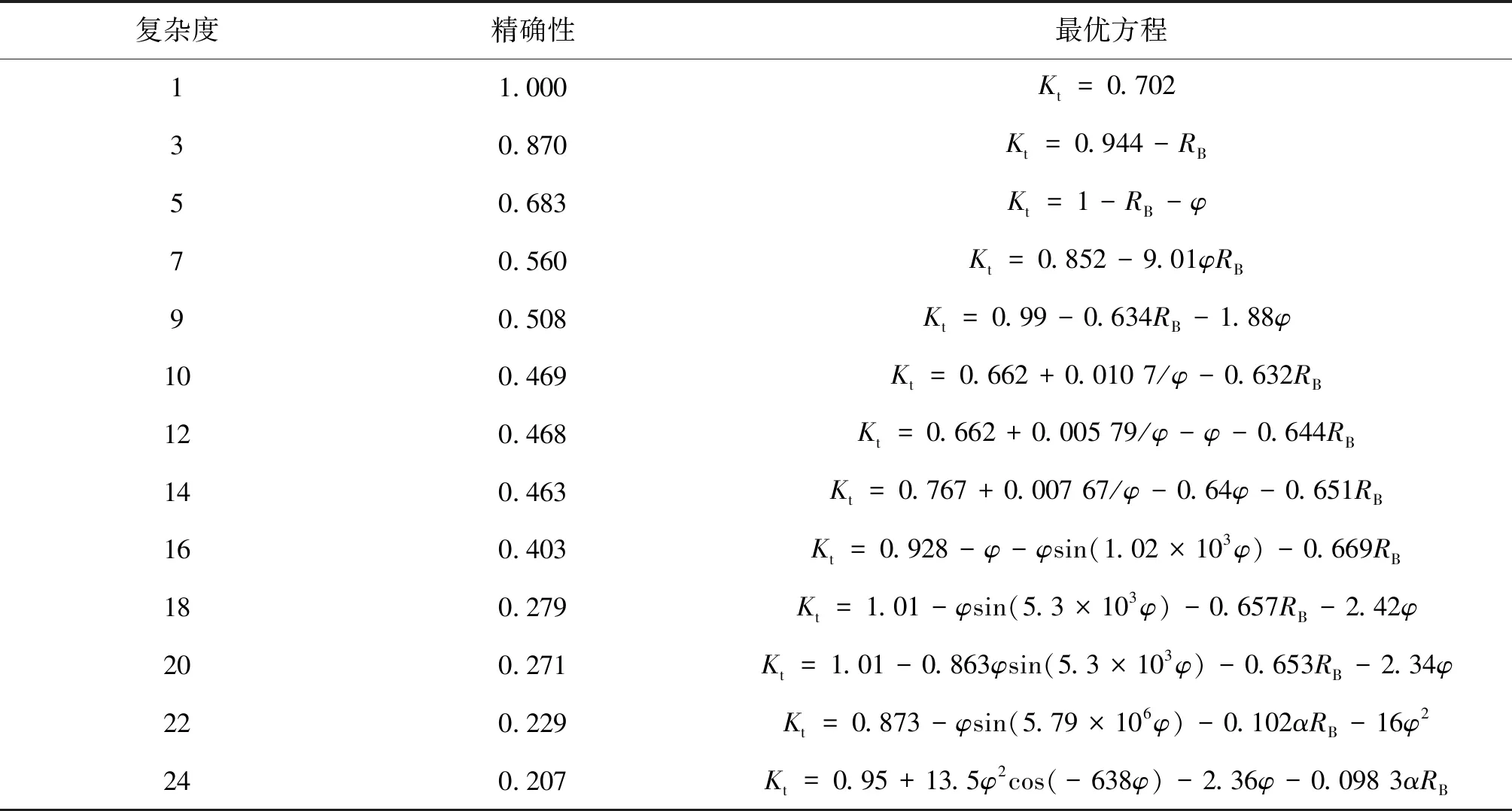
表2 最优方程拟合结果Tab. 2 Fitting result of the optimal equation
随着分析时间增长,可得到复杂度高达134的最优方程。表2中省略了复杂度大于24的最优方程,尽管复杂度越大,得到的最优方程拟合度越高。但认为此时的公式结构过于复杂,遗传编程盲目地将解析树与数据相匹配,导出函数关系缺乏物理意义。从表2可以发现,各无量纲因素在某一复杂度的最优公式中可能出现或不出现,也可能出现一次或多次。体积分数φ出现次数最多,模型相对宽度RB和模型相对高度α出现相对较少,而相对波高RH出现次数最少。用某一无量纲因素在所有最优方程中出现的次数和出现该因素的最优方程数两个指标来衡量该因素在遗传编程结果中的表现。如图4所示,为直观体现各因素表现情况,将各个因素的两项指标绘制成直方图。

图4 因素在方程中的表现Fig. 4 Performance of the factors in the equation

图5 10次拟合各因素指标均值Fig. 5 Mean values of the indicators of each factor in the 10 times fitting
由于使用遗传编程方法求解存在随机性,每次拟合结果的最优方程存在差异,各无量纲因素在方程中的表现也随之发生改变。为了避免单次拟合结果引起的判断误差,统计重复10次拟合结果中出现各因素在所有最优方程中出现次数以及出现该因素的最优方程数并求得平均值,绘制成图5。
根据图4和图5可知,各因素出现次数存在明显差异,其中体积分数φ在10次拟合结果中出现次数最多,其次是模型相对高度α、模型相对宽度RB和相对波高RH。拟合结果表明,体积分数与透射系数之间关系紧密,体积分数对植物消浪的效果影响最大。
3.2 人工神经网络方法
3.2.1 人工神经网络方法基本原理
人工神经网络是一种受大脑中生物神经网络所启发,但不完全相同的非线性运算模型。这类系统通过考虑实例“学习”执行任务,通常不需要编写任何特定于任务的规则,给定训练网络足够的复杂度,神经网络可以表示任意非线性函数。网络由许多相互连接的节点(神经元)组成,它们被安排成输入、隐藏和输出三个基本层,在神经元的传递间赋予相关权重,通过使用算法不断调整这些权重,从而得到最小预测误差并给出预测精度[19],被广泛应用于参数的敏感性分析之中[7]。与遗传编程不同的是,神经网络无法得到明确的函数关系式。
如图6所示,本文神经网络采用3层结构,将相对波高、模型相对高度、模型相对宽度和体积分数作为输入数据,透射系数作为输出数据进行分析。采用极差法将数据标准化处理,训练样本数量为100组,占总数据量的66.7%,测试样本数量50组,占总数据量的33.3%,数据全部有效。
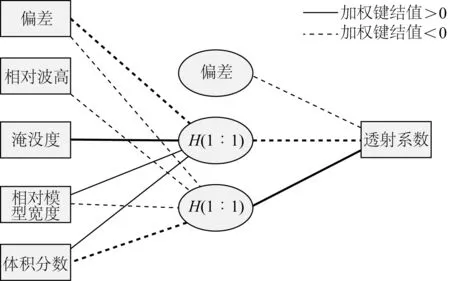
图6 网络图Fig. 6 Network diagram
3.2.2 人工神经网络分析结果
使用SPSS软件中神经网络分析方法中多层感知器对试验数据进行分析,训练集平方和错误11.182,相对误差0.226。测试集平方和错误6.763,相对误差0.231。分析结果如表3所示。
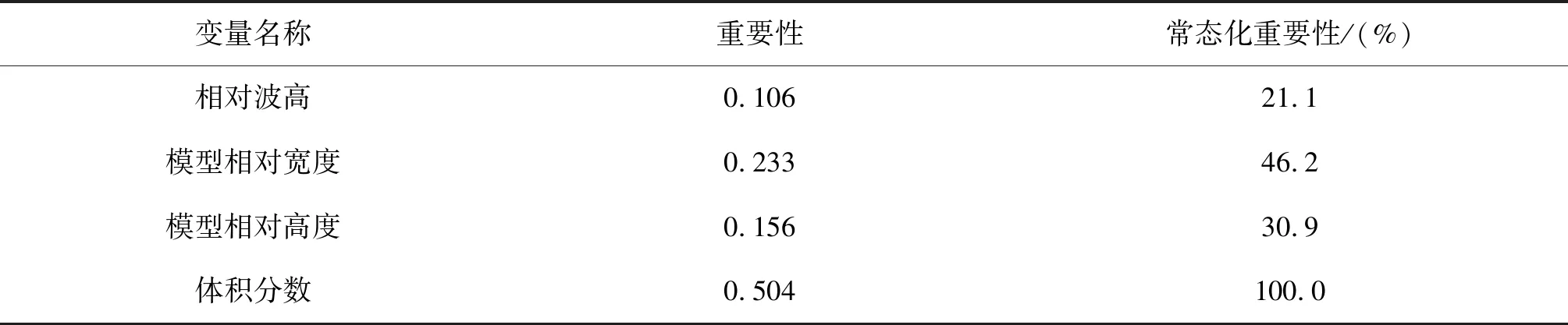
表3 自变量的重要性Tab. 3 Importance of the independent variables
由表3可知,体积分数对透射系数影响最大,其计算结果重要性值达到了0.504。模型相对宽度次之,模型相对高度和相对波高对透射系数影响相对较小。
3.3 结果对比分析与讨论
3.3.1 遗传编程方法与非线性回归拟合对比
为探究遗传编程方法与白玉川等[4]采用的非线性回归方法的差异,基于本文模型M1~M10的试验数据,选用幂函数的形式,以透射系数为因变量,相对波高、模型相对宽度、模型相对高度和体积分数为自变量进行多元非线性回归拟合。结果如式(6)所示。

(6)
分别将试验中的四个无量纲参数代入遗传编程结果(表2中复杂度为24的最优方程式)和多元非线性回归拟合结果(式6),得到两种方法的预测值,预测值与实测值对比见图7。值得说明的是遗传编程结果中复杂度过低和复杂度过高的最优方程均缺乏实际意义,如表2中当复杂度小于20时,拟合的结果受数据的影响较大,模型相对高度α没有在最优公式中出现。当复杂度达到20左右时,其最优方程的决定系数一般可达到0.9以上,复杂度越大表明公式结构越复杂,而决定系数提升较小,实际意义不大。
图7(a)为非线性回归拟合结果的实测值与预测值的关系,其决定系数R2为0.75,部分数据点与拟合线偏离较远,说明采用非线性回归拟合得到的公式对实测值的拟合程度较差。图7(b)为遗传编程拟合结果的实测值与预测值的关系,其决定系数R2高达0.95,相较于(a),数据点与拟合线更为贴近。对比分析结果表明,与传统的非线性回归拟合方法相比,遗传编程方法能够得到更准确的预测公式。
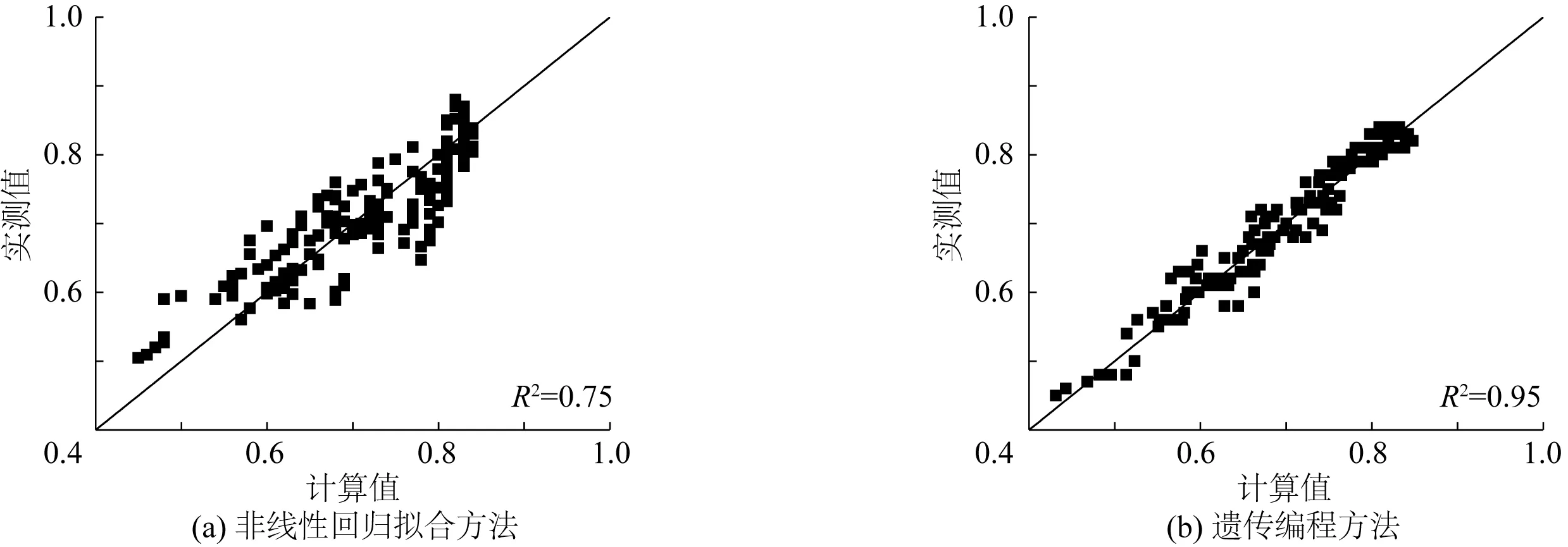
图7 遗传编程结果与非线性回归分析结果对比Fig. 7 Comparison between genetic programming and nonlinear regression analysis
3.3.2 遗传编程与人工神经网络敏感性分析结果对比与讨论
人工神经网络方法与遗传编程方法的敏感性分析结果均表明体积分数对植物消浪效果的影响明显占主导作用,模型相对宽度、相对高度和相对波高的影响相近,相对波高的影响较小。对于模型相对宽度和模型相对高度两种方法出现了不同的结果,认为原因可能是由于遗传编程的结果是随机产生的,从而导致每次拟合的最优方程表都不完全一致,使得到的统计结果存在一定误差。
各无量纲参数对植物消浪的效果有不同的表现。体积分数对植物消浪的影响最大,这与Mazda等[20]对越南三角洲的秋茄红树林开展的现场测量研究结果相同。体积分数反映单位体积植物带内植物对波浪水体阻水体积的大小,一定条件下,体积分数越大,植物带的消波效果越好[1, 14]。模型相对长度对植物消浪的影响较体积分数小,但也影响显著。Phuoc等[21]对越南南部Can Gio的红树林现场研究结果表明,波浪在红树林中的传播距离与消波效果显著相关。模型相对长度反映波长与植物带沿流向长度的比值,该比值大于1或小于1呈现出不同的消波效果[9]。模型相对高度综合考虑了植被高度与水深对消波效果的影响,同样,当模型相对高度大于1时,植物处于非淹没状态,此时植物的形状阻力是产生消波效果的主导,但模型相对高度小于1时,植物顶部出现剪切层,此时剪切和形状阻力都对消波效果产生影响[22]。相对波高表征水动力因素影响,在同水深情况下,波高越大,植物带的消波效果越好[2]。
4 结 语
植物消浪研究中产生的大量多元素、多尺度的试验数据使得传统研究方法难以得到有效应用。遗传编程方法有助于理解和建立新的公式,并对数据进行有效分析和预测,为解决植物消浪相关复杂问题提供新的思路和方法。研究选取与植物消浪影响效果密切相关的相对波高、模型相对宽度、模型相对高度、体积分数4个无量纲因素,采用透射系数大小衡量植物消浪效果。使用遗传编程、非线性回归拟合和神经网络3种分析方法对各因素进行了公式拟合与权重分析,发现体积分数对植物消浪的影响最大,模型相对宽度和模型相对高度次之,相对波高对植物消浪效果影响最小。研究结果对近岸植物消波护岸工程具有一定的指导意义。

