渗透数形结合思想是发展学生核心素养的重要举措

熊安竹 曹少燕

摘 要 在小学数学教学中，渗透数形结合思想是发展学生核心素养的重要举措。数学课程标准中提及的十大核心素均可以通过数形结合思想来实现。在具体的数学问题中，数形结合思想的运用是实现核心素养的承载者。

关键词 数形结合思想 核心素养

中图分类号：G622文献标识码：A

数学核心素养是数学学习者在学习数学或者学习数学的某一个领域所到达和形成的一种综合的能力，是在学习和实践当中最基础的能力之一。《义务教育数学课程标准》明确提出了几个核心素养，分别是：符合意识、数感、空间观念、几何直观、数据分析观念、运用能力、推理能力、模型思维、应用意识和创新意识。以上十大核心素的体现均可以通过数形结合思想来实现，在具体的数学问题中，数形结合思想的运用是实现核心素养的承载者。根据数形结合思想运用的不同作用，可以将十大核心素养合并为四大类来讨论。

1数形结合思想在发展学生符号意识、数感中的重要作用

符号意识和数感均由“形”直接转变过来，所以合并为一类。特别是低年级数学教学中，数字及数的认识部分以及估算等内容，数形结合思想的应用可以很好发展学生的符号意识和数感。如用简单的几个圆圈或者小竖线来代表复杂的物体，再将圆圈或小竖线转变为具体的数字，孩子们极易理解和接受。在教授加减法运算时的画一画就是典型的数形结合思想运用的体现，如2+3=可以画图表示。低年级数形结合思想的渗透符合学生心理发展的特点，为高年级学习较复杂的数学问题提供了有效的解决方法。

2数形结合思想在发展学生空间观念、几何直观中的重要作用

数形结合思想的渗透在发展学生空间观念和几何直观上最为典型。提到空间观念和几何直观，我们就会直接想到形，没有数，形就没有具体的意义，所以数形不分家。在学习面积和体积相关内容时，数形结合思想的渗透与应用尤为重要。《圆柱和圆锥》这一单元的学习中，我充分利用直观形体教具让孩子们在比较中发现，圆柱是由两个底面和一个曲面组成的，圆锥是由一个底面和一个侧面组成的;感受圆柱的高是两个底面之间的距离，有无数条，圆锥的高只有一条，是顶点到地面圆心的距离;在动手操作中，直观认识圆柱的侧面展开图是长方形，圆锥的侧面展开图是扇形;最后在旋转中感受圆柱和圆锥的形成，以长方形的一条边旋转可以得到圆柱，以直角三角形的一条直角边旋转可以得到圆锥，并进一步观察研究各部分的对应关系。并且我让孩子们自己制作圆柱和圆锥，自主探究他们的面积和体积计算公式。发展学生的空间观念和几何直观离不开数形结合思想的应用。

3数形结合思想在发展学生数据分析观念、运用能力、推理能力、应用意识中的重要作用

数学学习的目的是为了解决数学问题，数学问题是否能顺利的解决要看孩子们的数据分析观念、运用能力、推理能力、应用意识，因此，我将这四大核心素养放在一起进行研究讨论。从低年级加减相关的简单数学问题到高年级多步骤的复杂的解决问题，从题意的理解到问题的解决，最好的方法就是运用数形结合思想，将题意通过形来展现，很容易理解，思路也会因为画图过程而清晰呈现。如有关分数的解决问题时，如右图，利用线段图来呈现题意，简单明了。

4数形结合思想在发展学生模型思想、创新意识中的重要作用

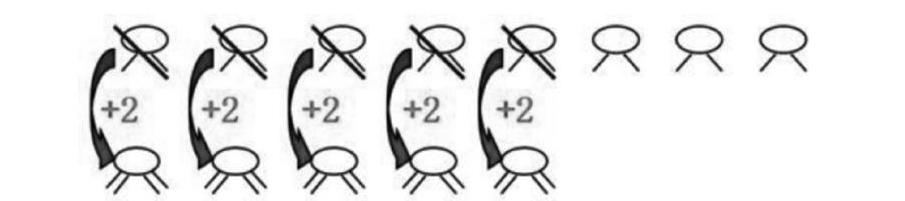
一个模型的建立是为了另一个模型的诞生，那就是创新，所以我将模型思想和创新意识放在一起进行讨论。数形结合思想的应用就是模型思想的建立，建模的过程就是数形结合思想的应用过程，在教授鸡兔同笼模型问题时，我将鸡兔简化为四条腿和两条腿动物，用假设法以图示的形式画出来，如下图，孩子们极易理解。

總之，在小学数学的教育教学中，数形结合思想的渗透与应用是发展学生核心素养的重要举措。数形结合思想的渗透与应用为所要解决的数学问题提供了现实的可能性，简化了学习的过程和步骤，开发了学生的创造性思维，使枯燥的数学变得更加生动、形象、有趣，最终发展孩子们的核心素养。

作者简介：熊安竹，（1983-11）女，汉，山东烟台，研究生，一级教师，小学数学;曹少燕，（1970-11）女，汉，山东烟台，本科，一级教师，小学数学。