巧设问题,打造数学技能教学课堂的美
江古月


【摘要】问题是数学的心脏,一个好的课堂问题的提出,内涵丰富,在问题解决的过程中可以让学生获取知识,提高能力。数学操作技能课的教学往往通过老师讲解,学生模仿和练习,也能把这个技能教给学生,但是从学生实际掌握的效果来看,情况并不十分理想。作为一线教师应该关注儿童,通过问题驱动,设置完整的问题链,来调动学生学的兴趣。
【关键词】问题;技能教学;学习兴趣
“根据方向和距离在平面图上表示物体的位置”是苏教版小学数学六年级下册“确定位置”单元第二课时的内容,在第一课时的教学中,学生已经初步学会了用方向和距离描述物体位置的方法,因此在平面图上表示物体的位置并不会有太大困难,同时这也是一种基本的操作技能。但是作为一节公开课,要求会更高一些。老师们在平时的培训学习中也很少听到这样的技能教学课,因为这样的技能教学容易降低学生的思维水平,孩子们缺少思考与探究,更缺少猜想与创造,所以老师们都不愿意选择这样的课堂进行公开展示。是不是这样的内容就不重要呢?显然不是。如何建构学生的知识体系,培养学生的空间观念,让学生从形式模仿走向真正的意义建构,笔者在教学中进行了初步的实践和思考。
一、生活问题,激活已有知识经验
【片断一】
师:阳春三月,正是我们扬州的旅游旺季,为了便于游客游玩,我们可以绘制一幅扬州景点平面图。
师:文昌阁是扬州的地标建筑,如果以文昌阁作为观测点,最受欢迎的瘦西湖,在地图上的位置谁能来介绍一下?
生:瘦西湖在文昌阁的北偏西30 °方向4千米处。
引导复习一:我们上节课学过的4个方向:北偏东,北偏西,南偏东,南偏西,它们都是以正北和正南为基准来确定方向的。
引导复习二:度数是怎么看出来的?是这条射线与正北方向的夹角。
引导复习三:距离又是如何确定的?关注比例尺和图上的距离。
总结:在平面图上,我们要准确描述物体的位置,需要知道三要素——方位、角度以及應用比例尺计算出的实际距离。这是我们之前学习过的一种从面到线再到点不断精确地确定位置的方法。
反思:当学生面对新的数学问题时,教师能从现实生活中挖掘好的问题“原型”,找到数学知识本身的“影子”,帮助学生回忆与新知学习相关的已有知识经验,再呈现给学生,那么学生的感知肯定会很深刻。上述教学中,笔者没有沿用教材中某海域岛屿图,而是采用了绘制家乡扬州的景点平面图的情境,更贴近学生的生活,激发学生的学习兴趣,激活学生原有的知识经验。教师提出问题:“瘦西湖在地图上的位置谁来介绍一下?”重点复习三个方面:一是大概区域可以用北偏东、北偏西、南偏东、南偏西来表示;二是角度如何确定;三是距离如何确定。“面— 线—点”的深化过程,让学生感受到在平面图上表示物体位置时也是按照这样的思考顺序,这是对旧知的复习,同时也是为新知打下基础。显然,这样的复习是很有必要的,通过问题情境的设置,将数学知识点巧妙应用在生活中,融会贯通。
二、探究问题,提升问题解决能力
【片断二】
师:如果以文昌阁作为观测点,想在这幅图上表示出东关街的位置,你需要知道哪些信息呢?
生:方向、角度、距离。
师:要想准确画出它的位置,我们需要准备哪些工具?有可能会遇到什么问题?和你的同桌商量一下。
生:量角器、直尺。
生1:我觉得在画图前应该要先确定它的大概位置。
生2:画的时候角度不能量错了。
反思:华应龙老师执教过“角的度量”一课,也是一节数学技能教学课,他提出一些思考:为什么教得那么累?传统的技能训练课怎么上?技能训练课的意义在哪里?总的来说还是要让学生了解知识间的联系。本节课上,笔者没有直接告知学生我们怎么去确定物体的位置,而是先让学生通过交流,提出问题:“要想表示东关街的位置,我们需要知道哪些信息?需要准备哪些工具?”这应该是操作技能课所必备的基础。要让学生感知到今天的新知和以前的操作练习有什么不一样的地方,从信息收集到工具准备,这些都应该是我们的关注点,这些都伴随着学生的成长与进步。
三、核心问题,有效突破教学难点
【片断三】
课件出示三幅图。
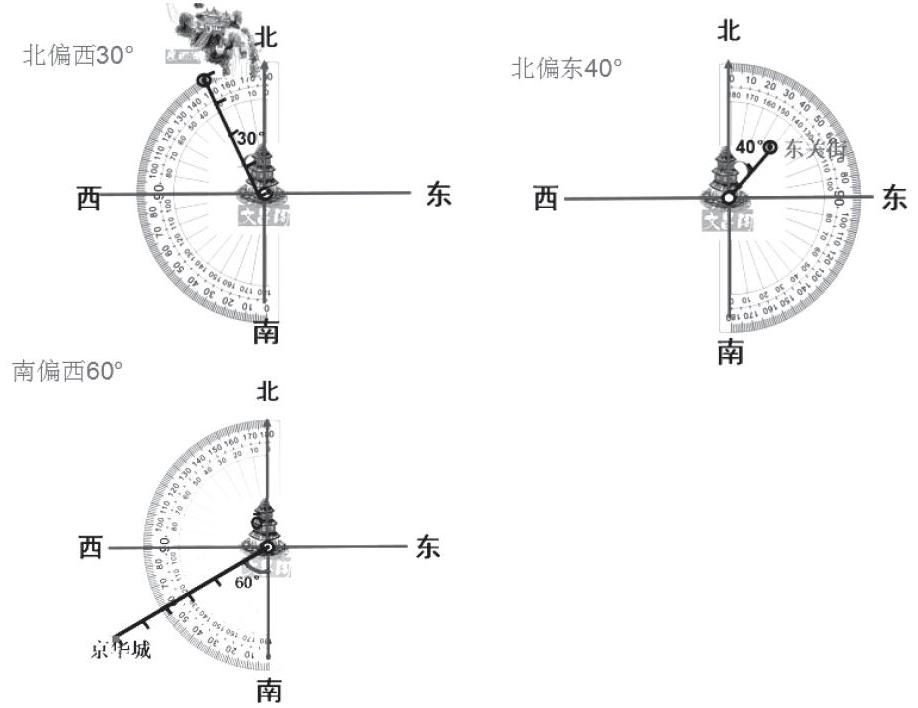
师:仔细观察三幅图上量角器的摆放,你发现了什么?
生:我发现量北偏西、南偏西时,量角器的半圆部分都是放在左边,而量北偏东、南偏东时,量角器的半圆部分都是放在右边。
师:北偏东和南偏东摆放位置是一样的,量角度时也是一样吗?
生:不一样。量北偏东的角度时,看量角器外圈刻度,0刻度线对准正北方向;量南偏东的角度时,看量角器内圈刻度,0刻度线对准正南方向。
师:看来,在确定角度时,量角器的摆放也是很有讲究的。
反思:课堂教学问题的提出首先要立足于知识本质,体现教学内容的重点,能够引导学生去思考,引领学生自主探究,最终能够突破教学的难点。通过几次试教,笔者发现学生的易错点就在画角度环节。如何突破这一难点?“仔细观察三幅图上量角器的摆放,你发现了什么?”通过这一问题的提出,使问题的聚焦点集中在量角器的摆放上,呈现出三个量角器的对比摆放,学生很容易发现其中的异同:北偏西、南偏西量角器摆的位置都是一样的,但是要找到不同的0刻度线,表示北偏东、南偏东也是同样的道理。教师通过对比演示,以及核心问题的提出,将多种表达方式有机整合,巧妙化解教学难点,让学生善于观察,善于发现,思维走向成熟。一个问题的提出要以激发学生解决的需要为突破口,并在兴趣的激励下,通过自主探索去掌握新知识,引领学生深度学习,促进学生数学素养的形成。
四、“诱错”问题,提升学生思维水平
【片断四】
出示扬州景点平面图,引导学生根据提示寻找目标位置。
出示目标1在文昌阁北偏西 60°方向 3千米处。
师:哪一个位置是目标1呢?
生:A那个点。
师:你是怎样想的?
生:目标1在文昌阁的北偏西,因此只有A点和B点,而A点的位置大概就是 60°。
师:你们能验证自己的想法吗?
学生用量角器在作业纸上操作验证。
出示目标 2在北偏东 15°方向2千米处。
师:简单,北偏东15°嘛,肯定是C点。和老师想法一样的举手。
(大部分学生纷纷举手)
师:有没有其他意见?你还有问题需要提出来讨论吗?
生1:老师是不是给咱们设陷阱啊?肯定是C点吗?会不会有其他可能?
生2:目标2是不是在文昌阁的北偏东 15°方向2千米处?
生3:题目上面没有明确说。
生4:老师,我有疑问,请问目标2是在谁的北偏东 15°方向2千米处?
题目重新出示:目标 2在目标1的北偏东 15°方向2千米处。
(生恍然大悟,開始讨论)
生5:我觉得是B点。C点的位置是在文昌阁的北偏东15°方向,而题目中目标 2是在目标 1的北偏东 15°方向,我们观察的点是目标1,而不是文昌阁,所以我觉得是B点。
生6:目标 1是在文昌阁的北偏西 30°,而目标 2的位置在目标 1 的北偏东 15°,二者的观测点不同。
师:看来,确定位置的时候还要注意观测点。这也是一个很重要的信息。
反思:张兴华老师在《儿童学习心理与小学数学教学》一书中指出:“学生思维的开启需要各种刺激和诱因,而各种刺激和诱因中最有价值的莫过于由疑问引起的思维。质疑是思维的导火索,是学习的内驱力,它能使学生的求知欲由潜伏状态转入活跃状态。”由于本节课教学重点是用方向和距离确定物体的位置,学生的关注点很容易就放在方向和角度上,而忽略了观测点这一重要信息。“有没有其他意见?你还有问题需要提出来讨论吗?”让学生学会质疑,学会反思,提高了学生的问题意识。通过让学生寻找目标点,将枯燥的练习变得充满生机活力,“这太简单了,肯定是C点呀”,教师故意诱错,引学生“上当”,风趣幽默的同时更多的是给学生带去思考与质疑。经过孩子们的这番争论,点燃了他们的思维火花,使之产生好奇,再逐步引导孩子们对问题进行分析、解决。整个过程中,生生之间通过交流、质疑,获得了属于自己的成功与满足,令人印象深刻。数学课堂注重学生的思维训练,教师也渴望在课堂上听到不一样的声音,因为这些声音,才是学生真正自主思考的呈现;如果没有这些声音,完全听由老师讲学生听,那样的课堂就犹如一潭死水,没有半点生机。
数学课堂上,无论是老师提的问题,还是学生提的问题,都是鲜活的资源,都要静静思考,师生共同进步,迸发思维的火花。孩子们体验数学、经历数学的学习才是理解性的学习,这样的课堂才是本真的、充满活力的课堂。
【参考文献】
[1]史厚勇.引领思维冲突 完善自我建构[J].中小学教学研究,2014(6).
[2]郜晓定.从粗略到到精确[J].小学数学教育,2017(5).
[3]张兴华.儿童学习心理与小学数学教学[M].江苏教育出版社,2011.

