基于Kummer曲面的RFID标签*

林齐平,张方国

1.兴唐通信科技有限公司,北京100191

2.中山大学数据科学与计算机学院,广州510006

3.广东省信息安全技术重点实验室,广州510006

1 简介

椭圆曲线密码(Elliptic curve cryptography,ECC)是比较有名并用得很多的公钥密码.ECC是由Koblitz[1]和Miller[2]首先独立提出的.对给定的安全水平,椭圆曲线密码系统的密钥长度比其它的公钥密码更短,因此ECC被广泛接受并应用于资源受限的环境中.1989年,Koblitz提出ECC的扩展,即超椭圆曲线密码(HECC)[3],随后跟从HECC的研究人员也有很多.现在HECC的应用也慢慢跟上来了.从安全水平来说,有限域GF(2163)上的ECC和域GF(283)上的HECC被认为安全性等价于1024比特的RSA[4].

(超)椭圆曲线密码的主要运算是标量乘 [k]P,其中 P为椭圆曲线 E上一个点 (或者超椭圆曲线Jacobian的一个除子),k为一个整数.已经有很多方法对(超)椭圆曲线上的标量乘计算进行优化加速了.

自从 Cantor[5]的开创性工作以来,超椭圆曲线的标量乘计算就一直采用 Cantor的算法.在上世纪 90年代,为了更有效地计算,Flynn给出了亏格 2超椭圆曲线的 Jacobian的计算公式[6].十年前,Duquesne继续并推广Flynn的工作,并得到Kummer曲面上的公式.Duquesne的计算公式的效率能与通常的标量乘计算方法相匹敌[7–9].Gaudry等人使用theta函数基于Kummer曲面也提出亏格2曲线的快速标量乘方法[10,11].

在特征为2的有限域上,对应的Kummer曲面的标量乘都有快速计算公式.在相同安全水平下,某些类型的曲线对应的Kummer曲面的标量乘甚至比最好的椭圆曲线标量乘还快.由于标量乘很有效而且只需要很少的寄存器,可以用于低能耗、芯片和计算时间受限的轻量级密码系统,比如RFID标签上.

在 1999年,Smart等人使用亏格 2的 Kummer曲面快速标量乘设计了一个 Diffie-Hellman协议.2017年,Renes等人[12]使用 Kummer曲面快速标量乘提出 qDSA,即商数字签名算法.在 2018年,Costello[13]使用Kummer曲面加速基于超奇异同源的密码计算.但是,在Kummer曲面上构造其它协议或者加密方案特别少.需要通过精巧设计,避免Kummer曲面上的加法计算,才能得到运行在Kummer曲面上的协议.

在本文中,我们把Schnorr的鉴别协议推广到Kummer曲面上并用于构造RFID标签.

RFID(Radio-Frequency Identification)标签是用于鉴别目的的小设备,广泛应用于供应链管理,比如奢侈品的防伪等等.目前用于防伪技术的RFID还处于初级阶段.很多鉴别和隐私保护协议都使用对称密码[14–16].但是,如果在RFID标签中使用对称密码,那么需要在数据库中安全地存储私钥.而且,当读取RFID标签时,为了在数据库中找到正确的密钥需要进行复杂的搜索.这个过程会浪费很多时间,特别是在超大型应用中更是如此.

最近已经有应用于RFID标签的相应的基于公钥的协议.目前基于非对称密码的协议可以分为两类.

(1)一类是使用椭圆曲线方法[17–20].在这类方法中,为了抵抗侧信道攻击,ECC的标量乘通常使用Montgomery阶梯方法.如果鉴别协议不需要y坐标的话,标量乘还可以使用只用x坐标来计算[21].

(2)另一类使用超椭圆曲线.Fan等人[22,23]使用HECC构造了一个RFID标签协议.他们使用的超椭圆曲线的参数为h(x)=x和f(x)=x5+f3x3+x2+f0.

我们在表1中比较了ECC和HECC的计算复杂性,其中I为域的逆运算,M为乘法运算,S为平方运算.

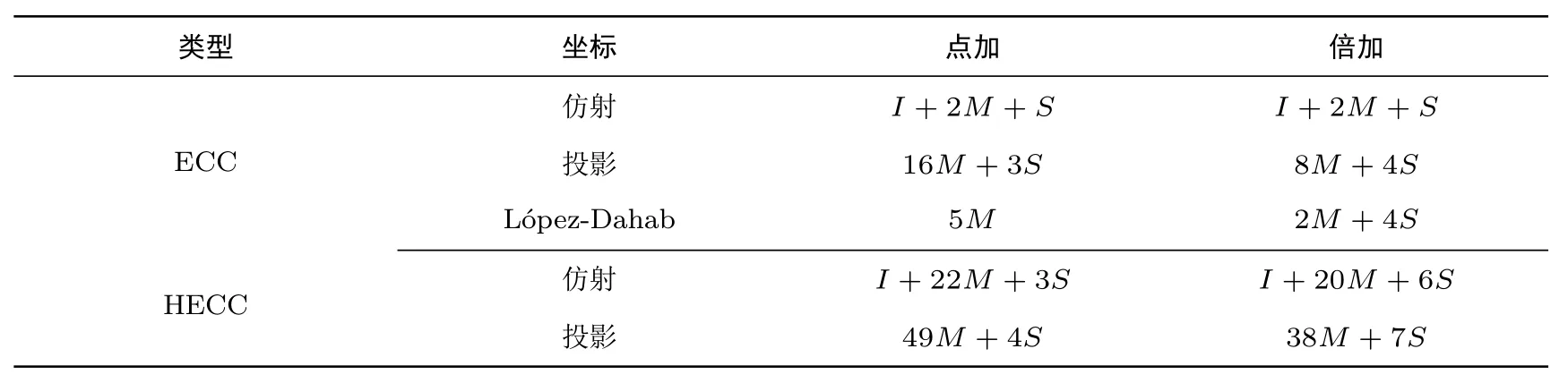
表1 特征2的标量乘比较[4]Table 1 Comparison of scalar multiplication in characteristic 2[4]

本文的组织如下:在第 2节中,我们简单描述Kummer曲面.在第3节中,我们给出了我们的基于Kummer曲面的鉴别协议.在第4节中,我们分析了基于Kummer曲面的RFID标签所需要的资源.第5节是本文的总结.

2 预备知识

在上世纪 90年代初期,Flynn提出了亏格 2曲线的Jacobian公式.Flynn的公式很有效,在1999年,基于Flynn的结果,Smart等人提出了一个快速密钥交换协议.后来,基于Flynn的公式,Duquesne提出Kummer曲面计算标量乘的公式.在本节中,我们描述GF(2n)上的Kummer曲面.

2.1 GF(2n)上亏格 2曲线的分类

定义在特征为2的有限域上的亏格2曲线如下:

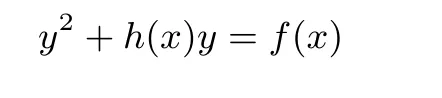
其中

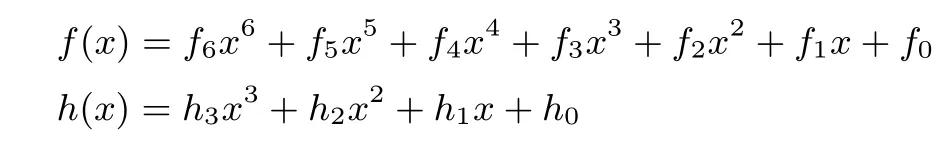
事实上,我们只关心型为

的曲线.亏格2曲线可以分为以下三类[24]:

(1) 类型 I:h20;

(2) 类型 II:h2=0,h10;

(3) 类型 III:h2=h1=0,h00.

在本文中,我们只针对类型为 II的亏格 2曲线.任何类型 II曲线可以定义为型如y2+xy=x5+f3x3+εx2+f0的方程,其中ε∈{0,1}.类型II的同构类大约有2q2.因此很容易能找到符合密码学应用的类型II的曲线.

2.2 Kummer曲面

对每一个特征为2,类型为II的亏格2曲线,存在如下一个P3上对应的Kummer曲面K[8]:

其中

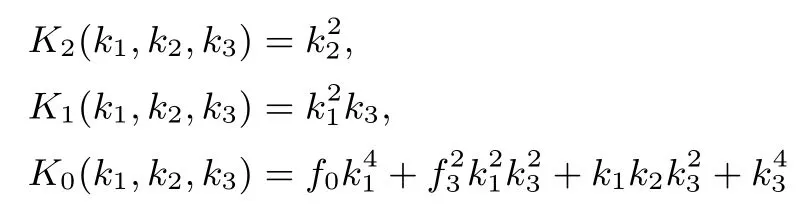
在本文中,我们令 (k1,k2,k3,k4)为 Kummer曲面上一个元素.除了阶为2的点之外,从 Jacobian到P3的映射是2:1的关系.

当Jacobian映射到P3上时,群的运算法则丢失了.Kummer曲面上的加法公式不再保持,因此我们把Kummer曲面上的加法称为伪加法公式.给定Kummer曲面上的两个元素A和B,当且仅当我们先知道A−B的值之后我们才能计算A+B的结果.Montgomery阶梯方法恰好可以用于计算该过程,因为在Montgomery阶梯方法中A−B在每一步中都保持不变.

算法1亏格2曲线的Montgomery阶梯标量乘算法Input:D ∈ J(K)and k=(kn−1,···,k0)2 ∈ N Output:κ(kD),kD 在Kummer曲面上的象1初始化 (A,B)=((0,0,0,1),k(D)),其中(0,0,0,1)为J(C)的单位元在Kummer曲面的象.2for i=n−1 down to 0 do 3 if ki=0 then(A,B)=(2A,A+B);5 end 6 else if ki=1 then 4(A,B)=(A+B,2B);8 end 9end 10返回A 7

在每一步中,Montgomery阶梯方法计算一个加法和一个倍加,这种方法恰好可以抵御侧信道攻击.Duquesne提出的类型II曲线的伪加法和倍加公式如下[9].

命题 1令G是特征为2的有限域,C为定义在G上类型为II亏格2的曲线.κ为从JacobianJ到Kummer曲面的映射.令A,B∈J(C),并且κ(A)=[k1,k2,k3,k4],κ(B)=[l1,l2,l3,l4]分别为它们在Kummer曲面对应的象.假设A−B已知,并且k1(A−B)=1.那么伪加法公式如下:

α=k1l4+k2l3,

β=k4l1+k3l2,

k1(A+B)=(α+β)2,

k2(A+B)=(k1l3+k3l1)2+k1(A+B)k2(A−B),

k3(A+B)=k3l1α+k1l3β+k1(A+B)k3(A−B),

k4(A+B)=αβ+k1(A+B)k4(A−B)

倍加公式如下:

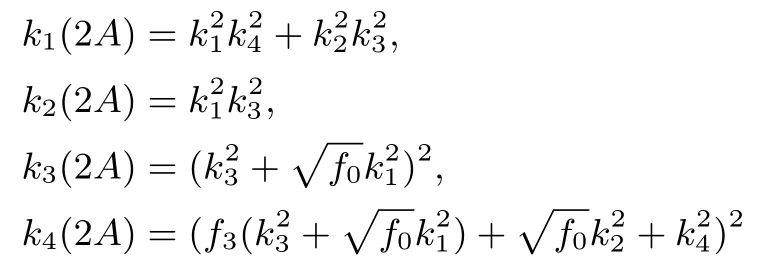
3 Kummer曲面上的鉴别协议

Schnorr的鉴别协议[25,26]是基于群F∗q或者有限域上的椭圆曲线或者有限域上亏格g的曲线的Jacobian上的离散对数问题的.在本节中,我们把Schnorr的鉴别协议推广到Kummer曲面上.

3.1 鉴别协议

• 输入:系统参数集合(q,f3,ε,f0,P,n).其中q指定有限域,f3,ε,f0定义一个与亏格2类型II曲线相对应的Kummer曲面,P为阶为n的Kummer曲面上一个元素.

• 证明者(标签):证明者的私钥为a,且有Z=−aP.

• 协议的过程:协议包括以下交互信息:

(1)证明者→验证者:{X}.证明者选取r∈RZn,并计算X=rP.然后发送X给验证者.

(2)验证者→证明者:{e}.验证者选取e∈RZn并把它发送给证明者.

(3)证明者→验证者:{y,R}.证明者计算y=ae+rmodn和R=(2ae+rmodn)P,然后把它们发送给验证者.

(4)验证者.验证者接收到{y,R}之后,他开始计算yP,eZ并验证pseudo-add(yP,eZ,R)是否等于X,如果验证通过则接受,否则拒绝.

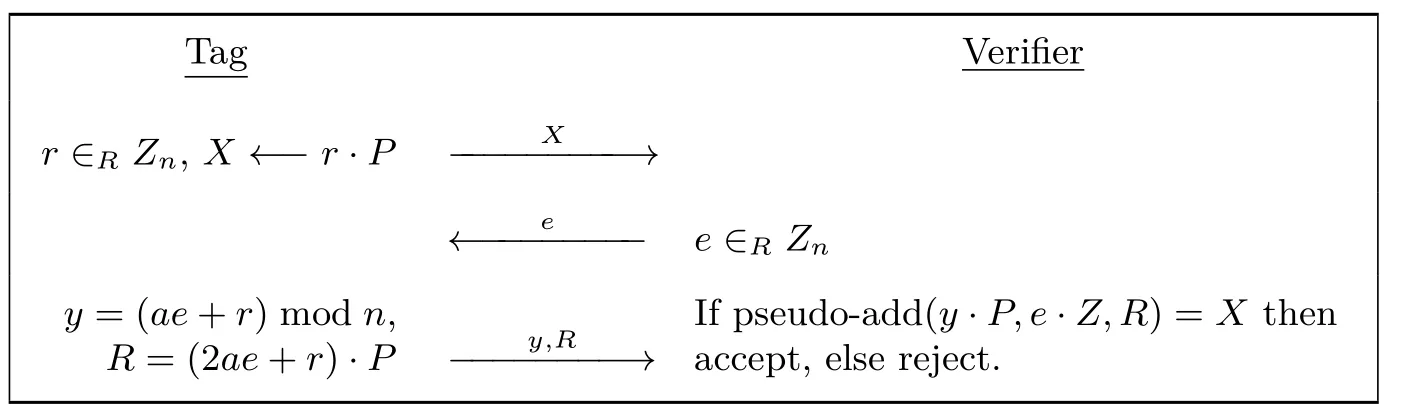
图1 Kummer曲面上的Schnorr协议Figure 1 Schnorr’s protocol on Kummer surface

3.2 协议的分析

我们的鉴别协议可以完全运行于 Kummer曲面上.协议的正确性可以验证如下.当验证者接收到{y,R}后,他计算Kummer曲面上的标量乘yP和eZ.然后他有四个点yP,eZ,R和X,因此他可以使用Kummer曲面上的伪加法公式验证yP+eZ是否与X相等.伪加法公式能成功运行是因为验证者知道R=yP−eZ的值.

从图1可以看到,证明者需要计算两个标量乘和一个模乘,验证者需要两个标量乘和一个伪加法计算.与原来的协议相比,为了能在Kummer曲面上执行Schnorr鉴别协议,我们需要额外多计算一次标量乘.但是,因为计算的有效性能抵消掉额外的一次标量乘计算,因此这是可以接受的.

我们的协议的安全性是基于 Kummer曲面上求解离散对数困难问题的.而Kummer曲面离散对数问题的困难性并不低于亏格2曲线的Jacobian的离散对数问题[27].

3.3 基于Kummer曲面的RFID标签

我们可以利用 Kummer曲面的鉴别协议来设计 RFID标签.协议的主要操作是标量乘.设计基于Kummer曲面的鉴别协议主要是硬件中的有限域的有效操作.下一节中我们分析基于 Kummer曲面的RFID标签的资源情况.

4 Kummer曲面上的操作

在本节中,我们将分析Kummer曲面上的标量乘所需要的寄存器、点压缩和解压缩过程.

4.1 标量乘所需要的寄存器

表2,3是运行在Kummer 曲面上的伪加法公式和倍加公式的寄存器情况,其中前 5个寄存器是参数和点κ(A−B),分别是R1=,R2=f3,R3=k2(A−B),R4=k3(A−B),R5=k4(A−B).不失一般性,我们假设k1(A−B)=1.从表2和表3可以看到,运行Kummer曲面上的伪加法和倍加总共需要13个寄存器.

表2 特征2的伪加法公式Table 2 Points pseudo-addition in characteristic 2

表3 特征2的倍加公式Table 3 Points doubling in characteristic 2

为了能抗侧信道攻击,非对称密码在计算标量乘的时候需要使用 Montgomery阶梯方法.Montgomery阶梯方法计算结构稳定,因此天然能抗简单的能量攻击和时间攻击.同时 Montgomery阶梯方法还很适合于硬件实现.

4.2 点压缩与解压缩

命题 2Kummer曲面上的点(k1,k2,k3,k4)可以使用最多两个有限域元素加上1比特来表示.

证明:Kummer曲面是属于空间P3上的,因此一个点可以用3个有限域元素来表示.Kummer曲面上的单位元为(0,0,0,1).因此,Kummer曲面上除了单位元以外,一个点(k1,k2,k3,k4)中的k1,k2,k3最少有一个非0.不失一般性,假设k1̸=0,那么令k1=1.现在点(k1,k2,k3,k4)可以由(k2,k3,b)来表示了,其中b∈{0,1}为k4的最低比特数.给定k2,k3,我们有以下方程成立:

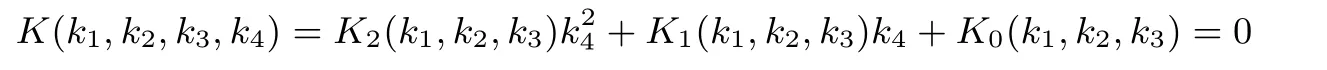
其中K2(k1,k2,k3),K1(k1,k2,k3),且K0(k1,k2,k3)已知.该二次方程有两个根,最后我们可以使用b来确定正确的k4的值.

4.3 性能分析

在文献[22,23]中,Fan等人的实验结果表明HECC也可以用于RFID标签设计上.他们用于构造RFID标签而选取的曲线同样也是亏格2中类型II的曲线.但是HECC的缺点是标量乘的计算太复杂.经过近年来的发展,在新的坐标公式和技术下,HECC的实现性能已经和ECC相当了.

我们的基于Kummer曲面的RFID标签方案比其它亏格2的方案更优.而且,我们方案的性能还与某些ECC方案的实现性能不相上下.

记M为有限域F2m的乘法,S为F2m上的平方运算.有限域F2m的二次扩域为F22m.在二次扩域F22m中,两个元素相乘

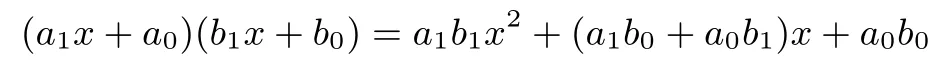
为经典的计算,需要4M和1个加法.使用Karatsuba算法[28]后,两个扩域元素相乘为

(a1x+a0)(b1x+b0)=a1b1x2+((a1+a0)(b1+b0)−a1b1−a0b0)x+a0b0

只需要3M和4个加法计算.而二次扩域上的平方计算量通常都比两个基域的平方计算量要多.

不管是使用经典的还是 Karatsuba算法,二次扩域中的一个模乘计算量要比3个基域的模乘计算量多.我们忽略加法计算量,并假设基域的模乘与二次扩域的模乘的计算量比率为1:3,平方的计算量的比率为1:2.那么表4表示在相同安全水平下的标量乘比较 (假设ECC使用有限域F22m而 Kummer曲面使用有限域F2m).其中在特征为2的有限域中,在多项式基中通常S=0.3M,而在规范基中平方运算就是移位运算,因此S=0.

表4 同等安全水平下ECC和Kummer曲面计算量比较Table 4 Computation of ECC and Kummer surface over same security level

可能基于Kummer曲面上的RFID标签的计算时间在RFID标签一侧比ECC的慢,但是在验证者一侧,基于Kummer曲面上的RFID标签的计算速度确实比较快.

5 总结

在本文中,我们扩展了Schnorr的鉴别协议到Kummer曲面上,并用它来构造一个巧妙的RFID标签.我们的结果表明基于 Kummer曲面的 RFID标签方案比其它亏格为 2的方案更好.而且,与基于ECC的RFID标签相比,我们的方案在验证的时候能节省百分之13到15的计算量.在应用方面,RFID与区块链可以结合起来组成一个闭合的信任链,从生产到消费全生命周期可以实现可追溯、去信任等,这在将来将会有很多这方面的应用.