基于SA+BP混合算法的动力电池放电峰值功率估算

朱 浩, 张文博, 邓元望, 李 梦, 吉 祥

(湖南大学 机械与运载工程学院, 湖南 长沙 410082)

动力锂电池的短时峰值功率能为电动汽车整车系统的功率分配作参考,能够衡量车辆的爬坡性能和刹车时制动能量回收功能[1-3],以及有效防止电池包过充、过放现象的发生.目前对于动力锂电池峰值功率的研究大多集中于某单一因素对电池峰值功率的影响,以及改进研究中所使用的电池模型.文献[4]通过试验分析电池的荷电状态(state of charge,SOC)、温度和端电压对于电池峰值功率的影响,结果表明温度对于电池峰值功率的影响最大.文献[5]认为SOC、电池老化等估算值不能作为功率状态估算的影响因素,而应直接使用电池物理模型中的参数来估算电池的在线峰值功率.文献[6]在RC电池模型中加入平行移动的噪声,使用递归扩展最小二乘法来估算电池在不同时长的电池峰值功率.文献[7]为了提高长期的功率预测精度,考虑了扩散电阻对电池模型的影响.

若使用端电压作为峰值功率估算条件,可能会导致估算误差较大,因为端电压在车辆加速时骤降,减速时骤升,跳动过于剧烈.此外,大部分有关电池功率状态的研究中,使用的电池模型为基于物理现象的数学模型,如Thevenin模型、Rint模型等,而电池的充放电是一种复杂的电化学反应.若采用基于数据统计和机器学习算法的神经网络建立电池模型,则可以更加准确地模拟电池的特性.文献[8]运用小波神经网络来模拟电池的动力特性,使得电池的能量状态(state of energy,SOE)估算误差小于4%.文献[9]提出了一种基于人工神经网络的电池模型,使得SOC估算的均方根误差小于2.5%,最大误差小于3.5%.文献[10]建立了BP神经网络电池模型,进行了静态和动态电流脉冲试验,试验结果表明该模型健康状态(state of health,SOH)的估算误差小于8%.

笔者采用前馈神经网络建立电池峰值功率模型,运用SA+BP混合算法作为模型的训练方法,以克服BP算法局部收敛的缺点,通过仿真结果的拟合程度和误差分析,证明该模型能够精确地模拟电池的功率特性.

1 电池峰值功率估算模型

1.1 模型参数

在实际应用中,电池本身是一个复杂的非线性系统,其放电峰值功率受温度、SOC、欧姆内阻、端电压及电池的老化程度等多个因素影响.若把所有的影响因素都作为模型的输入变量,将会使模型的复杂程度提高,计算量变大,训练时间变长,输入变量之间可能存在的共线性导致模型的估算失真等.因此,在保证模型估算精度和训练效率的情况下,应该考虑能准确反映电池峰值功率特性的变量作为输入参数,同时也需要考虑模型的输入变量可在线获得,以保证模型的实际可行性.

输入参数的选择中,由于端电压在车辆运行过程中跳动过于剧烈,不适合作为模型的输入参数.温度、SOC及欧姆内阻可以考虑作为模型的输入参数,通过文献[11]对电池的SOC、温度和欧姆内阻的共线性分析可知,欧姆内阻与SOC、温度之间存在严重的共线性,若同时作为模型的输入变量会导致估算精度降低,而SOC和温度是由试验设定的,不存在共线性关系,故选取SOC和温度作为输入变量.

输出参数的选择中,若使用电池峰值功率作为输出值,由于电池的个性差异导致各个电池欧姆内阻不同,而电池的峰值功率包含欧姆内阻的发热功率,故欧姆内阻的差异性会降低电池峰值功率估算的精度,故决定使用电池的峰值电流IE作为模型的输出值,代入公式(2)计算电池的峰值功率.

考虑到动力传输过程中的能量损耗和采集误差,选取放电截止电压作为功率计算的电压值,根据欧姆定律计算电池的欧姆内阻.通过电池管理系统(battery management system, BMS)对电池的温度、SOC和欧姆内阻每0.1 s更新一次,代入公式(1)和(2)计算电池的峰值功率:

IE=f(SOC,θ),

(1)

(2)

式中:θ指电池的温度;f指神经网络模型;IE指估算的峰值电流;R1指电池的欧姆内阻;Umin指放电截止电压;P指电池的峰值功率.

1.2 电池模型

神经网络电池模型由输入层、隐藏层和输出层组成.确定了模型的输入和输出参数后,需要进一步确定隐藏层的数量,若使用单隐藏层,模型相对简单,会降低模型估算精度;若使用隐藏层数目太多,会使模型的训练时间变长,计算量变大,收敛速度变慢,且误差不一定最小,甚至会降低其泛化能力等.综合考虑模型的复杂程度及估算精度,笔者决定采用双隐藏层神经网络.隐藏层神经元的数量由经验公式(3)选取:

(3)

式中:a指输入层变量的个数,个;b指输出层的变量个数,个;常数p=1，2，…，10[12];l指神经元的个数,个.

最终通过对模型的训练来确定隐藏层神经元的个数.建立的神经网络电池模型如图1所示，其中E，w和b分别为误差、权值和阈值.

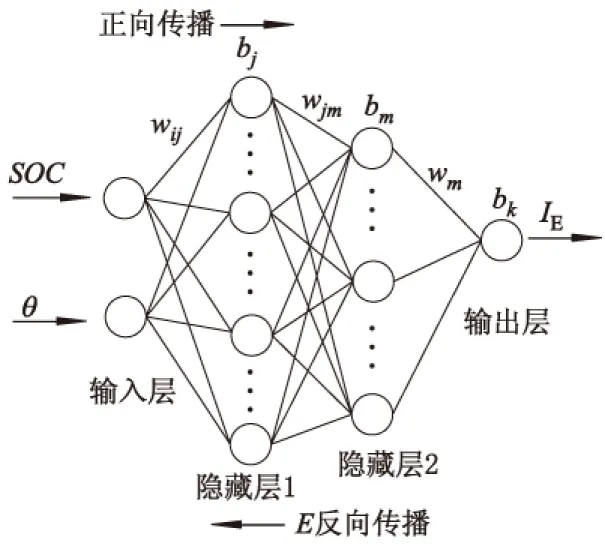
图1 神经网络电池模型

1.3 电池峰值功率估算

1.3.1BP算法

BP神经网络因具有很强的自学能力、泛化能力及非线性函数逼近能力,使其应用广泛.BP网络的学习过程有信号的正向传播和误差的反向传播两部分组成[13].针对笔者建立的神经网络电池模型,在其正向传播过程中,把电池的SOC和温度输入网络中,经过隐藏层和输出层后,得到峰值电流IE.信号正向传播的过程如公式(4)-(6)所示:

(4)

(5)

(6)

在误差的反向传播过程中,计算神经网络估算峰值电流与实际峰值电流的误差,将其由输出端反向传播至输入端,用梯度下降法更新网络的权值和阈值.网络的训练过程持续不断地进行,直到输出误差降低到可接受的程度,或满足其他终止条件才停止训练.输出层神经元的连接权值和阈值的更新过程如公式(7)-(11)所示,其他层参数的更新过程与其类似，即

(7)

(8)

(9)

wm=wm+Δwm,

(10)

bk=bk+Δbk,

(11)

式中:y为实际的峰值电流;α为学习率,可以采用自适应的学习率,在接近极值点时,使用较小的学习率,反之则使用较大的学习率.

1.3.2SA+BP混合算法

为提高模型的估算精度和解决BP算法的局部最优问题,采用SA+BP的混合算法作为模型的训练方法.SA算法的关键参数包括Markov链长度Lx、截止温度θf和温度变化率β等.其中Markov链长度由经验公式(12)确定:

Lx=100N,

(12)

式中:N指样本总数,个.

利用Matlab神经网络工具箱与Matlab编程语言相结合,编写SA+BP混合算法,该算法对模型的训练过程如图2所示,其中xc,xL和xB指神经元的连接权值和阈值,xc指当前值,xL指上次值,xB指目前最优值;Et指目标误差,Ec指当前误差,EL指上次误差,EB指目前训练最小误差;P指降温的概率.

图2 SA+BP混合算法训练流程图

训练过程中,当xc收敛到一个极值点时,比较上次误差EL与目前的最小误差EB,若EL小于EB,则更新EB和xB,而后对xc进行随机扰动,使其偏离目前的极值点,若满足降温概率,则对温度t进行更新,否则直接进入下次训练中.只有当温度降到θf或满足网络设置的目标误差Et时,则停止训练,输出训练网络所需的参数xB.

2 仿真及结果分析

2.1 峰值功率试验

目前,动力锂离子电池峰值功率试验方法主要包括美国Freedom CAR项目提出的混合脉冲功率特性(HPPC)测试法和恒功率测试法[11],本研究中采用HPPC测试法.试验中,当电池在恒定电流下持续放电t秒后,端电压降至放电截止电压Umin时,此恒定电流即为电池在该状态下的峰值电流.根据GB/T 31485—2015《电动汽车用动力蓄电池安全要求及试验方法》中功率试验方法规定的纯电动汽车峰值功率持续时间为30 s[14],故取t=30 s作为峰值电流的持续时长.试验以5节ICR18650/26V1型号的三元锂电池作为研究对象,试验平台由上位机、BTS20充放电机和恒温恒湿箱组成,其连接如图3所示.

对于试验测试点数的选取,综合考虑了试验时长、材料花费和模型训练时间等因素,温度为5～45 ℃,每隔20 ℃设置一个温度点;SOC设置为0.20～1.00,每隔0.05设置一个SOC点.在峰值电流试验中,当电池放电至测试点时,将其放置到恒温恒湿箱内静置2 h,之后以I1对电池进行放电,当电池端电压下降至放电截止电压Umin时,记录试验时间t1.HPPC脉冲放电曲线如图4所示.

再次调整动力锂离子电池至放电前的状态,经过2 h静置后,继续以I2对电池进行放电,记录放电时间t2.经过多次循环测试后,得到动力锂离子电池在该状态下的放电峰值电流I与时间t的关系曲线,如图5所示.通过查询法,从拟合曲线中得到电池峰值电流持续时间30 s的峰值电流Imax.共获得245组有效的试验数据.表1为电池峰值电流试验部分结果.

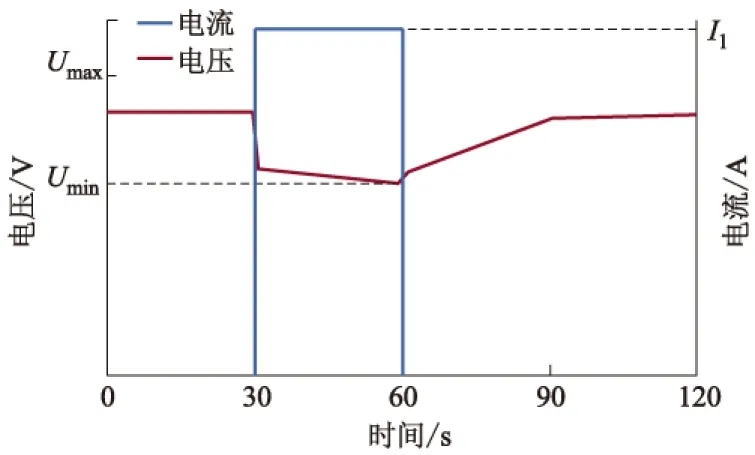
图4 HPPC脉冲放电曲线

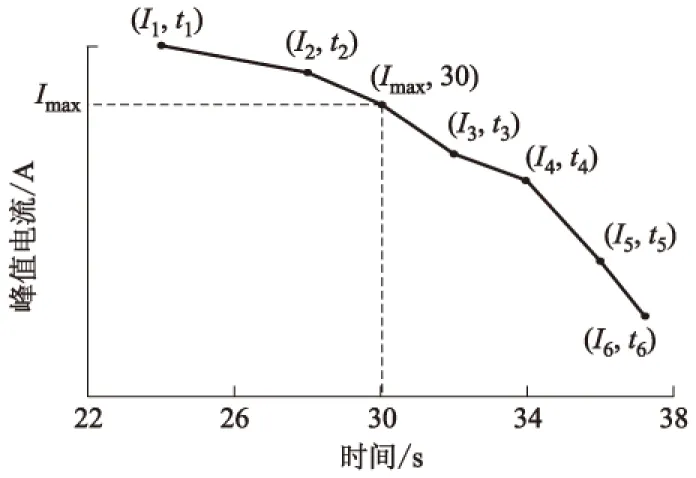
图5 恒定电流放电测试拟合曲线

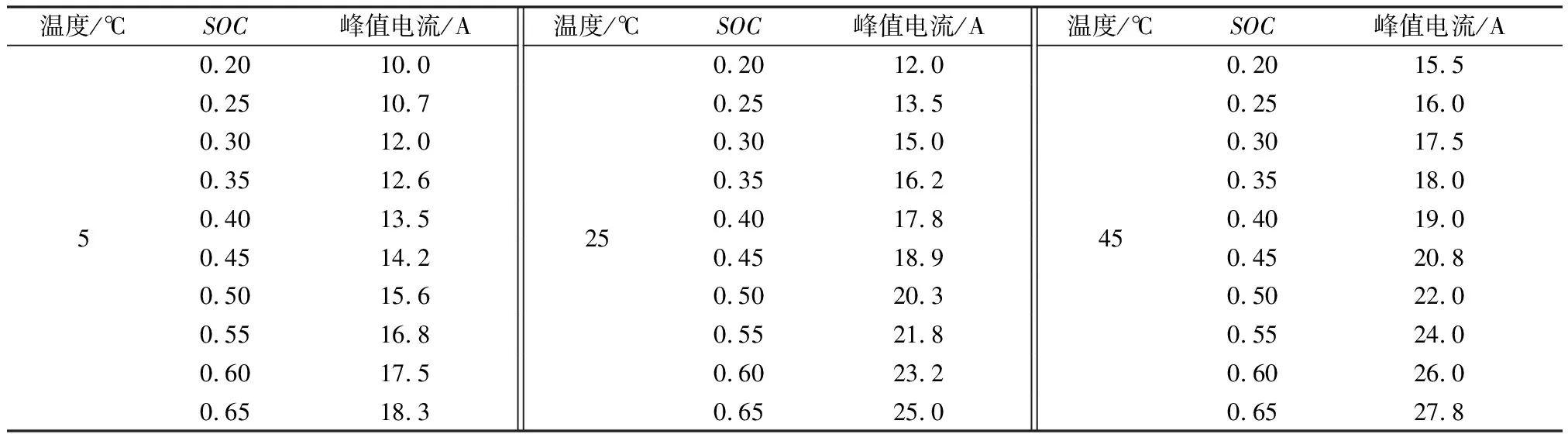
表1 电池峰值电流试验部分结果

2.2 模型的训练

首先选取适合的样本作为训练数据.训练样本量一般约为80%,试验共获得245组数据,故选取200组数据为训练样本;考虑到样本的遍历性,分别选取单个电池在5,25和45 ℃的12,14和14组数据,由于5 ℃下SOC最大约为90%,故选取样本略少于其他温度;为了降低单个电池的个性化差异,提高模型的泛化能力,因此选取 5个电池同等条件下的样本数据.其次,为了提高模型的训练效率和模型精度,需要对样本数据作量纲一化处理,量纲一化处理方法如公式(13)所示,其中yi指相同性质的变量.

(13)

然后把处理后的数据输入网络中,开始进行训练.分别使用BP算法、SA+BP混合算法作为模型的训练方法,通过不断调整激活函数、学习率和隐藏层神经元的数量等,使模型估算值与期望值之间的误差不断减小,直到满足设置的误差范围.最终通过在训练中不断调整神经网络的参数,确定第1,2隐藏层神经元个数分别为8,6个,2个隐藏层和输入层的激活函数为tansing.将估算和实际得到的电流值分别代入公式(2)后,得到估算与实际得到的峰值功率拟合曲线,如图6所示.由图6可知:基于两种算法的估算值与实际值拟合曲线的变化趋势保持一致,基于SA+BP混合算法的估算值与实际值拟合曲线的吻合程度更高.

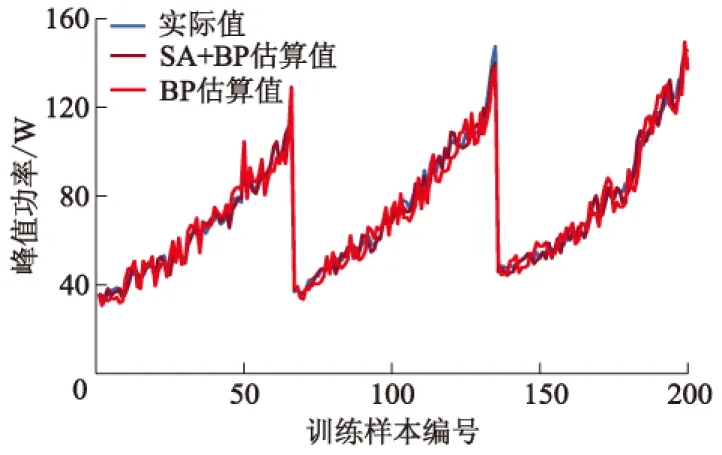
图6 训练样本峰值功率的估算值与实际值对比

图7为训练样本的峰值功率相对误差.表2为基于BP算法和SA+BP算法的训练结果对比.由图7和表2可知:基于SA+BP混合算法估算值的精度明显高于基于BP算法估算值;峰值功率的最大相对误差为7.45%,平均相对误差为3.12%;基于BP算法估算值的最大相对误差为11.91%,平均相对误差为4.67%.由图6,7可知:在峰值功率较小时,基于两种算法的估算值相对误差都较大,究其原因是在功率较小时,即便绝对误差很小,也会使相对误差较大.综上,基于SA+BP混合算法训练的电池模型估算精度更高.

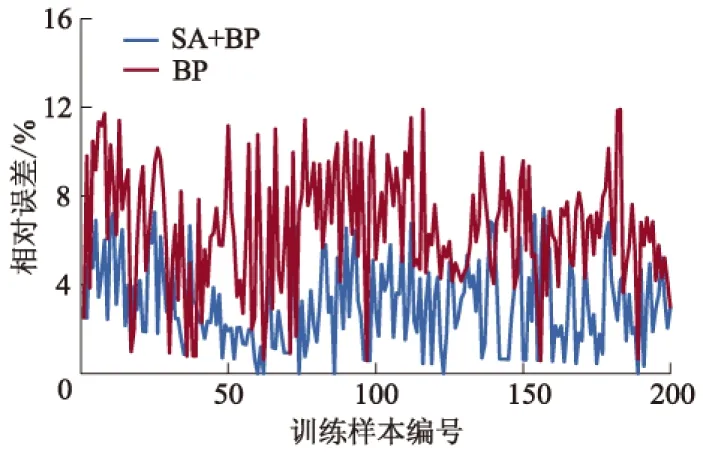
图7 训练样本的峰值功率相对误差对比

表2 基于BP和SA+BP算法的训练结果%

2.3 模型的验证及结果分析

试验共获得245组数据,以其中45组数据作为测试样本,分别对基于BP算法和SA+BP算法训练的模型进行验证,得到峰值功率估算值与实际值的对比散点图,如图8所示.由图8可知,基于SA+BP混合算法的估算值与实际值拟合程度更高,基于BP算法的估算值与实际值的拟合程度相对较低.

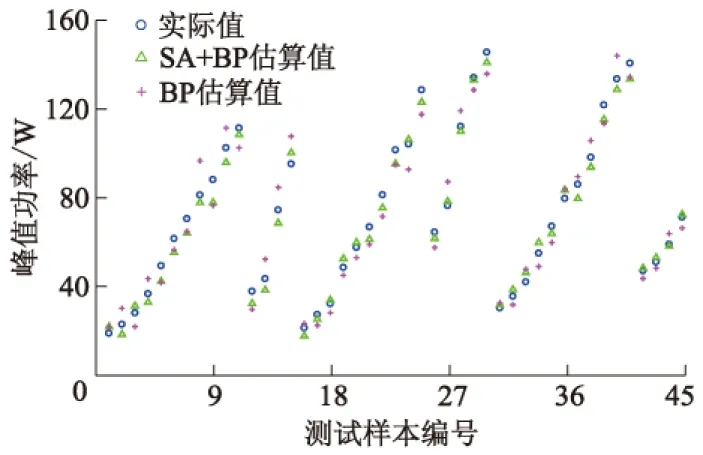
图8 测试样本峰值功率估算值与实际值对比散点图

图9为测试样本峰值功率的相对误差.表3为基于BP算法和SA+BP算法的峰值功率测试结果对比.由图9可知,基于SA+BP混合算法估算值的相对误差不超过10%,而基于BP算法的测试样本中,有接近一半估算值相对误差在8%以上.由表3可知:基于SA+BP混合算法的估算值最大相对误差为9.84%,平均相对误差为4.73%;基于BP算法的估算值最大相对误差是15.94%,平均相对误差是7.71%.由此可知,相比BP算法训练模型的估算精度,基于SA+BP混合算法的峰值功率估算的最大相对误差降低了38.27%,平均相对误差降低38.65%.

图9 测试样本峰值功率的相对误差对比

表3 基于BP和SA+BP算法的峰值功率测试结果%

综上,基于SA+BP混合算法训练的神经网络电池模型,可以提高峰值功率的估算精度,能更加准确地描述电池的功率特性.此模型更适用于高峰值功率估算的场合,而对较低峰值功率的估算精度还有待提高,可通过增加训练样本数量或交叉验证的方式来提高模型的估算精度.

3 结 论

1) 基于数据统计和机器学习神经网络电池模型的建立,使得从研究电池内部复杂的化学反应转移到分析电池的数据特性上,降低了研究的难度.

2) 通过估算电池的峰值电流,并将其代入相应的公式中,以计算电池的峰值功率,而非直接估算电池的峰值功率,可以避免欧姆内阻的差异性导致估算误差增大.

3) 仿真结果表明:相比于BP算法模型的估算精度,本研究中采用基于SA+BP混合算法的估算值最大相对误差降低了38.27%,平均相对误差降低了38.65%,证明该算法训练的电池模型能更加准确地模拟电池的功率特性.

4) 本研究中采用基于SA+BP混合算法训练的电池模型估算值相对误差不超过10%,具有较高的准确性,对于电池峰值功率的研究有重要的理论意义和实用价值.