基于V2V的高速换道轨迹多目标规划

张新锋, 夏八科, 张甫城

(1. 长安大学 汽车运输安全保障技术交通行业重点实验室, 陕西 西安 710064; 2. 长安大学 汽车学院, 陕西 西安 710064)

车辆在高速公路上行驶时,换道作为一项重要驾驶行为,驾驶员需要根据周围车辆的运行状态、间距及道路使用情况,交通管理一系列的交通环境做出合理的分析和判断.一旦驾驶员对换道做出错误的判断,极易导致交通事故的发生.根据统计,在高速公路和快速车道上,约有60%以上的交通事故与换道过程有关.因此,如何提高车辆在高速公路上换道的安全性是一项重要研究内容[1-2].随着智能网联汽车的发展,应用自动驾驶技术可以全面提升汽车驾驶的安全性、舒适性,避免由人为误操作引发的交通事故.而5G通讯技术的发展,极大地提高了车辆与交通环境之间的通讯能力,智能网联汽车得到了快速发展.通过环境感知和通信技术实时获取周围交通状态信息,为车辆规划一条安全高效的换道轨迹,解决由于行驶环境的随机性和复杂性导致换道轨迹规划的难题.

目前,国内外对于车辆换道的研究集中于对车载传感器式智能车辆的研究,而对于网联式智能车辆的换道轨迹规划研究较少.杨志刚等[3]对自由换道场景下不同的换道模型进行了对比分析,并提出等速偏移与正弦函数叠加的换道模型,并从理论上验证了模型的可行性,但并未考虑实际交通状态对轨迹规划的影响.WANG C.等[4]对客车的换道安全进行了研究,提出一种新的安全换道识别模型,与ISO 17387—2008《智能运输系统路线改变决定辅助系统(LCDAS) 性能要求和试验程序》标准相比,该换道安全识别准确率有了显著提高,为车辆的安全换道分析提供了理论依据.H. TEHRANI等[5]以多项式分别拟合车辆换道时的纵、横向运动,并以换道轨迹曲线的平滑度来对其进行评价,对比记录的高速公路车辆换道实际运动信息,多项式拟合的换道轨迹能够提升换道时的舒适性,由于未考虑车辆动力学参数,实用较为困难.LUO Y. G.等[6]将车辆换道轨迹规划转化为以换道时间和换道距离为变量的优化求解问题,使之能够适应动态的交通场景,但未给出目标函数权系数的取值方法.

为了发挥自动驾驶技术在减少交通事故、提升换道效率和道路利用率的巨大优势，笔者以智能网联车辆高速公路自动换道为研究背景,为车辆规划最优的换道轨迹.为了保证换道过程不与其他车辆发生碰撞,建立车辆的换道安全距离模型,通过V2V(vehicles to vehicles)共享交通资源信息,可以有效缩短需求的换道安全距离.车辆换道前对周围行车环境的判断,决定着后续车辆运动轨迹的规划,规划出来的轨迹能够与当前环境相适配.根据车辆换道前后的边界条件,选取多项式函数对换道轨迹进行描述,并建立综合考虑舒适性和换道效率的多目标规划函数,从而对换道时间进行优化选取,最终得到车辆在该行车环境下的最优换道轨迹,与非V2V模型相比得到有效的改进.在CarSim中建立车辆换道交通环境,对V2V换道模型进行验证.

1 换道安全距离模型

车辆准备换道时,安全性作为首要考虑条件,所规划的换道轨迹必须保障换道过程无碰撞、车辆操稳性得到满足.所以在轨迹规划之前,为了保障车辆换道过程不与其他车辆发生碰撞,应该与其他相关车辆间保持一个最小的纵向距离,当满足该最小的安全距离时,能够保证车辆安全地完成换道而不与其他车辆发生碰撞.

本研究采用H. JULA等[7]提出的车辆换道安全距离模型,如图1所示,在车辆M进行换道时,考虑了当前车道前、后车辆Lo和Fo及目标车道的前、后车辆Ld和Fd.但是考虑到实际换道过程中当前车道的后车Fo属于跟车行为,所以不考虑Fo与换道车辆M之间的距离对M换道的影响.

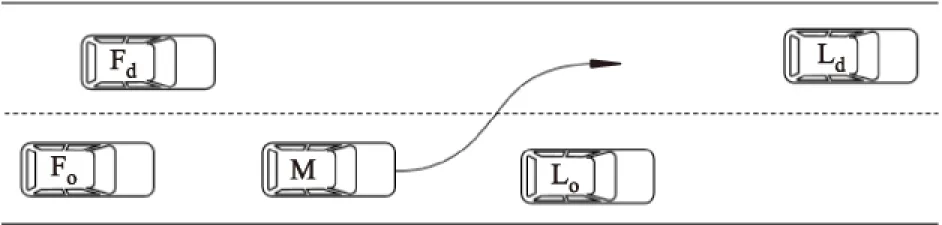
图1 车辆换道示意图

车辆换道涉及到的交通情况比较复杂,通过对模型的简化处理,对换道过程做如下假设: ① 车辆高速换道过程中的纵向夹角较小,在考虑换道安全距离时近似认为车辆以平行移动的方式运动到目标车道; ② 所有车辆都为智能网联汽车,具备V2V功能,且不考虑通信延迟对换道规划的影响; ③ 忽略车辆外形尺寸对换道过程的影响,即认为换道车辆与周围交通车辆外形尺寸上长、宽、高相同; ④ 在规划车辆的换道轨迹时,将车辆的纵、横向解耦,认为车辆的纵向运动和横向运动相互独立.

为了便于后续的处理,将其安全距离模型计算的参考点统一设定为车辆质心,车辆的长度设为L,则换道车辆M与Lo,Ld,Fd换道初始时刻应该保持的最小纵向距离sMLo(t0),sMLd(t0),sMFd(t0)的计算公式为

(1)

式中:aM,aLo,aLd,aFd为各车的加速度;vM,vLo,vLd,vFd为各车的速度;tp为车辆间发生碰撞的临界时间;tf为车辆完成换道时间;t0为起始时间,t0=0.

2 基于V2V的换道安全距离判断

车辆在高速公路上进行换道前,需要根据周围车辆的运行状态,确定安全换道距离是否能够得到满足,如果可以则进行换道,否则只能放弃换道,继续跟车或者制动,对周围车辆进行监测的同时，寻找下一个换道时机.

由换道安全距离模型可知,车辆在做出换道判断时必须能够实时获取周围车辆的运行状态信息,但是就目前基于传感器的自主式智能车远不能满足要求,尤其是相邻车道的交通车运行状态判断.使用V2V通信技术获得周围车辆状态信息(位置、速度、加速度等),对车辆行驶进行提前规划决策,从而减少交通事故、提高交通效率[8].

在车辆M产生了换道动机后,向周围车辆发送换道需求,本车道后车Fo自动进入跟车模式,而本车道的前车Lo和目标车道的前车Ld与后车Fd自动将自己的位置、速度、加速度等行车信息发送给换道车辆M,该换道车车通信如图2所示.

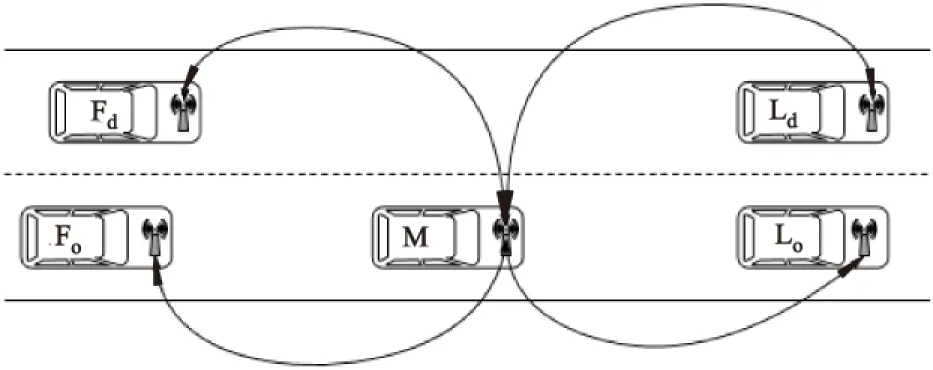
图2 车车通信示意图

以换道车辆质心为坐标原点,前进方向为x正半轴,侧向运动方向为y正半轴.这样车辆M在准备换道时发送换道需求,可以获取到周围车辆Lo,Ld,Fd的运行状态信息(xLoyLovLoaLo),(xLdyLdvLdaLd),(xFdyFdvFdaFd),车辆M根据获取的周围车辆位置坐标和自身的位置坐标,可以判断出其他车辆的相对位置,进一步得到准备换道时刻与各车的纵向距离:

(2)

式中:sMLo,sMLd,sMFd为换道车辆与其他车辆的纵向距离;xM,xLo,xLd,xFd为对应各车位置的横坐标;yLo,yLd,yFd为对应各车位置的纵坐标.

根据得到的周围车辆速度、加速度信息,计算车辆在换道前应该保持的最小安全距离为sMLo(t0),sMLd(t0),sMFd(t0),可以得到该V2V换道距离模型如图3所示.

图3 车辆换道距离模型

控制系统根据位置信息得到的纵向距离sMLo,sMLd,sMFd和计算的换道前应该保持的最小纵向安全距离sMLo(t0),sMLd(t0),sMFd(t0)进行对比: 若sMLo>sMLo(t0),sMLd>sMLd(t0),sMFd>sMFd(t0)同时满足,则能保证车辆M在换道过程不与其他车辆发生碰撞,可以进行换道;否则只能等待下一个满足换道距离要求的时刻进行换道.

3 基于多项式的换道轨迹规划

在车辆进行换道安全距离判断后,当满足换道要求时,需对车辆的换道轨迹进行规划.规划的轨迹既要满足实际车辆换道轨迹形式,又要满足路径跟踪的特性.车辆在换道过程中的状态如图4所示.

图4 换道状态图

起始状态的参数通过传感器实时测量车辆状态获得,结束状态的参数根据换道目标进行设计,可以得到换道过程的边界条件为

(3)

式中:vo，vd分别为换道前、后车辆的纵向速度;w为车道宽度.

根据式(3)可知,车辆换道时纵向有5个约束限制,侧向有6个约束限制,因此分别选用四次多项式和五次多项式对纵横向运动进行描述[9],车辆换道轨迹函数为

(4)

式中：a0,a1,…,a4和b0,b1,…,b5为多项式系数;x(t),y(t)分别为纵向和侧向坐标.

为求解该多项式换道轨迹函数,将式(4)中多项式系数求解,转化为矩阵计算,令

a=[a4a3a2a1a0]T,b=[b5b4b3b2b1b0]T,

qx=[0vo0vd0]T,qy=[0 0 0w0 0]T,

则a=A-1qx,b=B-1qy,求解得到轨迹函数为

(5)

4 换道轨迹的优化

高速公路车道宽度w一般为3.75 m,在同向三车道的高速公路上行驶时,假设换道车辆M从中间车道以vo=28 m·s-1变道至左侧车道,换道结束时速度为vd=32 m·s-1.根据假设条件和式(5),可以求得此种情况下换道轨迹函数为

(6)

根据式(6)可知,整个换道轨迹函数只与换道时间tf有关.在对tf取值时,大多是根据经验进行给定,这极大降低了换道轨迹在复杂交通环境下的灵活性以及实用性.考虑到换道时车辆的侧向加速度ay对换道安全性、舒适性的影响以及换道时间tf对换道效率的影响.因此,建立以减小侧向加速度和换道时间为目标的规划函数J,从而对tf进行优化选取,该换道轨迹多目标规划函数为

(7)

式中:τ1,τ2为权重系数,且τ1+τ2=1.

τ1,τ2反映了在换道过程中对舒适性和换道效率的侧重性.而换道时,周围交通车辆状态决定了τ1,τ2的取值,当周围车辆与换道车辆的纵向距离较小时,不能考虑过多的舒适性,重点考虑换道效率;纵向距离较大时,可以重点考虑舒适性,从轻考虑换道效率.

根据V2V安全距离判断可知,车辆Lo,Ld,Fd和换道车辆M有潜在碰撞危险时,其中(sMLo(t0)/sMLo,sMLd(t0)/sMLd,sMFd(t0)/sMFd)最大一项反映了换道过程交通最为极限的状况,决定着权重系数τ2的取值,所以τ2=max(sMLo(t0)/sMLo,sMLd(t0)/sMLd,sMFd(t0)/sMFd),则τ1=1-τ2.

根据轨迹函数表达式,可以得到换道车辆侧向加速度ay随时间的变化关系,如图5所示.

图5 侧向加速度随时间的变化

从图5可以看出,换道时车辆侧向加速度幅值随着换道时间tf增加而减小.为了保证车辆安全完成换道,在对车辆换道时的安全换道距离提出要求时,还必须对车辆的侧向加速度ay加以控制,以防止车辆发生侧滑等横向稳定性失控问题,从而保障车辆在安全的前提下以较好的舒适性和较高的换道效率来完成整个换道过程.

根据汽车动力学可知,为了保证车辆在弯道或者转弯行驶时的横向稳定性,普通车辆的侧向加速度不宜超过0.4g[10],g为重力加速度,则有aymax=0.4g.

据统计车辆在高速公路平稳完成加速换道过程一般在5 s内完成,即认为tfmax=5 s.

约束优化模型为

(8)

在换道时刻,换道车辆通过V2V获得周围交通状况信息后,根据该优化模型确定换道时间tf,从而为车辆规划一条最优换道轨迹.

5 仿真分析

车辆在高速公路行驶,无突发状况时,可认为周围车辆都趋于匀速稳定的行驶工况.即换道时当前车道的前车Lo,后车Fo都以28 m·s-1的车速匀速行驶,目标车道前车Ld以及后车Fd以32 m·s-1的车速匀速行驶.车辆的车长L取4.2 m,车宽取1.8 m.由于目标车道前车Ld在换道过程中车速vLd大于车辆M的车速vM,只要保证在开始换道时与车辆M有车长L的安全换道距离时,即认为Ld对M的换道没有影响;而当前车道的前车Lo,目标车道的后车Fd与M的换道安全距离分别为

sMLo(t0)=3.0+4.2=7.2 m,

sMFd(t0)=10.0+4.2=14.2 m.

为了满足车辆在换道的安全距离要求,在开始换道时刻取sMLo=10.0 m,sMFd=20.0 m,根据上述结果可以求得

τ2=max{sMLo(t0)/sMLo，sMFd(t0)/sMFd}=0.72,

τ1=1-τ2=0.28.

利用迭代求解该优化问题，结果如图6所示,求得该交通状态下车辆的最优换道时间tf=2.7 s.

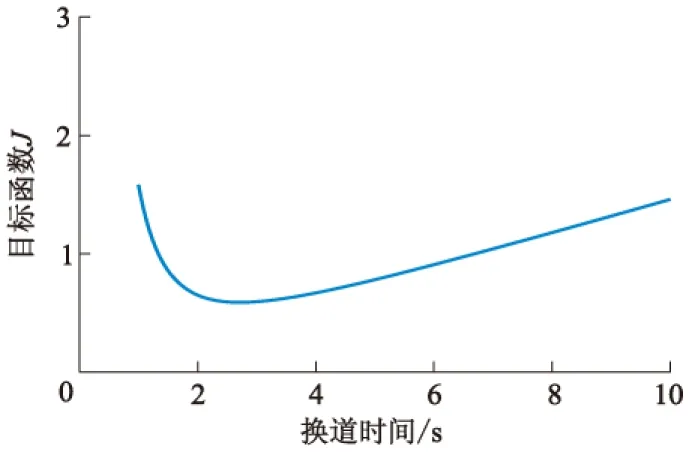
图6 目标函数曲线

车辆以不同换道时间tf从vo=28 m·s-1车道换到vd=32 m·s-1车道时的换道轨迹曲线如图7所示.图中显示的换道时间tf过短为车辆危险换道轨迹,而换道时间tf>5 s，虽然换道舒适性可以得到提高,但在实际换道过程，换道时间不宜过长.两者之间为车辆可行的换道轨迹,而通过对目标函数求解得到了权衡舒适性和换道效率的最优换道轨迹.

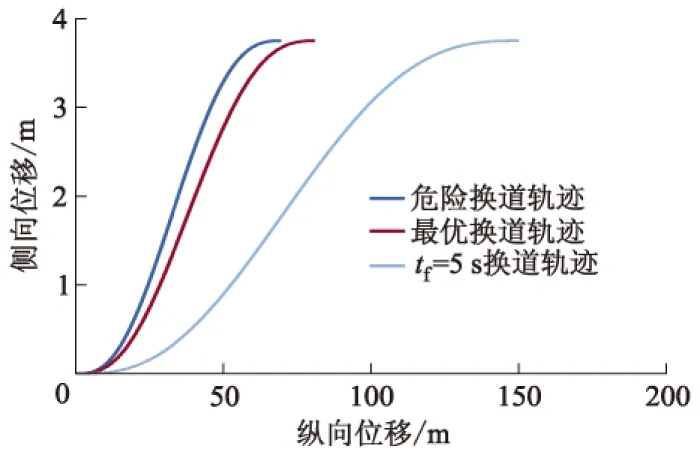
图7 换道轨迹函数曲线

而在相同的换道环境下,根据文献[11]中优化模型求解得到的最优换道时间为3.7 s,计算两种不同换道模型在相同场景下换道车辆M运行至道路中心线位置时与当前车道前车Lo距离,换道结束时刻与目标车道的后车Fd的距离,结果如表1所示.

表1 换道危险点时与各车距离表 m

通过计算,进一步得到了在同一换道环境下,基于V2V的换道模型与文献[11]换道模型中优化得到的最优轨迹如图8所示.

图8 不同模型的最优轨迹

从图8可以看出：由于V2V模型对换道轨迹中目标函数权系数的合理调整,在保证换道的安全性下,与交通车在危险碰撞点时所保持的距离更加充裕,而且换道的纵向位移也得到了缩减,进一步说明该V2V换道模型所规划的轨迹对交通环境具有更佳的适配性.

在CarSim中选取某款C级车进行换道动力学仿真,路面附着系数取为0.85,车辆的换道路径和速度规划通过MATLAB的数据导入.为了平稳进行换道,让车辆沿道路中心线直行0.5 s后进行换道,车辆换道场景如图9所示.

图9 车辆换道场景

通过CarSim仿真可以看出：基于V2V建立的车辆换道安全距离模型,可以保证车辆在整个换道过程中不与其他交通车发生碰撞,依据给定交通状态规划出来的轨迹可以满足整个换道要求.换道过程车辆动力学参数曲线如图10所示.

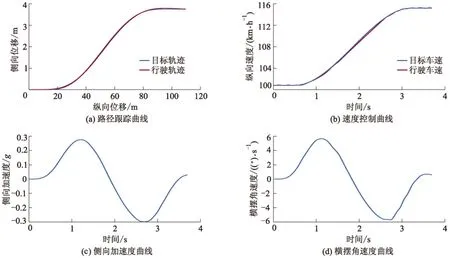
图10 车辆动力学参数曲线

从图10a,b可以看出:路径偏差和速度偏差都控制在极小范围内,该多项式规划出来的换道轨迹具有较好的跟踪效果.从图10c,d可以看出:车辆的侧向加速度与横摆角速度的变化在整个换道过程中十分平滑且控制在稳定行驶的范围内,所以换道过程中的舒适性可以得到满足.

6 结 论

1) 根据车辆的运行状态信息,建立了基于V2V的换道安全距离判断模型,避免换道过程车辆间发生碰撞.

2) 考虑换道前后的边界条件,以多项式函数来描述车辆的换道轨迹;相比匀速换道,考虑了车辆在换道过程完成车辆的加速,使得换道结束时车辆能够更快地融入车流中.

3) 建立了减小侧向加速度和换道时间的多目标规划函数,通过V2V获取周围交通状态,决定着舒适性和换道效率的权重取值,因此对换道时间进行最优选取,使得规划出来的轨迹能够适配该交通环境.