与多个数论函数相关的复合函数方程解的存在性
张明丽,高 丽*,张炳存,郭梦媛
(1.延安大学 数学与计算机科学学院,陕西 延安716000; 2.定边县第四中学,陕西 定边 718600; 3.陕西师范大学出版总社,西安 710000)
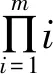
1 相关引理
引理1[2-4]由简数定理知:
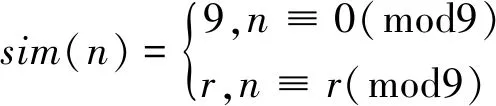
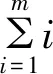
引理3[5]对任意素数p≥3,Z(p)=p-1.
引理4[5]对任意素数p≥3及k∈N+,Z(pk)=pk-1.当p=2时,则有Z(2k)=2k+1-1.
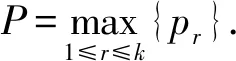
2 主要结论及其证明

证明对于混合函数方程:

(1)
的解主要分以下两种情形进行讨论:

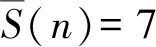

①对于α=7,p=3的情况,n=2s13s25s37s411s513s617s719s8(其中0≤s1≤10,s2=7,0≤s3≤4,0≤s4≤2,0≤s5,s6,s7,s8≤1),带入式(1)验证均符合,故此时式(1)有2 640个解为n=2s13s25s37s411s513s617s719s8(其中0≤s1≤10,s2=7,0≤s3≤4,0≤s4≤2,0≤s5,s6,s7,s8≤1).
②对于α=3,p=7的情况,n=2s13s25s37s411s513s617s719s8(其中0≤s1≤10,2≤s2≤6,0≤s3≤4,s4=3,0≤s5,s6,s7,s8≤1),带入式(1)验证均符合,故此时式(1)有4 400个解为n=2s13s25s37s411s513s617s719s8(其中0≤s1≤10,2≤s2≤6,0≤s3≤4,s4=3,0≤s5,s6,s7,s8≤1).
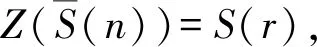


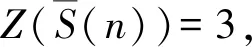
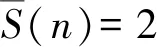
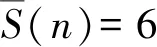
(i)对于α=3,p=2的情况,n=2s13s25s3(其中s1=3,0≤s2,s3≤1),共有4种组合,带入式(1)验证,此时符合式(1)的解共有2个,为n=24,120.
(ii)对于α=2,p=3的情况,n=2s13s25s3(其中0≤s1≤2,s2=2,0≤s3≤1),归于情形一,不再赘述.
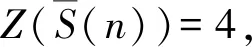

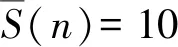
(i)对于α=5,p=2的情况,n=2s13s25s37s4(其中s1=5,0≤s2,s3,s4≤1),共有8种组合,带入式(1)验证,此时符合式(1)的解仅有n=1 120.
(ii)对于α=2,p=5的情况,n=2s13s25s37s4,(其中0≤s1≤4,0≤s2≤1,s3=2,0≤s4≤1)共有20种组合,带入式(1)验证,此时符合式(1)的解共有2个,为n=175,400.

①对于α=5,p=3的情况,对应有n=2s13s25s37s411s513s6(其中0≤s1≤7,s2=5,0≤s3,s4≤2,0≤s5,s6≤1),归于情形一,不再赘述.
②对于α=3,p=5的情况,对应有n=2s13s25s37s411s513s6(其中 0≤s1≤7,s3=3,0≤s4≤2,0≤s2,s5,s6≤1),共有192种组合,带入式(1)验证,此时符合式(1)的解共有16个,为n=1 625,6 125,2 750,500,250 250,45 500,77 000,700 700,14 000,1 274 000,572 000,2 156 000,104 000,392 000,176 000,16 016 000.
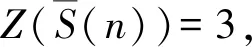

①对于α=2,p=2的情况,n=4,12,带入式(1)验证均不符合,故此时式(1)无解.
②对于α=7,p=2的情况,n=2s13s25s37s411s513s6(其中s1=7,0≤s3≤2,0≤s2,s4,s5,s6≤1),共有48种组合,带入式(1)验证,此时符合式(1)的解共有3个,为n=18 304,4 480,246 400.
③对于α=2,p=7的情况,n=2s13s25s37s411s513s6(其中0≤s1≤6,s4=2,0≤s3≤2,0≤s2,s5,s6≤1),共有168种组合,带入式(1)验证,此时符合式(1)的解共有14个,为n=637,35 035,1 078,6 370,350 350,196,10 780,63 700,1 960,107 800,19 600,224 224,40 768,2 242 240.
④对于α=14,p=2的情况,对应有n=2s13s25s37s411s513s617s719s823s9(其中s1=14,0≤s3≤5,0≤s4≤3,0≤s5,s6≤2,0≤s2,s7,s8,s9≤1),共有3 456种组合,数据进行筛选,符合式(1)的解共有288个(此处省略,对于具体数值不加赘述),即使得n的值同时满足如下两个条件:
(i)n=2s13s25s37s411s513s617s719s823s9(其中s1=14,0≤s3≤5,0≤s4≤3,0≤s5,s6≤2,0≤s2,s7,s8,s9≤1);
(ii)sim(n)=7.
⑤对于α=4,p=7的情况,n=2s13s25s37s411s513s617s719s823s9(其中0≤s1≤13,0≤s3≤5,s4=4,0≤s5,s6≤2,0≤s2,s7,s8,s9≤1),共有12 096种组合,对数据进行筛选,符合式(1)的解共有1 008个(此处省略,对于具体数值不加赘述),即使得n的值同时满足如下两个条件:
(i)n=2s13s25s37s411s513s617s719s823s9(其中0≤s1≤13,0≤s3≤5,s4=4,0≤s5,s6≤2,0≤s2,s7,s8,s9≤1);
(ii)sim(n)=7.
综上,满足定理1中给定混合数论函数方程的解有有限多个.
3 相关推论及其性质证明
推论对于任意的正整数n,若设n的标准分解式为n=p1α1p2α2…prαr(其中p1,p2,…,pr均为素数),则对于简数根函数sim(n)有:
sim(n)=sim(p1α1p2α2…prαr)=sim(sim(p1α1)p2α2…prαr)=…=
sim(sim(p1α1)sim(p2α2)…sim(prαr))=sim(sim(p1)α1sim(p2)α2…sim(pr)αr).
证明结合引理1,运用数学归纳法易证.
性质1sim(1i)=1(i∈N+).
性质2 对于2i,4i,8i及5i,7i(i∈N+),有:sim(2)=2;sim(22)=4;sim(23)=8;sim(24)=7;sim(25)=5;sim(26)=1;…;sim(26i+1)=sim(26i×2)=sim((sim(26))i×sim(2))=sim(2)=2;sim(26i+2)=4;sim(26i+3)=8 ;sim(26i+4)=7 ;sim(26i+5)=5 ;sim(26i+6)=sim((26)i)=1(其中i∈N+).
证明1)运用数学归纳法,对上述sim(26k)=sim((sim(26))k)进行验证.
①当k=1时,易知sim(26)=sim(sim(26))=sim(1)=1成立.
②假设k=i(i∈N+)时,sim(26i)=sim((sim(26))i)成立.那么,当k=i+1(i∈N+)时,有sim(26(i+1))=sim(sim(26i)sim(26))=sim(1×1)=1,命题得证.
2)sim(4)=4;sim(42)=7;sim(43)=1;sim(44)=4;sim(45)=7;sim(46)=1;…;sim(43i+1)=sim(43i×4)=sim((sim(26))i×sim(4))=sim(1×4)=4;sim(43i+2)=7;sim(43i+3)=sim((sim(26))i+1)=1(其中i∈N+).
3)sim(8)=8;sim(82)=1;sim(83)=8;sim(84)=1;sim(85)=8;sim(86)=1;…;sim(82i+1)=sim(82i×8)=sim((sim(26))i×sim(8))=sim(1×8)=8;sim(82i+2)=1;(其中i∈N+).
4)sim(5)=5;sim(52)=7;sim(53)=8;sim(54)=4;sim(55)=2;sim(56)=1;…;sim(56i+1)=sim(56i×5)=sim((sim(56))i×sim(5))=sim(5)=5;sim(56i+2)=7 ;sim(56i+3)=8;sim(56i+4)=4 ;sim(56i+5)=2 ;sim(56i+6)=sim((56)i)=1(其中i∈N+).
5)sim(7)=7;sim(72)=4;sim(73)=1;sim(74)=7;sim(75)=4;sim(76)=1;…;sim(73i+1)=sim(73i×7)=sim((sim(76))i×sim(7))=sim(7)=7;sim(73i+2)=4 ;sim(73i+3)=1 (其中i∈N+).
2)3)4)5)证明可参照(1)进行.
性质3 对于3i,6i(i∈N+),有:
1)当i=1时,sim(3)=3;当i≥2时,sim(3i)=9;
2)当i=1时,sim(6)=6;当i≥2时,sim(6i)=9.
证明同上易证.
例1 对于11i(i∈N+),要使sim(n)=7,则有:
sim(sim(11)×8)=sim(16)=7;
sim(sim(112)×4)=sim(sim(121)×4)=sim(4×4)=sim(16)=7;
sim(sim(113)×2)=sim(sim(1 331)×2)=sim(8×2)=sim(16)=7;
sim(sim(114)×1)=sim(sim(14 641)×1)=sim(7×1)=7;
sim(sim(115)×5)=sim(sim(161 051)×5)=sim(5×5)=sim(25)=7;
sim(sim(116)×7)=sim(sim(1 771 561)×7)=sim(1×7)=7;
…
sim(sim(116i+1)×8)=sim(16)=7;
sim(sim(116i+2)×4)=sim(4×4)=sim(16)=7;
sim(sim(116i+3)×2)=sim(8×2)=sim(16)=7;
sim(sim(116i+4)×1)=sim(7×1)=7;
sim(sim(116i+5)×5)=sim(5×5)=sim(25)=7;
sim(sim(116i+6)×7)=sim(sim(11)6i+6×7)=sim(26i+6×7)=sim(1×7)=7.

