一类环境受随机干扰的广告扩散模型的动力学分析
冯鹏鹏,李祖雄
(湖北民族大学 理学院,湖北 恩施 445000)
0 引言
日常生活中,商品的销量通常受到很多因素的影响,比如广告的投放、商品的口碑、商场的位置等.当商家推出一种新的商品时,商家需要对商品的销量进行预估,为了更好地预判商品的市场竞争力,研究者们借助数学工具建立适当的数学模型进行理论分析,用以帮助商家调整销售策略.文献[1-4]通过对广告模型进行分析得出了许多丰富的成果.
Feichtinger[5]研究了一种具有扩散效应的广告模型,如下:
(1)
其中X1代表了某品牌在t时刻的潜在购买者,X2表示该品牌在t时刻的购买者,假设在t时刻潜在消费者进入商场的输入率为常数k,那么潜在购买者的数量、当前购买者的数量以及时间区间这三者存在一个比率关系,这一关系简称为接触率,这里用α表示.同时,该品牌的购买者中也会有以β为比例转向对立品牌,由于他们以后还有可能购买该品牌,所以仍将他们归为潜在消费者.又假设当前的消费者里会有人以常数率ε永久离开(例如人口迁移或死亡),令δ=β+ε,就得到了模型(1).
对确定性模型(1)已经有许多学者进行了分析并得到了许多好的结果,然而实际生活充满了各种不确定性因素,人们在实际消费时并不总是理性的会受到很多因素的影响,如天气、路线等因素的影响,把这些影响人们消费的因素归为随机干扰,如果不考虑这些因素,得到的结果将会与实际有较大的出入.自从伊藤清提出了伊藤积分,人们有了解决随机微分方程的工具之后,随机微分方程的研究取得了突破性的进展并取得了丰硕的成果[6-8].基于环境因素的对消费者消费行为的影响,考虑到对模型(1)进行随机扰动,假设研究中的随机扰动与系统变量成正比,建立对应于研究性模型(1)的随机系统:
(2)
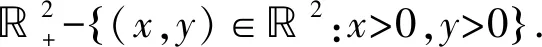
1 预备知识
本节给出本文中所需的相关定义、引理以及符号说明.
一个d维It型随机微分方程如下:
dX(t)=f(X(t),t)dt+g(X(t),t)dB(t),t0≤t≤T,
(3)
其初值为X(t0)=X0,随机微分方程(3)等价于下列积分方程:
(4)
定义1[7-9]如果X(t)具有如下的性质,则称d-值随机过程{X(t)}t0≤t≤T为随机微分方程(3)的解:
i) {X(t)}右连续,并且是Ft-适应的;
ii) {f(X(t),t)}∈L1([t0,T];d),且{g(X(t),t)}∈L2([t0,T];d×m);
iii) 对∀t∈[t0,T],方程(4)依概率1成立.
定义2[10](多维It公式)当t≥0时,假设X(t)是一个满足如下随机分为方程的d维It过程:
dX(t)=f(t)dt+g(t)dB(t),
其中g∈L2(+;d×m).令V∈C2,1(d×+;),那么V(x(t),t)仍然是It过程且满足随机微分方程:
2 全局正解的存在唯一性
为了研究随机模型(2)的动力行为,首先给出一条定理来确保模型(2)全局正解的存在唯一性.

证明证明借鉴文献[11-12]中的方法,虽然随机模型不满足Lipschitz条件,但是在变换后是满足局部Lipschitz条件的,也即对于任意给定的初值(x0>0,y0>0),模型在t∈[0,τe)上都存在着局部唯一解,这里τe是爆破时刻.如果能证明τe=,那么模型的解即是全局存在的.
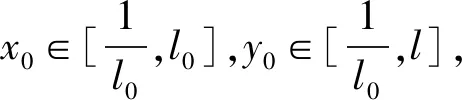
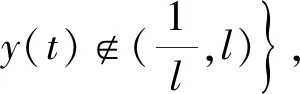
假设τ≠,那么存在一对常数T>0及ε∈(0,1),满足P{τ≤T}>ε.也就是说存在整数l1≥l0,使得,∀l>l1.定义如下的V函数:+,V(x,y)=(x-1-lnx)+(y-1-lny),由u-1-lnu≥0,可知V函数的正定性.由It公式可以得到:
其中:

又令C=(β-δ)yu+α(yu)2+k+δ,可得:
上式两边同时从0到τε∧T积分,并取期望得到:


由此可得:
(V(x0,y0)+CT)≥E[IΩl(ω)V(x(τl,ω),y(τl,w))]=
其中IΩε(ω)是Ωε的指标函数,令ε→0可得出矛盾.因此τ=,定理1得证.
3 模型解的渐近行为
本节将讨论当外部干扰(即σ1和σ2)过大时,系统的解将会表现出什么样的动力学行为,这里首先给出以下定理:

证明由文献[13]和模型(2)有d(x(t),y(t))=(k+(β-δ)y)dt+σ1xdB1(t)+σ2ydB2(t).令V(x(t),y(t))=ln(x(t)+y(t)),这里x(t),y(t)∈(0,),运用It公式得到:
(5)

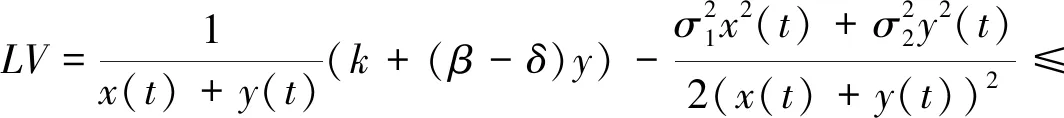

接下来考虑矩阵:
由定理2,如果条件满足,那么以上矩阵为负定矩阵,并且其具有最大特征值λmax(负的),于是有:

将其带入到(5)得到:
对上面不等式的两边同时积分,并且结合Brownian运动的强大数定律:

因此,随着t→,x(t)→0且y(t)→0 a.s.
注1 定理2得到了一个有趣的结论,可以看到当外界的随机扰动的强度足够大时,潜在购买者和购买者都将以概率1指数趋于0,这说明外界环境产生的随机性干扰确实会使对消费者的购买行为产生很大的影响,随机动力学模型表现出与确定型模型不一样的动力学行为.
4 结语
本文考虑了一类受到随机环境扰动的具有扩散效应的广告模型,研究的重点放在了当外部干扰强度足够大,这时会对原来的系统产生较大的影响.如果在模型(2)中考虑加入时滞的影响[14],该模型会更加接近实际情况,但是会增加研究难度,在未来的工作中会考虑这一问题.

