捕获率对一类捕食-食饵模型的影响
卓义峰,慕 嘉
(西北民族大学 数学与计算机科学学院,兰州 730030)
近年来,随着人类对自然界的越发重视,许多学者都投入到种群生态学的研究.在文献[1-3]中,学者用捕食者-食饵模型来描述在一个特定的生态系统中多个种群随时间的变化.而在实际应用中,生态系统的特性往往还受到许多其他因素的制约,如文献[4]中的Allee效应,文献[5]中的时滞对生态系统的影响,等.此外,若捕食者或者猎物中产生了疾病,也会对整个生态系统产生巨大的影响[6-14],针对不同的生态系统,本文分别用SI模型、SIS模型、SIR等模型来描述不同情况下传染并对生态系统的影响.本文根据已有的工作,建立模型并求解.
1 模型的建立
考虑文献[7]中的具有Holling II型功能反应函数的Rosenzweig-MacArthur捕食-食饵模型:
(1)
其中,N和P分别表示随着时间t变化的食饵和捕食者的种群密度,b是猎物种群的平均最大生育率,di(i=1,2,3)分别是猎物和捕食者的死亡率,α表示猎物种群内部竞争的强度,s表示有效搜索率,h表示处理时间,c表示捕食猎物转换为新的捕食者的转换效率.
在模型(1)的基础上,并从经济效益的角度考虑,对未染病的食饵种群以及捕食者种群加入线性收获项[15]得到系统(2):
(2)
其中h1,h2表示捕获率,因为I是感染者,从捕获效益上考虑不进行捕获.为考虑食饵染病的情况,做出如下假设.
i) 当猎物N受到感染后,物种由未感染者(N)和感染者(I)组成.在t时刻有:N(t)=H(t)+I(t).
ii) 感染后的猎物因较高的死亡率(设死亡率为d2)以及行动不便而被捕食而不考虑繁殖功能,因此只考虑未感染者H的繁殖能力.

2 模型分析
2.1 解的有界性
定理1 系统(2)的解在初始条件下一致有界的.

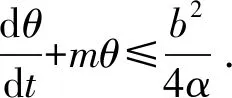
当t→时,所以在中,系统的解是一致有界的.
2.2 平衡点的存在性
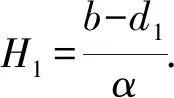
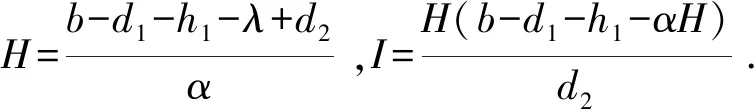
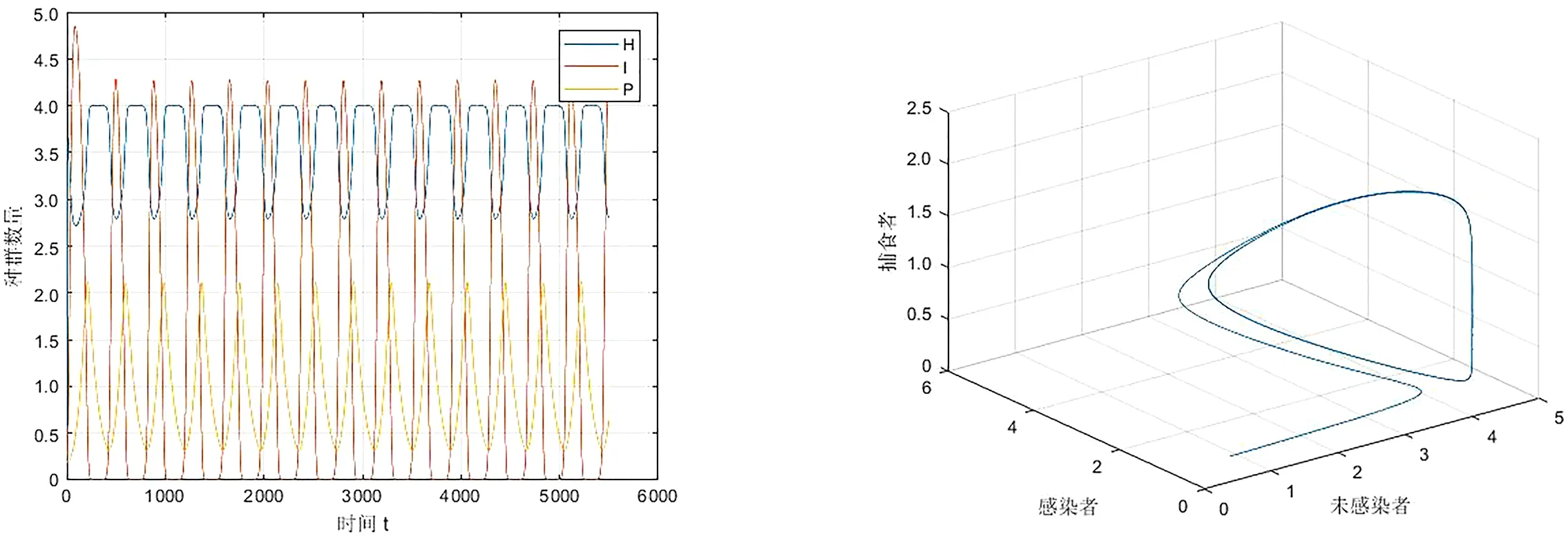
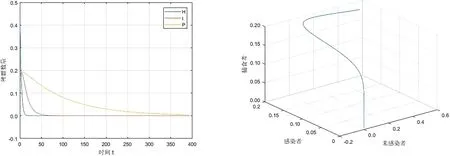
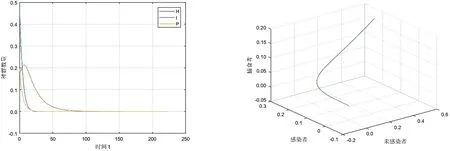
结合上式,当d2<λ αH*2-(b-d1-h1-αI*)H*-(b-d1-h1-λ)I*=0 (3) 现在令αH*2-(b-d1-h1-αI*)H*-(b-d1-h1-λ)I*=f(x),为了让式(3)有正根,需要满足当f(x)<0且Δ>0,即: Δ=(b-d1-h1-αI*)2-4α(b-d1-h1-λ)I*>0,-(b-d1-h1-λ)I*<0. 系统(2)的Jacobi矩阵为: 2.3.1 平衡点E0(0,0,0)的稳定性分析 系统(2)的平衡点E0(0,0,0)的Jacobi矩阵JE0为: 那么,矩阵JE0的特征根为b-d1-h1,-d2,-d3-h2.可知,若b 2.3.2 平衡点E1(H1,0,0)的稳定性分析 系统(2)在平衡点E1(H1,0,0)的Jacobi矩阵JE1为: 那么,矩阵JE1的特征根分别为d1+h1-b,λ-d2,-d3-h2.若b 2.3.3 平衡点E2(H2,I2,0)的稳定性分析 对于平衡点E2(H2,I2,0),考虑如下系统: (4) 显然,系统(4)的正平衡点E1′=(H2,I2)且系统在点E1′=(H2,I2)的Jacobi矩阵J2为: J2的特征方程为:A2-TA+D=0. 当满足d2<λ detJ2′=b11b22-b12b21= 即Jacobi矩阵J2′的特征根有负实部,系统(4)的平衡点E1′=(H2,I2)是局部渐进稳定的,那么,在满足相同条件下,系统(2)在E2(H2,I2,0)也是局部渐进稳定的. 2.3.4 平衡点E*(H*,I*,P*)的稳定性分析 证明系统在平衡点E*(H*,I*,P*)的Jacobi矩阵为: 其中: 矩阵J*的特征方程: ξ3+A1ξ2+A2ξ+A3 (5) 其中: A1=-(a*11+a*22) , A2=(a*11a*22-a*12a*21)-(a*23a*32+a*13a*31) , A3=(a*13a*31-a*12a*23)+(a*11a*23-a*13a*21)a*32. 为使方程(5)的所有根都具有负实部,根据Routh-Hurwite判据,行列式L应满足: (6) (7) 则满足a*11<0,a*22<0即A1>0.结合式(6)、(7)的条件,矩阵J*中的元素就可以整理如下: a*11<0,a*12<0,a*22<0,a*23<0,a*21>0,a*32>0, 显然有A1A2-A3>0. 下面证平衡点E*(H*,I*,P*)全局渐进稳定: A(H-H*)2+B(H-H*)(I-I*)+C(I-I*)2+D(I-I*)(P-P*) . 即平衡点E*(H*,I*,P*)全局渐进稳定. 定理3 当d2=d2*,系统(2)在正平衡点E*(H*,I*,P*)产生Hopf分支. detJ*=a*11a*22a*33-a*12a*21a*33-a*11a*23a*32, 根据行列式中各个元素的正负,可得到detJ*>0. 为了研究该模型的生物意义,通过计算机对该模型进行数值模拟.根据模型的生物意义,以模型的线性捕获率为控制量对其进行分析b=0.6,d1=0.2,α=0.1,λ=0.2,s=0.15,d2=0.06,d3=0.01,c=0.2,令h1=h2=0,系统(2)的时序图和相图如图1、图2所示. 图1 h1=h2=0时的时序图 图2 h1=h2=0时的相图Fig.1 Time series diagram for h1=h2=0 Fig.2 Time series diagram for h1=h2=0 从图1、图2可以看出系统(2)产生了周期解(极限环).现在保持其他条件不变,只改变最大生育率b=0.3,得到图3、图4. 图3 h1=h2=0时的时序图 图4 h1=h2=0时的相图Fig.3 Time series diagram forh1=h2=0 Fig.4 Time series diagram for h1=h2=0 从图3、图4可以看出系统(2)稳定.在图3、图4的原条件基础上,只改变捕获率h1=0.3,得到图5、图6. 图5 h1=0.3,h2=0时的时序图 图6 h1=0.3,h2=0时的相图Fig.5 Time series diagram for h1=0.3,h2=0 Fig.6 Time series diagram for h1=0.3,h2=0 从图5、图6不难发现,系统的整体变化不是很大,还是稳定的. 图7 h1=0,h2=0.3时的时序图 图8 h1=0,h2=0.3时的相图Fig.7 Time series diagram for h1=0,h2=0.3 Fig.8 Time series diagram for h1=0,h2=0.3 现在再从图3、图4的条件基础上,只改变捕获率h2=0.3,得到图7、图8,可以看出系统还是稳定的. 图9 h1=h2=0.2时的时序图 图10 h1=h2=0.2时的相图Fig.9 Time series diagram for h1=h2=0.2 Fig.10 Time series diagram for h1=h2=0.2 最后再保持图3、图4的条件不变,只改变捕获率h1=h2=0.2,得到图9、图10(见下页),可以看出系统还是稳定的.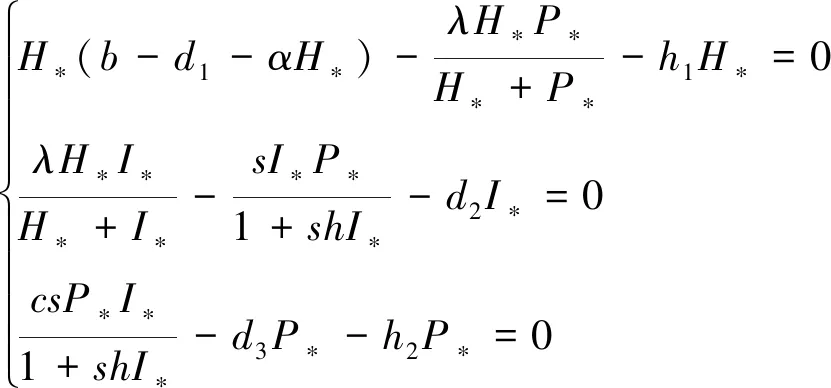

2.3 平衡点的稳定性



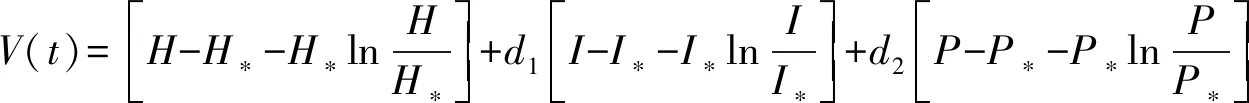

2.4 Hopf分支存在分析

3 数值模拟