基于SOLO分类理论的数学学习评价（一）——小学生“找出较复杂图形中梯形”的思维层次分析

□邵 虹

一、问题的提出

“图形与几何”是小学阶段数学课程的重要内容，几何知识的学习不仅对学生数学思维的开发起到积极作用，而且对学生核心素养的形成与发展有直接的影响。然而，“图形与几何”领域一贯以来又都是学生学习的难点，影响学生学业成就的主要因素与几何概念理解模糊、几何思维水平发展不足息息相关。

2018 年10 月，浙江省中小学教育质量监测中心对全省各县（市、区）的小学实施了大规模的监测；2019年6月公布了小学数学四年级监测的分析报告。其中，“图形与几何”领域测试得分率最低的是选择题第5题——“找出较复杂图形中的梯形”。这是一道情境变式题，需要学生在对梯形概念有深度理解的基础上，进行应用判断，有较高空间观念和空间推理能力的要求。

图1 2018年浙江省小学数学教育质量监测卷（第5题）[1]

测试数据显示，在36009 人的抽测样本数中，正确答案（C 选项）的选中率只有17.4%，而其他三个错误选项却高达25.3%、53.2%和3.9%。面对这样的结果，我们不得不反思几何概念教学中的缺失，但同时我们也存在一些疑惑：①学生解决问题时，对哪一种梯形的识别率比较高？②学生识别与判断梯形的依据是什么？③影响学生正确判断的因素有哪些？④学生解题时表现出来的几何思维层次是怎样的……由于此题是选择题，我们只能得到学生做出选择的结果，而对于学生解题时所表现出来的策略和思维过程却不得而知。为了更好地显现学生的解题过程、了解几何概念教学质量、分析几何思维水平的基本情况和存在问题，笔者决定改变此题的呈现方式，对学生进行测试和分析，以期为改进几何概念教学提供一些参考。

二、研究的设计

（一）研究对象

根据现行小学数学教材，四年级及以上年级的学生已经学过梯形的概念，能对一般四边形和特殊四边形进行整理和分类。因此，笔者选择了本区域（使用同一版本的小学数学教材）四年级学生96人作为研究对象。

（二）测试内容

为充分展示解题过程，分析学生的思维层次，本次测试改变了原题的问答方式，通过开放性的问题解答题展开实证研究。

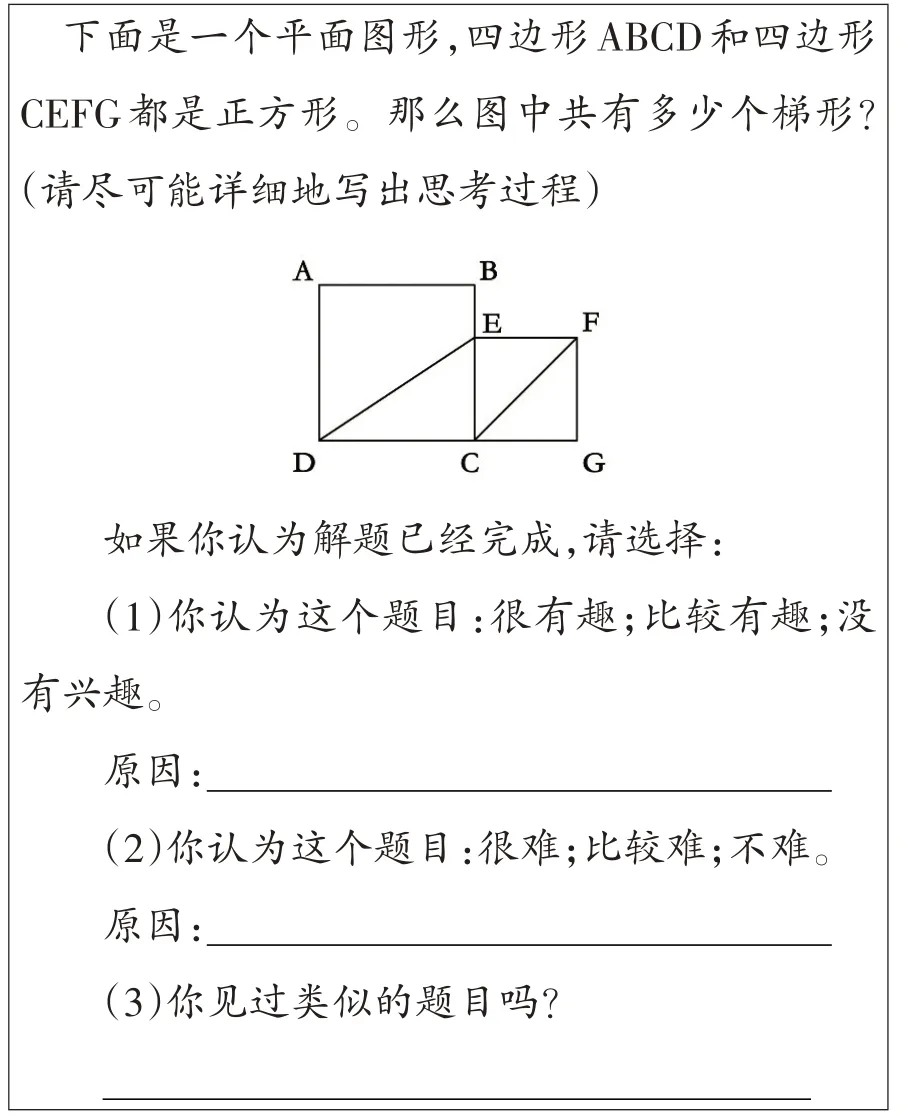
图2 学生“找出较复杂图形中的梯形”测试问卷

（三）评价工具

本研究主要参考SOLO 分类理论五种水平层次的划分确定能力框架。SOLO 是“观察到的学习结果的结构”（Structure of the Observed Learning Outcome）的缩写，由澳大利亚学者Biggs 和Collis（1992）所创。SOLO分类理论是在皮亚杰认知发展阶段论的基础上建立起来的。为确定复杂的学习过程层次提供了一个通用的框架，是一种以等级描述为特征的质性评价方法。[2]SOLO把题目的抽象程度和解决问题的复杂程度分为五种水平（或结构），分别是前结构水平、单点结构水平、多点结构水平、关联结构水平和抽象扩展结构水平。SOLO分类理论五种思维水平反映了学生的学习从量变到质变的过程，清晰、合理地解释了层次之间的递进！[3]从前结构水平到多点结构水平主要反映学习水平的量变，从多点结构水平到关联结构水平主要反映学生水平质的飞跃,从关联结构水平到抽象扩展水平预示着学习水平已经进入一个更高层次的思维水平。[4]

三、研究的结果

本研究对来自不同学校的四年级学生作答表现进行统计，其中S小学32人、F小学31人、M小学33 人，合计96 人。后继将分析同一学校不同年级学生的作答表现，分别是S小学五年级39人和六年级40人。根据SOLO分类理论，笔者针对学生的思维水平层次性和差异性进行分析。

（一）四年级学生的总体表现

四年级测试的样本数为96 人，能正确找到三个梯形的有26 人，约占总人数的27.1%，不能完整解答或解答错误的有70 人，约占总人数的72.9%。由于本次测试要求学生写出解题过程，因此学生对“哪种梯形的识别率高？哪种梯形的识别率低？”就显而易见了。

表1 四年级学生“找出较复杂图形中梯形”的情况统计

从表1可知，学生从复杂情境中识别梯形的能力较弱。此外，题目隐藏的三个梯形中，梯形ABED 的识别率最高，共86 人，约占四年级测试总人数的89.6%；梯形DEFC 的识别率最低，只有33人，约占总人数的34.4%。找到两个梯形的48名学生中，正确识别梯形ABED的达到100%；而剩余的图形以梯形DEFG 居多，找到的学生有41 人；找到梯形DEFC的只有7人。

（二）SOLO分类评价的层次划分

基于以上数据，我们对学生“找出较复杂图形中的梯形”的结果有了进一步了解。但是，对学生数学学习的质性评价不仅仅要关注结果，还需要关注认知过程，需要建立思维能力培养的层次。而SOLO 分类理论，就是针对学生解决某一个具体问题时的表现，通过描述分析学习结果在思维结构上的复杂程度，反映学生从“量变”到“质变”的过程。因此，SOLO 分类为学习质量评价提供了重要的理论依据。

研究发现，学生找出梯形的个数不能简单地等同于思维层次的划分，注意点应放在学生对问题的解决过程和思维结构上。经过反复实践调整，笔者对SOLO 分类的五种思维水平进行了次层次的分类，并从能力、思维操作、一致性与收敛、应答结构四个方面制定了评价框架。[5]层次划分与描述如表2所示。

表2 描述了SOLO 五种水平层次的重要特征。其中，能力是指不同水平所需要的工作记忆量或注意的广度。思维操作，是指把数学信息、线索与结果联系起来的一种方式。一致性与收敛，分别是指数学信息与得到结果之间是否存在矛盾以及获得答案的数量。应答结构，以图示的形式表示上述的特点，其中×表示不相关的信息和素材，●表示已经向学生展示过的相关素材，○表示没有向学生提供过的素材或者原理。[6]

（三）四年级学生思维层次分析

依据SOLO 分类五种思维水平的次层次水平划分和描述，笔者对四年级学生解决此题的思维层次做了进一步的统计，如表3所示。

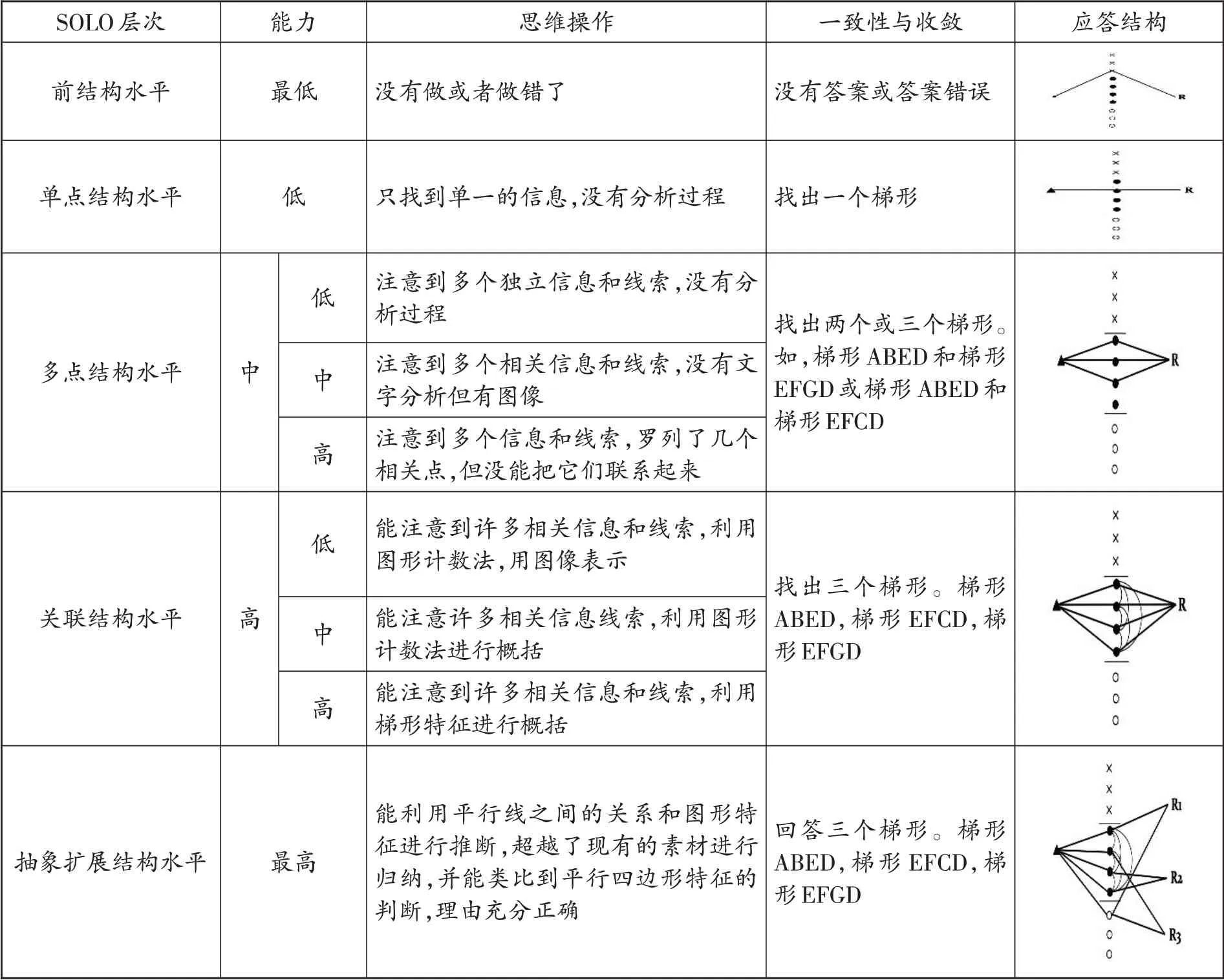
表2 SOLO分类五种思维水平的次层次水平划分和描述

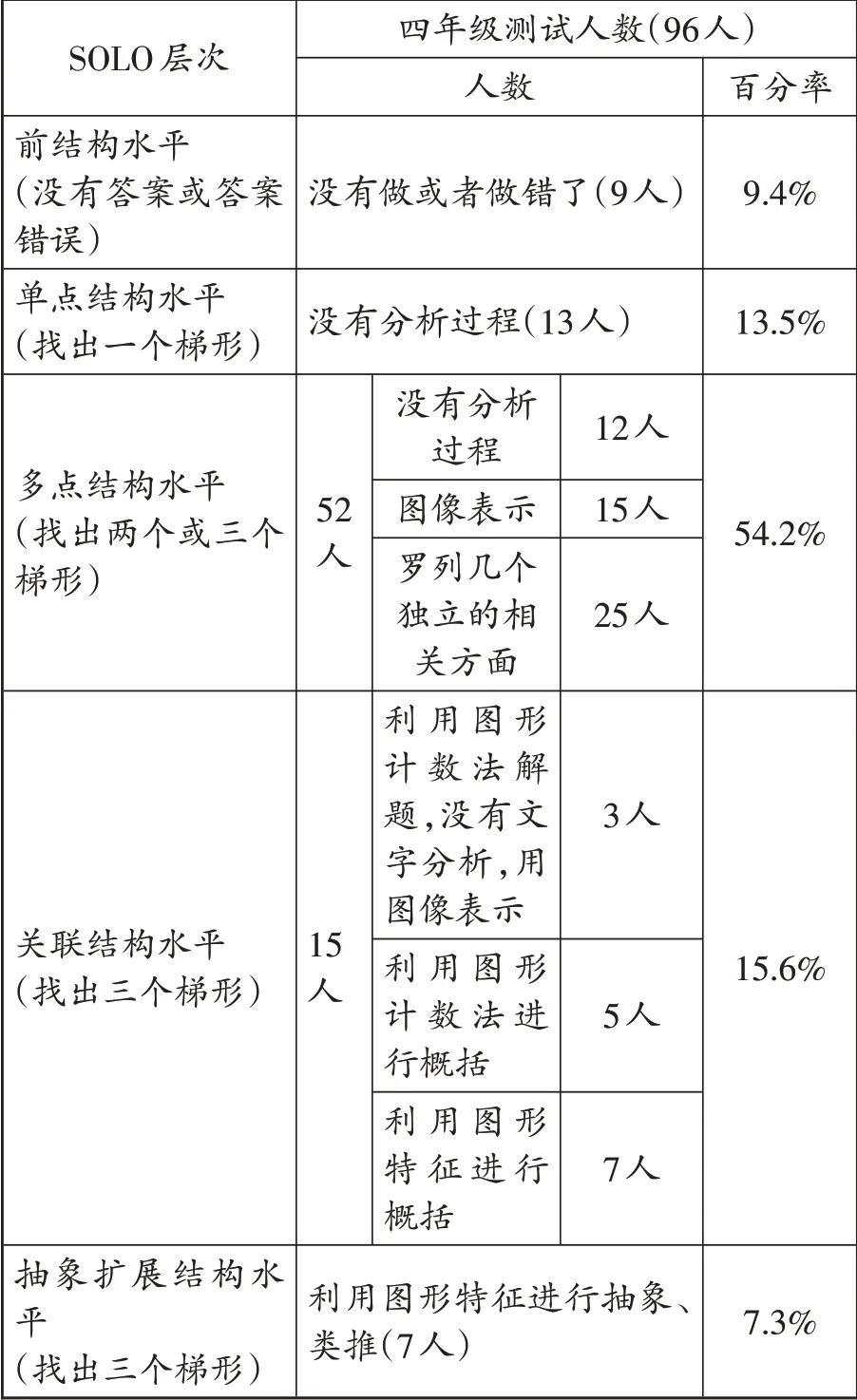
表3 四年级学生“找出较复杂图形中的梯形”SOLO分类的层次分析

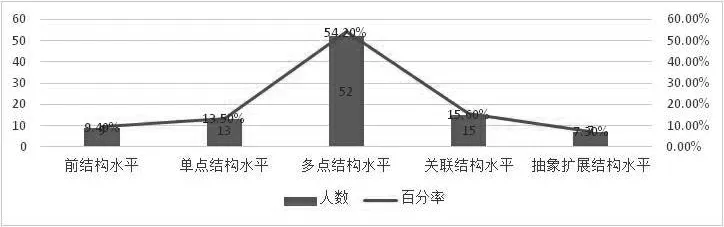
图3 四年级学生“找出较复杂图形中梯形”SOLO分类的层次分析

从图3的折线统计图可见，多点结构水平人数最多，约占四年级测试总人数的54.2%，其余水平以多点结构为中轴，向两侧逐渐降低，呈正态分布。大部分学生处于水平2 向水平3 过渡的阶段，即从单一信息的获取向多个信息过渡。学生在水平4和水平5 表现不佳，主要原因是：①学生对梯形特征的本质理解和掌握水平较低，多数学生只能注意到零散线索，以直观判断为主。②学生对梯形的整体感知能力薄弱，缺乏从较复杂的图形中分解出基本图形的能力和相应的经验。③无法有效地将图中梯形按结构分类，对共同特征进行归纳，并一类一类地进行有序表达。其次，面对思维水平稍高的情境题，部分学生不理解题意，不能迅速联想到解决问题所需的几何概念和性质，缺乏解题策略。

（四）学生典型作答的分析

在对学生的测试卷进行批改和统计后，笔者选取了不同水平的典型作答情况，分析学生的思维水平层次。

1.前结构水平：这部分学生主要表现为不理解题意和要点，拒绝作答或给出错误答案。四年级被测试学生中，有3 人卷面上直接写着“不知道”，拒绝回答是不想动脑的表现，从一个侧面说明他们没有积极地投入到学习和解题中。其余学生试图得出一个结果，但因未能找到相关联的知识逻辑，只能胡乱作答。

2.单点结构水平：这部分学生只能通过单一的信息，找出一个梯形。如图4 所示，根据梯形的外形特征，四个角和四条边直观判断。而四个角和四条边是所有四边形的基本要素而非梯形的独有特征；或通过“正方形—三角形”的剩余部分，从形的直观判断梯形。

图4 单点结构水平典例

3.多点结构水平：处于这一水平层次的学生人数最多，约占四年级测试总人数的54.2%。主要有三种表现：①没有分析过程，直接得出两个梯形的结果；②没有文字分析，用图像表征出两个梯形；③有一些零散、独立的文字分析，得出两个梯形的结果。这类回答中包含两个或多个与梯形有关的信息和线索，用到一定的记忆容量和注意广度，属于中等能力。但遗憾的是，这一水平层次的学生并没能将各相关信息联系起来，作为判断梯形的有力依据。如图5 所示，从多点结构水平典例一（1）右侧的草图可知，学生已经在头脑中建立了梯形的空间表象，知道梯形有且只有一组对边平行的属性，但是不能用数学语言进行描述。同时，从单个基本图形到多个组合图形的寻找过程，反映出学生尝试使用图形计数策略的痕迹。在多点结构水平典例一（2）中，学生同样罗列了一些信息和线索。与单点结构不同的是，该学生注意到了梯形的多个相关线索——上底、下底、两条斜线，但是没有联结这些信息，将上底和下底转化为“一组对边平行”的本质属性。

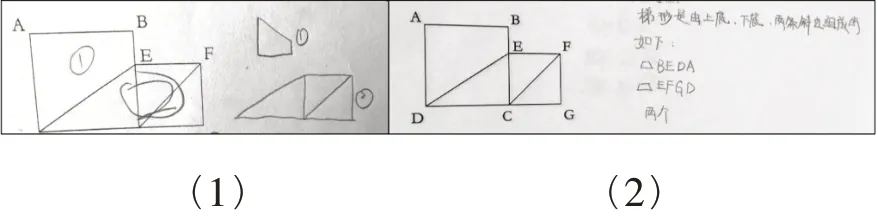
图5 多点结构水平典例一

此外，根据表1 统计发现，找到两个梯形的48名学生中，正确识别梯形ABED的达到100%；而剩余的图形以梯形DEFG 居多，找到的学生有41 人；找到梯形DEFC 的只有7 人。从另一侧面反映，学生对直角梯形辨识度高，他们头脑中的一般梯形大都是“一组对边平行，另一组对边是方向相反的两条斜边”，而梯形DEFC 更像是平行四边形，如图6所示。

图6 多点结构水平典例二

4.关联结构水平：处于这一水平层次的学生有15人，仅占四年级测试总人数的15.6%。主要表现为：①利用图形计数策略解题，没有文字分析，用图像表示；②利用图形计数策略进行概括，有具体的分析过程；③利用梯形的特征进行概括，有具体的分析过程。这类关联结构的回答进一步将多个线索联系起来，能用归纳的方式解释多点结构中零散、独立的信息，利用已有的知识、具体的经验，将相关知识联结成一个结构，用以解决问题。关联结构水平的学生中，有8人采用了图形计数的策略解决问题。如图7所示，学生按照“基本梯形、二合一梯形、三合一梯形”有序地寻找和判断。同时，还指出四边形ABED 和DEFG 是两个直角梯形，进一步说明学生对梯形中直角的强刺激和高辨识度。从对梯形DEFC的判断依据看，学生直观感知到其与平行四边形的差异，用另一组对边不相等的条件来进行证明，但未能触及最本质的区别。

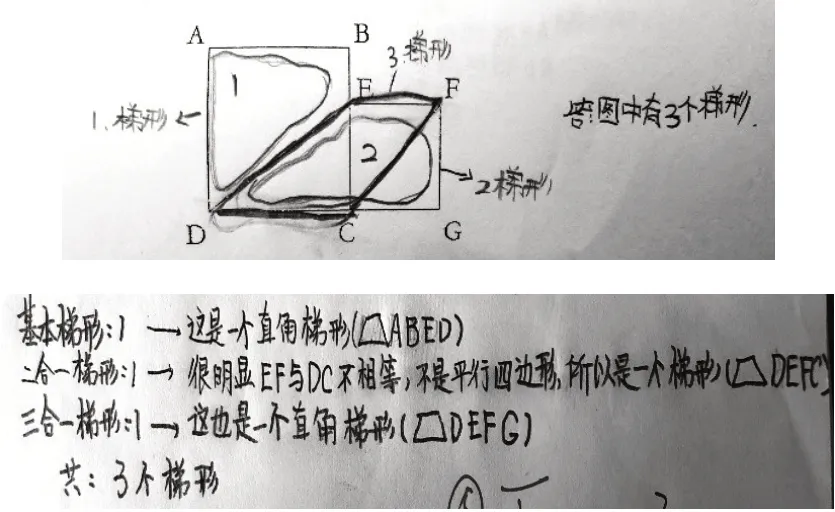
图7 关联结构水平典例一

处于关联结构水平的学生中，另有7人根据梯形的概念进行判断和证明。如图8所示，学生首先回顾了梯形的概念，而后根据题目给出的“四边形ABCD和四边形CEFG都是正方形”的线索，分析找出几组相互平行的线段——AD∥BC，BE∥AD，EF∥DG，AD∥FG。最后得出，平行线为横向的有梯形EFCD 和梯形EFGD，平行线为纵向的有梯形ABED。同理，另一位学生也是通过“有且只有一组对边平行”的属性进行概括与判断。以上几种表现，能将知识联结成一个体系，属于高认知思维水平，但还是只局限于已经教过的知识。

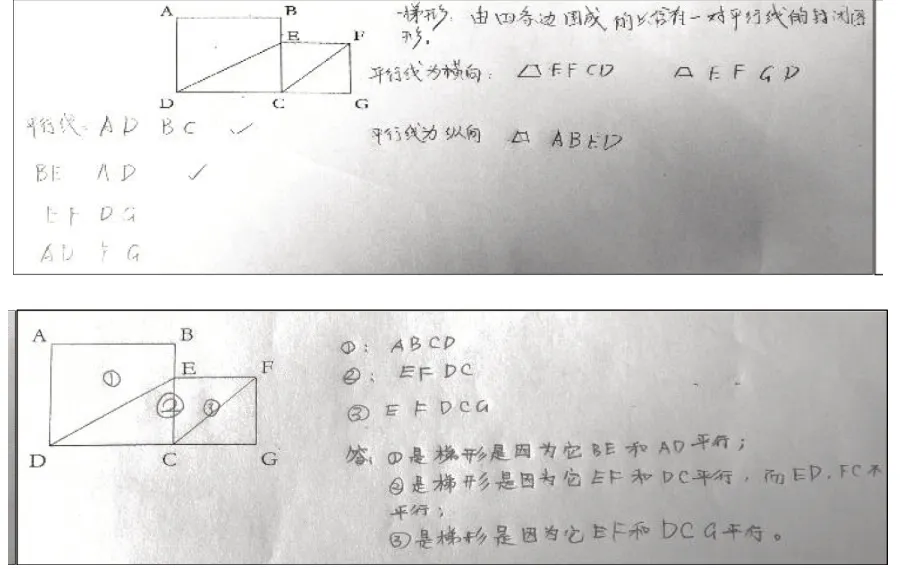
图8 关联结构水平典例二

5.抽象扩展结构水平：达到这一思维水平的学生，不仅能正确找到三个梯形，还能利用平行线之间的关系和图形特征进行推断，超越了现有的素材进行归纳，并能类比到平行四边形特征的判断，理由充分正确。显然，抽象扩展结构所需的工作记忆量或注意的广度比其他SOLO 分类层次的都要大。如图9 所示，学生从边与边的位置关系抽象出概念、原理，并对素材进行一一检验，从而得出结论。“因为BE∥AD，AB 不平行ED，为四边形，故四边形ABDE 为梯形”，推理过程已经拓展到了梯形的判定定理：一组对边平行，另一组对边不平行的四边形是梯形。这类学生的思维过程完整、清晰、简捷、合乎逻辑，将所有相关线索和它们之间的关系建立起一个抽象的普遍存在的原理，并能逐一证实这种假设的正确性和适用性。这样的表现，属于最高层次的认知思维水平。

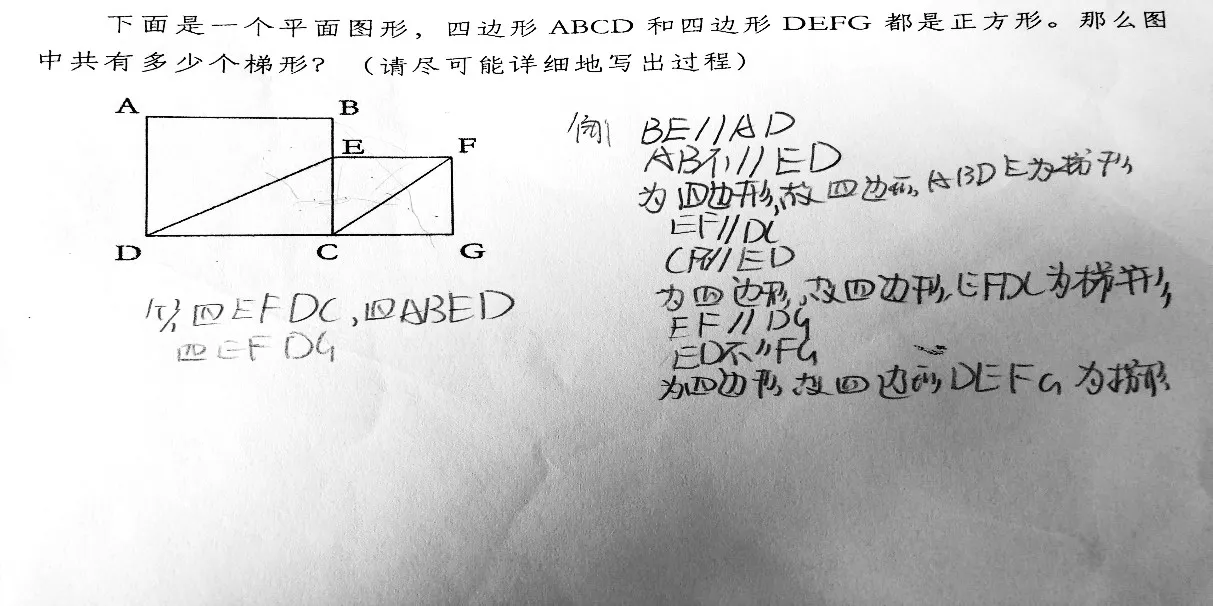
图9 抽象扩展结构水平典例一

研究发现，有个别学生已经能超越现有的线索和素材，将关联的知识结构概括到一个更高的抽象水平。如图10所示，学生不仅能识别梯形，还能与邻近几何概念进行比较，从而得出正确的结果。学生通过证明AD∥BE，而AD≠BE，判定四边形ABDE是梯形，也就是同一组对边平行且不相等的四边形是梯形。这类学生不仅深度理解了梯形的概念，还将概念拓展到梯形与平行四边形的判定定理上。笔者对这类学生进行了访谈，他们认为“这道题既考查观察能力，又把梯形的概念设计进去”“这道题考查了梯形和平行四边形的概念和区别”。由此可见，这类学生的思维反应呈现一致性、整体性和抽象性，属于最高层次的认知思维水平。

图10 抽象扩展结构水平典例二

很显然，抽象扩展结构水平的回答，不是多点结构水平的死记硬背概念和细节，也不是关联结构水平的简单重复，而是学生在对知识深度理解的基础上，自我建构逻辑体系，是量变到质变的飞跃。

此外，研究还发现，测试题目的趣味性、难易度和答题的正确率之间有着密切的关系。

表4 四年级学生题目的趣味性、难易度和答题的正确率统计

从表4 可知，约84.4%的四年级学生认为此题有趣或比较有趣。访谈时有的学生说第一次碰到这样的题目，有挑战性；有的学生认为这样的题目可以考考眼力和智商；还有的学生说“它用很巧妙的方法画出了几个梯形，找起来很有趣”。

另一方面，从表4 可知M 小学有54.6%的学生认为此题不难，但实际答题正确率只有24.2%。说明学生在解决开放性问题时容易入手，容易得到部分结果，但是忽略了题目要求是找到所有的梯形。F 小学有19.4%的学生认为很难，22.5%的学生认为比较难，这与他们答题正确率低有很大的相关性。S 小学有68.8%的学生认为很难或比较难，访谈时他们认为“这种复杂的图形，让我找出全部很难”“很容易看错、多找或少找了图形”“有部分线条比较乱，很难让眼睛无视无用的线条”……事实上，如果没有深刻理解梯形的概念，不能有序地思考问题，要找出所有梯形并详细写出思考过程是有一定难度的。

（未完，待续）