高考考查函数图象的三个视角

廖永福

(福建省厦门第二中学 361009)

函数是高中数学的重要内容，函数图象是函数的直观表示，是揭示函数性质的有力工具，是数形结合的重要载体，也是高考的热点之一.高考考查函数图象的试题一般从三个视角命制：函数图象的绘制、函数图象的识辨和函数图象的应用.考查形式多为选择题或填空题，难度基础或中等，常用特殊点法、排除法、数形结合法等解决.下面以近几年高考全国卷为例阐述如下：

一、函数图象的绘制

函数图象的绘制是高考的基本要求.已知函数的解析式，作函数图象一般有两种方法：描点法和图象变换法.当已知函数是基本函数时，可根据函数的特征找出图象的关键点直接作出图象；含有绝对值符号的函数，可去掉绝对值符号，化为分段函数后再作出图象；若函数可由某个基本函数的图象经过平移、翻折、对称得到，则可利用图象变换作出，对不能直接找到基本函数的要先变形，注意变换的顺序对变换单位和解析式的影响.

1.描点法

例1(2016年新课标Ⅰ)已知函数f(x)=|x+1|-|2x-3|．

(1)在图中画出y=f(x)的图象；

(2)求不等式|f(x)|>1的解集．

分析(1)利用绝对值的性质化简函数解析式，再画出函数的图象；

(2)根据图象写出不等式的解集.

(2)由|f(x)|>1，可得f(x)<-1或f(x)>1

点评本题考查分段函数图象的画法和绝对值不等式的解法，考查运算能力，属于基础题．

2.图象变换法

点评本题考查三角函数图象的变换，考查诱导公式的应用，考查运算能力．

二、函数图象的识辨

函数图象的识辨是高考的热点.一般有两种类型：知式选图和知图求式.前者是给出函数的解析式，确定所给函数的图象；后者是给出函数的图象,确定图象对应的函数解析式.解题的关键是从图象中读出有用的信息,并与函数解析式相互印证，进而解决问题.

寻找函数图象与解析式之间的关系，常从以下几个方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置；(2)从函数的单调性，判断图象的变化趋势；(3)从函数的奇偶性，判断图象的对称性；(4)从函数的周期性，判断图象的循环往复等.反之亦然.

利用上述方法排除错误选项，筛选正确选项.当选项无法排除时，可代特殊值，或从某些量上找突破口.

1.知式选图

例3 (2016新课标)函数f(x)=2x2-e|x|在[-2,2]的图象大致为( ).

分析通过研究函数的奇偶性、单调性、极值和特殊值，确定函数的图象.

解答函数f(x)=2x2-e|x|在[-2,2]上是偶函数，其图象关于y轴对称.

因为f(2)=8-e2∈(0,1)，故可排除A,B.

设g(x)=2x2-ex，则g′(x)=4x-ex.

∵g′(0)<0,g′(2)>0,∴g(x)在(0,2)内至少有一个极值点，

∴f(x)=2x2-e|x|在(0,2)内至少有一个极值点，排除C.故选D.

点评本题主要考查函数图象的识别和判断，利用导数研究函数的单调性和极值是解决本题的关键．

例4 (2015年新课标Ⅱ)如图,长方形的边AB=2，BC=1，O是AB的中点,点P沿着边BC，CD与DA运动,记∠BOP=x,将动点P到A，B两点距离之和表示为x的函数f(x),则函数的图象大致为( ).

分析解决此类问题可以根据已知条件求出函数解析式后再判断函数的图象，也可以采用“以静观动”，即将动点置于某些特殊的位置考察图象的变化特征，从而作出选择.

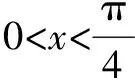
2.知图求式

例5(2015年新课标Ⅰ)函数f(x)=cos(ωx+φ)的部分图象如图所示，则f(x)的单调递减区间为( ).

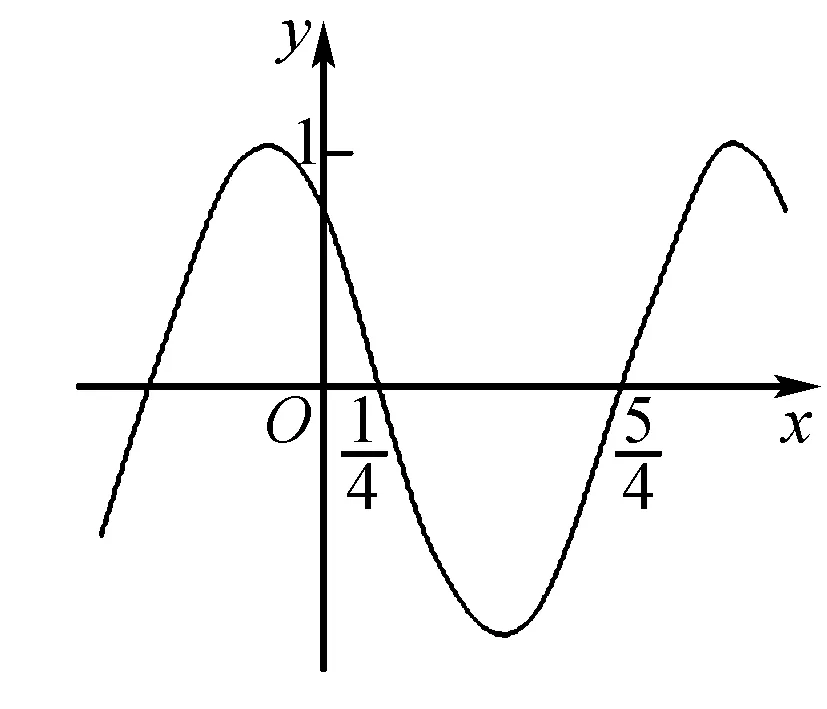
分析由图可求函数f(x)的解析式，进而求出函数的单调递减区间.

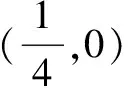
巧思由图可求函数f(x)的周期和初相，再求单调递减区间，进而得出结论.

点评本题主要考查函数y=Acos(ωx+φ)的图象和性质，数形结合是解题的关键.

三、函数图象的应用

函数图象的应用也是高考的热点.函数图象形象地显示了函数的性质，为研究数量关系问题提供了“形”的直观性，它是探求解题途径，获得问题结果的重要工具.以函数图象为工具来解决数学问题，体现了数形结合的数学思想.应用函数图象研究函数的性质，解方程或不等式，解决零点问题、恒成立问题、存在性问题都是常见的题型.

1.研究函数的性质

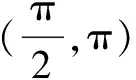
A．①②④ B．②④ C．①④ D．①③

分析易知f(x)是偶函数.根据绝对值的性质化简解析式，作出函数的图象即可作出判断．

解答∵f(-x)=sin|-x|+|sin(-x)|=sin|x|+|sinx|=f(x)，∴函数f(x)是偶函数.

由图可得①、④正确，故选C．

点评本题主要考查与三角函数有关的命题真假的判断，正确画出函数的图象是解决本题的关键．

2.解方程或不等式

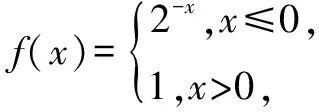
A．(-∞，-1] B．(0,+∞)

C．(-1,0) D．(-∞,0)

分析画出函数y=f(x)的图象，利用函数的单调性列出不等式求解即可．

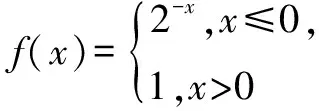
点评本题考查分段函数的应用，考查函数的单调性以及不等式的解法，考查计算能力．

3.零点问题

A．[-1，0) B．[0，+∞)

C．[-1，+∞) D．[1，+∞)

分析由g(x)=0得f(x)=-x-a，分别作出函数y=f(x)和y=-x-a的图象，根据图象交点的个数即可求出a的取值范围．

解答由g(x)=0得f(x)=-x-a，作出函数y=f(x)和y=-x-a的图象如图.

当直线y=-x-a的截距-a≤1，即a≥-1时，两个函数的图象有2个交点，函数g(x)存在2个零点.

所以实数a的取值范围是[-1，+∞)，故选C．

点评本题主要考查分段函数的应用，把函数g(x)的零点问题转化为函数y=f(x)和y=-x-a图象的交点问题是解决本题的关键．

4.恒成立问题

分析这是一个恒成立的问题，借助函数y=4x和y=logax的图象和性质可解.

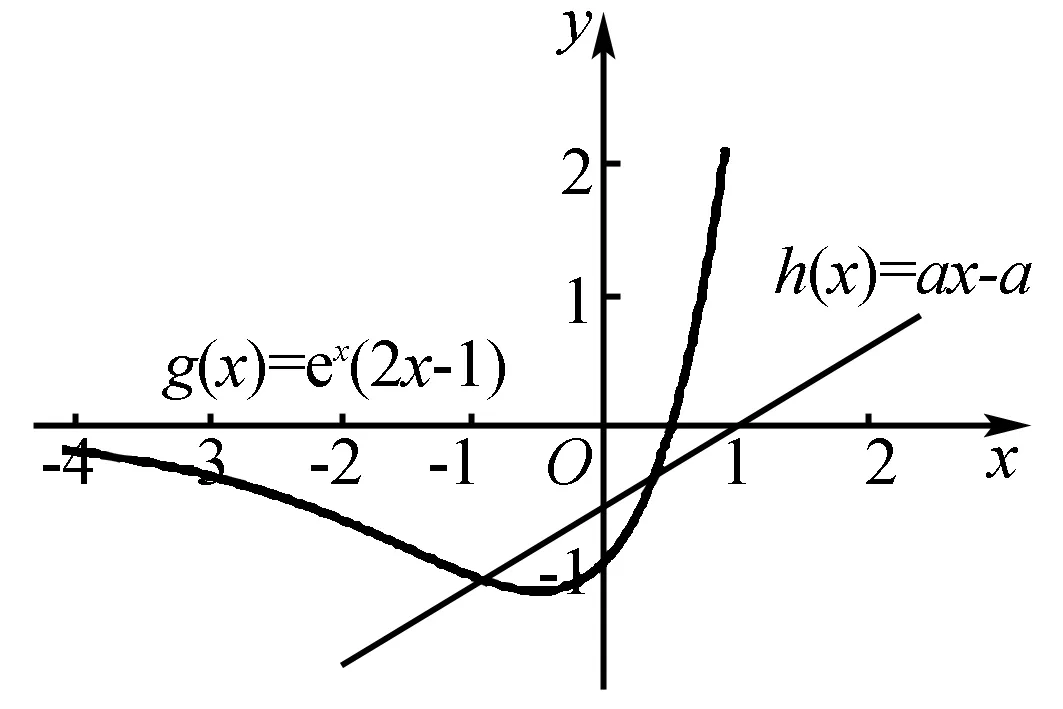
解答当a>1时，logax<0，显然4x

点评本题主要考查指数函数和对数函数的图象和性质，不等式恒成立问题的一般解法，属基础题.

5.存在性问题

例10(2015年新课标Ⅰ)设函数f(x)=ex(2x-1)-ax+a，其中a<1，若存在唯一的整数x0使得f(x0)<0，则a的取值范围是( ).

分析设g(x)=ex(2x-1)，h(x)=ax-a，问题转化为存在唯一整数x0使得g(x0)

解答设g(x)=ex(2x-1)，h(x)=ax-a.

点评本题考查函数的导数和极值，涉及数形结合和转化的思想，属中档题．

总之，绘制函数图象要规范、准确；识辨函数图象要善于读图；应用函数图象解题要灵活构造函数，并作出图象. 熟练掌握基本初等函数的图象和性质，是解决这类问题的前提.