高中数学中导数解题教学策略

潘万超

(福建省福州第十一中学 350001)

一、利用导数求解曲线切线问题

用导数求曲线的切线方程，是高考重点考查的知识点之一.以下针对导数法求切线方程的常见题型进行归类分析，并提出几点有效的教学策略.

1.已知切点求切线方程

策略一求导数→代切点→得斜率→切线方程

例1 曲线y=x3+11在点P(1,12)处的切线与y轴交点的纵坐标是____.

解析f′(x)=3x2，则在点P(1,12)处切线的斜率k=f′(1)=3，故所求切线方程为y-12=3(x-1)，化简得y=3x+9.令x=0，则y=9.

2.已知切线过某点求切线方程

策略二设切点→求导数→点斜式→代入已知点→切线方程

例2 已知曲线y=x3+11，求过点P(0,13)且与曲线相切的直线方程.

3.双切点未知求公切线方程

策略三设两个切点→求两个导数→点斜式方程组→斜截式方程组→由斜率相等、纵截距相等得参数值→切线方程

例3 (2016新课标全国Ⅱ卷 理16)若直线y=kx+b是曲线C1：y=lnx+2的切线，也是曲线C2：y=ln(x+1)的切线，则b=____.

点评在求曲线的切线方程时，注意两个“说法”，即“求曲线在点P处的切线方程”和“求曲线过点P的切线方程”，前者指明了以点P为切点，后者点P可能是切点，也可能是切线经过的某个已知点.学生解答此类问题有两个易错点：其一，审题不认真，未对点P的位置进行判断，误以为P一定是切点(比如例题2)；其二，当所给点不是切点时，无法利用导数的几何意义进行联系，不懂得预设切点坐标(比如例题3).因此，解决与导数的几何意义有关的问题时，要提醒学生首先确定已知点是否为曲线的切点是正确求解的关键所在.

二、利用导数求解导数单调性问题

单调性问题是高中数学的重要知识点，有效利用导数判断区间内函数的单调性，其本质就是判断导数的正负问题，在实际的解答中，证明不等式f′(x)≥0(或f′(x)≤0)在相应区间内恒成立，并且不恒为零.一般来说，首先需要明确函数的定义域，然后求出函数的导数，接着对导数的正负进行判断得出相应的结论.如果题目中没有明确x的范围，需要先求解出定义域，在定义域内完成单调性的讨论.

例4 设函数f(x)=emx+x2-mx.证明：函数f(x)在(-∞，0)上单调递减，在(0，+∞)上单调递增.

此题主要考查学生对导数概念、导数几何意义的理解，根据函数的相关性质完成解题.面对含字母系数的函数单调性问题，策略之一是利用分类讨论思想解题，需要根据函数求解导数，并且对其区间内的正负进行判断.策略之二是对原函数f(x)进行二阶求导，会收到意想不到的效果，避免了分类讨论.

策略一利用分类讨论思想

解析根据已知中函数f(x)得出f′(x)=m·emx+2x-m=m(emx-1)+2x.当m≥0时，x∈(-∞，0)时，emx-1≤0，f′(x)<0；当x∈(0，+∞)时，emx-1≥0，f′(x)>0；当m<0时，x∈(-∞，0)时，emx-1>0，f′(x)<0；当x∈(0，+∞)时，emx-1<0，f′(x)>0.因此，当x∈(-∞，0)时，函数f(x)单调递减；当x∈(0，+∞)时，函数f(x)单调递增.

策略二利用f(x)的二阶导数

解f′(x)=m·emx+2x-m，注意到f′(0)=0，于是再求导得到f″(x)=m2emx+2.由于f″(x)>0，于是y=f′(x)为单调递增函数，又f′(0)=0，所以当x∈(-∞，0)时，f′(x)<0；当x∈(0，+∞)时，f′(x)>0.即当x∈(-∞，0)时，函数f(x)单调递减;当x∈(0，+∞)时，函数f(x)单调递增.

点评利用导数判断函数的单调性判断时，如果函数解析式中含有参数，且参数对导数的正负判断有影响，需要对参数进行相应的分类讨论，进一步判断导数的正负，这是通性通法.当然，如果能观察出一阶导数的零点根，可以借助二阶导数判断一阶导数的符号，进而判断原函数的单调性，也是重要的方法补充.

三、利用导数求解函数图象问题

函数图象是高考考查的重点内容，对学生推理能力和数形结合思想有着比较高的要求.需要学生明确导数和函数图象之间的联系，如导数正负对函数单调性的影响，导数绝对值大小对图象走势影响等.同时需要从导数图象中提出相关的信息，导数正负值对应着函数单调性，图象和x轴交点等.

例5 如图中所示，一个正五角星的薄片，对称轴和水面垂直，匀速从水面露出，假如五角星露出水面的时间为t，露出水面的面积是S(t)(S(0)=0)，那么导函数y=S′(t)的图象大致为( ).

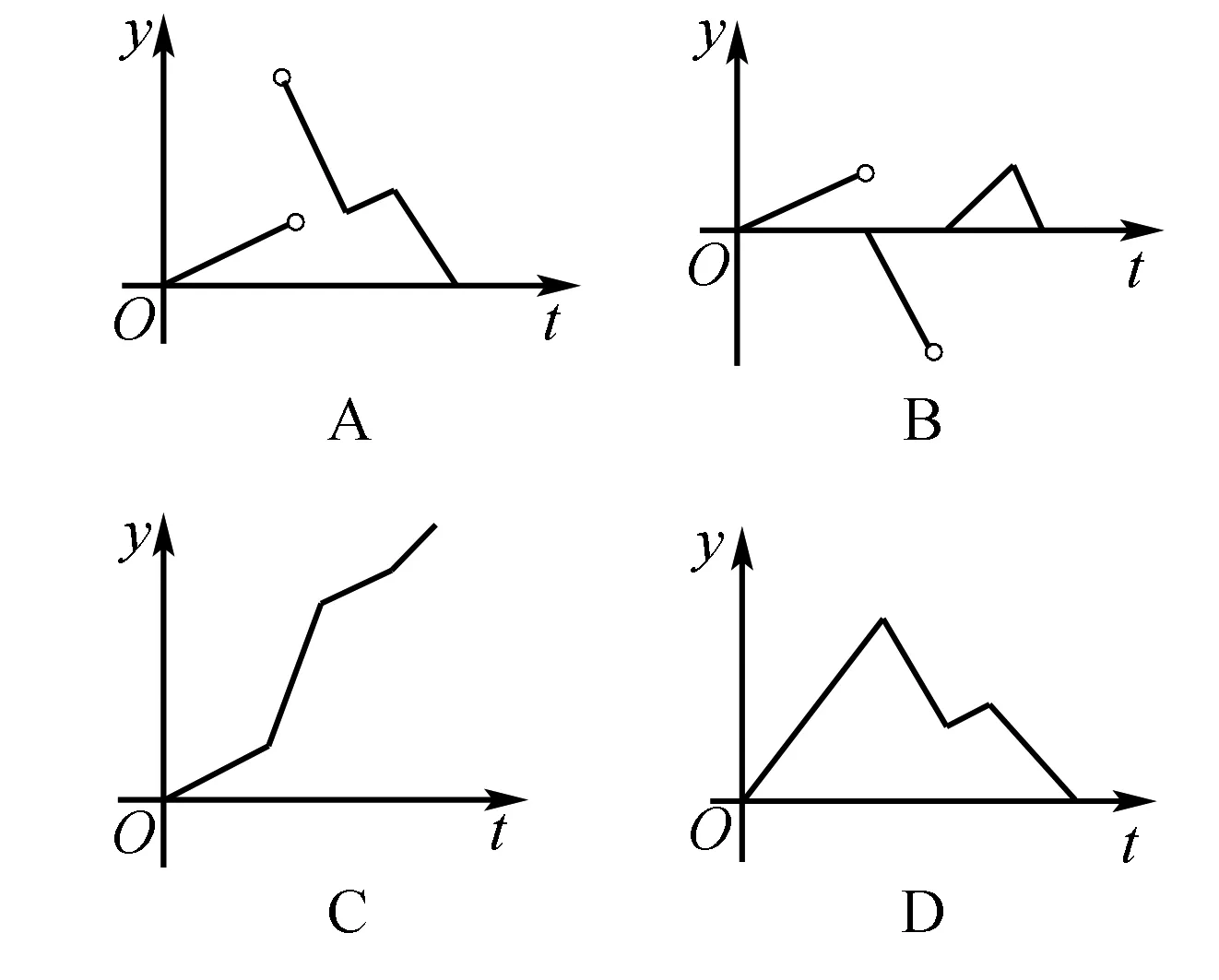
解析 策略一直接法

根据正五角星的形状，开始面积增加的幅度成直线状态，在某一时刻面积突然跳跃性地增大，此时S(t)的图象上反应为断点形状，是一个分段函数的图象，S′(t)也有类似变化，然后面积继续增加，但增加的幅度变小，接着面积增加的幅度又变大，然后变小.只有A符合，故选A.

策略二排除法

考察最初零时刻和最后终点时刻，面积没有变化，导数取零，排除C；总面积一直保持增加，没有减少，排除B；在正五角星两肩位置露出水面时，面积改变为突变，图象产生中断，故排除D.

点评本题考查函数图象、导数图象、导数的实际意义，重点考查学生对函数图象的识别能力，对导数的探究能力和应用能力.可以采用不同的教学策略帮助学生进行分析，比如可以将正五角星露出水面的过程分为四个阶段分别分析.也可以利用排除法，考察初始点和终结点是否吻合，某个特殊变化过程是否吻合，从而做出正确的选择.

导数是高中阶段的重要知识内容，在高考中有着非常大比重，导数具有工具性特点，并且和其他知识点有着密切的关系，使得导数问题非常的多样、复杂，面对导数问题常常无从下手.因此，结合相应的导数问题，对相关导数解题进行分析和探究，明确不同类型问题的解题思路，提高学生的解题能力，构建高效数学课堂.