“算两次”原理与“组合数”的完美邂逅

刘华荣

(江苏省泰州市溱潼中学,225508)

“算两次”看似很通俗,教学中它却可能被很多教师忽视甚至遗漏.学生在解题中偶有相遇,但大多不明其理,难究其因.其实“算两次”原理并不“神秘”,它在公式的推导、理解、记忆,新知识的产生以及解题方法的探索等方面的运用是十分广泛的,它体现了从两个方面解决问题的数学方法,更重要是蕴藏着从不同角度看问题的转换思想.当你面对难题苦思冥想,一筹莫展时,“算两次”总能出其不意,绝处逢生,给人以豁然开朗和屡建奇功之感.下面我们先认识一下何为“算两次”?

一、一见倾心——熟悉又陌生的“算两次”

什么是算两次?美国的数学家波利亚对“算两次”原理是十分推崇的,他形象地将其比喻为“抛两个锚安全系数更大”.波利亚说:“为了得到一个方程,我们必须把同一个量以两种不同的方法表示出来”,也就是将一个量从不同的角度、用不同的形式“算两次”,从而寻找相互的联系或建立相等的关系,这就是“算两次”原理,也叫“福比尼原理”.单墫教授在《算两次》一书中,也将算两次原理形象地比喻成“三步舞曲”.即从两个方面考虑一个适当的量,一方面…另一方面…综合起来…如果一个数学研究对象具有双重身份或两面性,说明既满足条件A,又满足条件B,就可以考虑这种方法.

例如，课本中的等差数列的前n项和公式是这样推导的:Sn=a1+a2+…+an=a1+(a1+d)+…+[a1+(n-1)d]，

①

将各项次序反过来,Sn又可以这样写:

Sn=an+an-1+…+a1=an+(an-d)+…+[an-(n-1)d].

②

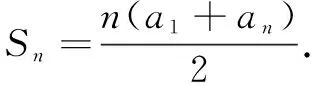
此处用倒序相加对Sn进行了两次不同形式的计算,使用了“算两次”的方法.

高中课本中“算两次”的运用比比皆是,再如两角和差余弦公式的推导,等面积和三棱锥中等体积方法的运用,平面向量数量积的计算公式,圆锥曲线的不同定义,以及下面我们要研究的组合数相关问题，等等.

二、小试牛刀——用“算两次”对组合数公式进行理解

很多组合数恒等式的证明,如果仅仅利用组合数的定义和阶乘运算来证明,枯燥无味,且很多学生会因陷入繁杂的计算而苦恼.我们可以用“算两次”的方法对课本中常用公式加以解释和理解.

(1)Cmn=Cm-nn理解为从n个学生中选取m个学生做班委，选法有Cmn种,从n个学生中选n-m个学生不做班委，选法有Cm-nn种,选上与剩下的一一对应,所以组合数相等.

(2)Cmn+Cm-1n=Cmn+1.可理解为某班包含学生甲共n+1人,现从n+1个学生中选取m个学生做班委有Cmn+1种,另从n+1个学生中选取m个学生做班委,m个班委中一定含甲的有Cm-1n种,一定没有甲的有Cmn种,总数为Cmn+Cm-1n，所以Cmn+Cm+1n=Cmn+1.

(3)kCkn=nCk-1n-1.可 理解为从n个学生中先选k个学生做班委,再从k个班委中选一人做班长有kCkn种.换一个角度思考,若先选班长有C1n种,再从n-1个学生中选k-1个学生做班委有Ck-1n-1种,所以有C1nCk-1n-1=nCk-1n-1.

(4)C0n+C1n+C2n+…+Cnn=2n.可考察{a1,a2,…,an}中子集的个数,先根据子集中含有元素的个数进行分类,子集中含有零个元素有C0n种,子集中含有一个元素的有C1n种,子集中含有两个元素的有C2n种,…子集中含有n个元素的有Cnn种， 子集总数为C0n+C1n+C2n+…+Cnn；从另一个角度理解,每一个元素成为子集的可能性都只有两种,共n个元素,所以共有子集2n个.

组合数的推广公式还有很多,它们多数可以用“算两次”的原理去理解,此处就不再一一列举了.教师在课堂上除了用严密的代数证明之外,若也能用“算两次”的方法去解释它们,可以激发学生的兴趣,帮助理解,方便记忆,也为我们的课堂增添了色彩.

三、实战演练——算两次原理在组合解题中的运用

例1求值:C12 020+2C22 020+3C32 020…+2 020C2 0202 020.

解析令T=0C02 020+C12 020+2C22 020+3C32 020…+2 020C2 0202 020.

①

将① 倒序相加，得T=2 020C2 0202 020+2 019C2 0192 020+…+2C22 020+C12 020+0C02 020.

②

①+②，得2T=2 020(C02 020+C12 020+C22 020…+C2 0202 020)=2 020·22 020，

即T=2 020·22 019.本题也可以借助kCkn=nCk-1n-1公式化简或构造(1+x)2 020的展开式求导赋值也较为简单,此处就不再赘述了.

变式1求值:C02 020+22C22 020+24C42 020+26C62 020…+22 020C2 0202 020.

解析根据给出式子的结构,尝试构造两次二项式定理如下:

(1+2)2 020=C02 020+21C12 020+22C22 020+23C32 020…+22 020C2 0202 020.

①

(1-2)2 020=C02 020-21C12 020+22C22 020-23C32 020…+22 020C2 0202020.

②

变式2已知(1+x)2 020=a0+a1x+a2x2+a3x3+…+a2 020x2 020,求a0+a2+a4··+a2 020.

解析采用两次赋值法.先令x=1:22 020=a0+a1+a2+a3+…+a2 020；

①

再令x=-1:0=a0-a1+a2-a3+…+a2 020.

②

解析可考虑将其用二项式定理打开:

①

②

例2证明:(C0n)2+(C1n)2+(C2n)2+…+(Cnn)2=Cn2n(n∈N*).

解析二项式系数相乘的问题可以尝试两个二项式定理相乘,运用算两次的原理,确定其为某指定一项的系数,建立等价关系.考虑:

(1+x)n(1+x)n=(C0n+C1nx+C2nx2+…+Cnnxn)(C0n+C1nx+C2nx2+…+Cnnxn).

左边(1+x)n(1+x)n=(1+x)2n含xn的系数是:Cn2n；

右边含xn的系数是:C0nCnn+C1nCn-1n+C2nCn-2n…+CnnC0n=(C0n)2+(C1n)2+(C2n)2+…+(Cnn)2.

所以(C0n)2+(C1n)2+(C2n)2+…+(Cnn)2=Cn2n.

变式1证明:C0nC1n+2C1nC2n+3C2nC3n+…rxCr-1nCrn+…+nCn-1nCnn=nCn-12n-1(n∈N*).

解析本题也可借助于算两次原理,但在形式上增加了难度,考虑到二项式系数前面含有其他的系数,可寻找公式将其处理.

法一由kCkn=nCk-1n-1，得

左边=nC0nC0n-1+nC1nC1n-1+nC2nC2n-1+…+nCn-1nCn-1n-1

=n(C0nC0n-1+C1nC1n-1+C2nC2n-1+…+

Cn-1nCn-1n-1).

考虑:(1+x)n(1+x)n-1=(C0n+C1nx+C2nx2+…+Cnnxn)(C0n+C1nx+C2nx2+…+Cn-1n-1xn-1).

继续借助算两次原理,求得(1+x)n(1+x)n-1=(1+x)2n-1含xn-1的系数为Cn-12n-1.

而(C0n+C1nx+C2nx2+…+Cnnxn)(C0n-1+C1n-1x+C2n-1x2+…+Cn-1n-1xn-1)含xn-1的系数为:

=C0nCn-1n-1+C1nCn-2n-1+C2nCn-3n-1+…+Cn-1nC0n-1=C0nC0n-1+C1nC1n-1+C2nC2n-1+…+Cn-1nCn-1n-1.

所以C0nC0n-1+C1nC1n-1+C2nC2n-1+…+Cn-1nCn-1n-1=Cn-12n-1.

证得C0nC1n+2C1nC2n+3C2nC3n+…xCr-1nCrn+…+nCn-1nCnn=nCn-12n-1(n∈N*).

法二利用导数,由二项式定理,(1+x)n=C0n+C1nx+C2nx2+C3nx3+…+Cnnxn，

①

两边求导,得n(1+x)n-1=C1n+2C2nx+3C3nx2+…+nCnnxn-1.

②

①×②，得n(1+x)2n-1=(C0n+C1nx+C2nx2+…+Cnnxn)(C1n+2C2nx+3C3nx2+…+nCnnxn-1)

继续运用算两次原理,寻找含xn-1的系数,就与上题相似了.

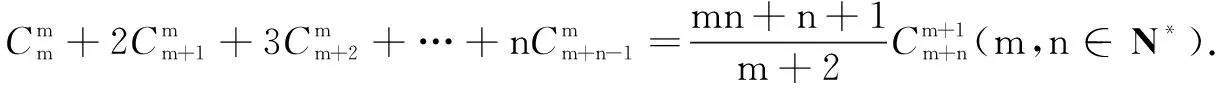
解析观察发现本题较上一题组合数的下标是m,m+1,m+2,m+n-1是变化的,构造类似的代数式就于事无补了,于是尝试构造:

f(x)=(1+x)m+2(1+x)m+1+3(1+x)m+2+…+n(1+x)m+n-1(x≠0,x≠1).

此式各项展开式中含xm项的系数为Cmm+2Cmm+1+3Cmm+2+…+nCmm+n-1.继续从另一个角度研究函数f(x),通过化简继续寻找含xm项的系数,发现其可以借助错位相减法进行合并.

f(x)=(1+x)m+2(1+x)m+1+3(1+x)m+2+…+n(1+x)m+n-1①,左右两边同乘1+x，得

(1+x)f(x)=(1+x)m+1+2(1+x)m+2+3(1+x)m+3+…+n(1+x)m+n.

②

①-②，得-xf(x)=(1+x)m+(1+x)m+1+(1+x)m+2+…+(1+x)m+n-1-(1+x)m+n

求得f(x)=

f(x)中含有xm项的系数，即为其分子中含xm+2的系数,即nCm+1m+n-Cm+2m+n,继续化简.

而nCm+1m+n-Cm+2m+n

得证.

笔者通过对“算两次”原理粗略地研究发现,课本中很多的定义、公式、表示法的多样性体现了“算两次”思维的灵活性.教学中我们不可一味地灌输知识,苦战题海.教者应该不断挖掘教材潜能,不仅要触类,更要精通.要努力于引导学生主动分析问题的背景结构,尝试解决的途径,提炼解决问题的新原理、新方法,才能更多地拓展新知识,探索新领域.