数学学科分层走班下B层教学实施策略
刘沁桥 晏伟

学生之间存在着个体差异。笔者结合“伴生课堂”教学模式的“定向开启、示疑互动、悟理明法、入脑融合”四个环节,重点谈谈数学学科分层走班下B层教学实践策略。
一、拟定目标,启发思维
问题是课堂教学的开端,只有学生感到需要问“为什么”“是什么”“怎么办”的时候,思维才会真正启动。
教学人教版七年级数学上册《球赛积分问题》时,A层可以设计选择题:某球队参加比赛,开局9场保持不败,积21分,比赛规则胜一场得3分,平一场得1分,则该队共胜( )场。
A. 4场 B. 5场 C. 6场 D. 7场
教师出示题目之后提问:题目中有哪些已知量,那些未知量?怎样用式子表示总积分与胜、负场数之间的关系?
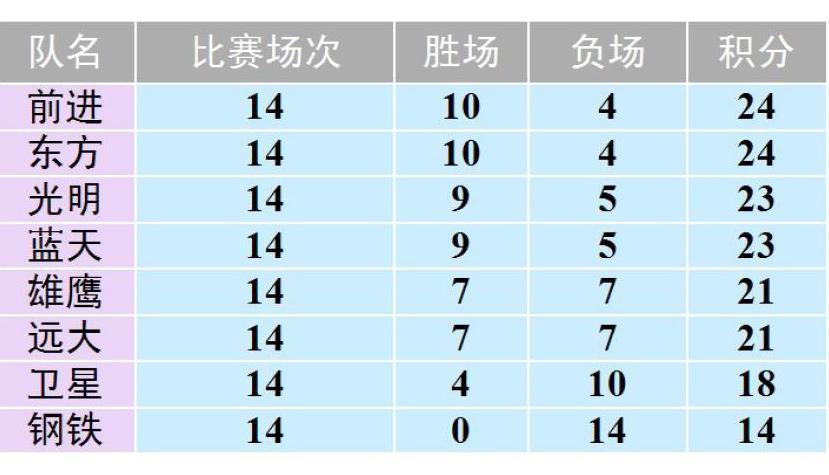
对于B层学生,则直接展示下面表格:某次篮球联赛积分榜如下:
然后,教师再出示以下问题,①你能从表格中看出负一场积多少分吗?②你能进一步算出胜一场积多少分吗?③怎样用式子表示总积分与胜、负场数之间的关系?④某队胜场总积分能等于它负场总积分吗?
问题①要求学生能迅速找出特殊行或特殊列,将总积分与胜负场数对应起来,问题④是在前面问题解决之后的灵活应用。而A层的两个问题提出后,学生基本能够根据题目推导出等量关系,难度较B层有所降低。
二、疑而思变,互动共生
教师应通过拓展问题,让学生在互动中弄清问题的本质。
人教版七年级数学上册3《销售中的盈亏问题》中有这样一道例题:商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25%,另一件亏损25%,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
A层学生拓展问题是这样设计的:①若以同样价格卖出这两件衣服,其中一件盈利35%,另一臺亏损35%。这次商店是盈利还是亏损,或是不盈不亏?②若以同样价格卖出这两件衣服,其中一件盈利15%,另一台亏损15%。这次商店是盈利还是亏损,或是不盈不亏?
B层学生的拓展问题是这样设计:①若以同样价格卖出这两件衣服,其中一件盈利35%,另一台亏损15%。这次商店是盈利还是亏损,或是不盈不亏?②其中一件盈利15%,另一件亏损35%。这次商店是盈利还是亏损,或是不盈不亏?
A层学生的两个拓展问题是在原题的基础上进行数值的修改,但不管是盈利还是亏损的百分比数值都是一样的,其中一个数值比25%高,一个数值比25%低。这样重复地取值,就是为了引导学生能够推测出最后不管盈利和亏损的百分数是多少,只要百分比是一样的,就一定是亏损的规律。而B层学生的两个拓展问题则是在同样前提下,给出的商品盈利和亏损的百分数不一样,并且其中一个是在原题25%的基础上增加10%的盈利,减少10%的亏损,一个是在原题25%的基础上,减少10%的盈利,增加10%的亏损。这样的设计就要求学生在掌握A层问题得出的规律后,还能够进行举一反三。
三、详略有别,细悟不同
不同的引导方式,都应回归题目本质,从“整体”中分离出“部分”,进而求解。
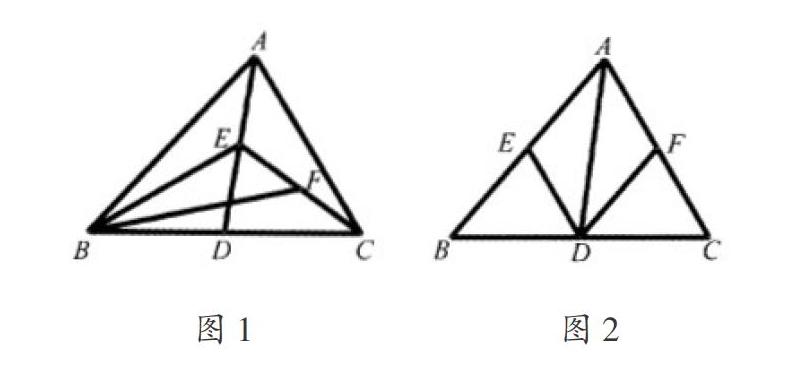
教学人教版八年级数学上册《三角形的中线》时,教师对A层学生设计的题目是这样的:(1)如图1,已知△ABC,点D,E,F分别是BC,AB,AC的中点,若△ABC的面积为16,则△ABD的面积是 ,△EBD的面积是 。(2)如图2,点D,E,F分别是BC,AD,EC的中点,若△ABC的面积为16,求△BEF的面积是多少?
对B层学生直接设问:如图,已知点D,E,F分别是BC,AD,EC的中点,若△ABC的面积为16,求△BEF的面积是多少?
这道题属于中等偏上难度,对A、B两个层次的学生要求不同,但不管是A层还是B层的题目都要进行相同的引导,那就是首先要求S△ABD,S△EBD,S△ADF与S△ABC的关系。
对A层的学生从画图中开始引导(如下图):
教师提出如下问题,①S△ABD与S△ABC面积有怎样的联系?②取AD中点E,如何比较S△BED与S△CED的大小,并说明它们与S△ABC有怎样的关系?(说明中线等分面积的实质)③在图4中,进一步,取EC中点F,连接BF,探求S△EBD与S△ABC的关系(通过图形分离,层层推进,训练他们几何的逻辑思维)。
对B层学生从三角形的面积公式入手,学生容易得出三角形的面积大小是通过底和高这两个量决定的,进而推出S△EBD=S△EDC=[14]S△ABC,得出中线等分面积的结论。
四、入脑融合,无惧变化
对上述题目而言对A层学生应让他们继续对图形进行探究,并小组合作,探讨还能求出图中哪些三角形的面积,逐一列举,深化学生对中线等分面积这一数学思想的理解和应用。
对B层学生则设置一道全新的题目:如图5,△ABC 中,D,E,F分别是CE,AF与BD的中点,已知△DEF的面积为1,求△ABC的面积。
此题难点在于,由题中三个中点,在△ABC中无法找到相应的中线,无从寻求△DEF与△ABC的面积关系。如何让D,E,F转化为相对应的中线是关键,连接AD,BE,CF使其转化成三角形的中线,添加辅助线构造3个三角形(图6)。从复杂图形中分离出简单模型,学生理解更为流畅自然。
(作者单位:武汉经济技术开发区第一初级中学官士墩校区)
责任编辑 张敏
——书写要点(三)

