基于磨耗定量的地铁曲线钢轨波磨发展机理研究

郑灵霞， 尧辉明

(1 上海工程技术大学 城市轨道交通学院， 上海 201620； 2 同济大学 铁道与城市轨道交通研究院， 上海 201804)

0 引 言

从二十世纪六十年代开始，中国铁路上逐渐出现一种波浪形的磨耗，简称波磨。波磨不仅在钢轨上产生剧烈的磨耗，而且会对铁路周边的环境造成噪声污染，对车辆轨道零部件的寿命、乘坐舒适度以及行车安全性都会有一定影响。所以，研究波磨的形成及其发展是有必要的。

由于运行线路状态以及车辆参数的不同,各国学者们所提出的波磨形成机理也不尽相同，关于波磨成因始终没有一个成熟统一的说法。近年来，由于地铁客流量变化大、线路小半径曲线较多，加之站间距短导致的车辆启动与制动频繁，波磨在地铁上也屡见不鲜。一些小半径曲线线路从缓和曲线至圆曲线，甚至出现了逐渐增加的严重波磨。所以本文针对小半径曲线上的波磨形成之后的发展机理进行研究，并基于波磨的形成机理为轮轨之间的蠕滑导致的粘滑振动的假设，建立一个钢轨型面磨耗量的计算模型，模型考虑轮轨动力学、轮轨接触分析以及材料磨损计算三个部分，以进行对波磨发展机理的磨耗定量验证。

1 波磨形成与发展机理

钢轨波磨作为世界性难题，近百年来，各国的学者们对波磨的成因、危害和防治措施进行了不少研究，仍没有获得彻底消除波磨的解决办法。Grassie等人[1]将波磨形成机理概括成2个特征：固定波长机理和磨损机理，并总结了波磨的形成机理，如图1所示。Hempelmann等人[2-3]认为轮轨结构反共振的高接触力为钢轨波磨的成因。Suda等人[4-5]对塑流型波磨进行了研究，研究认为轮轨自激振动为波磨的形成机理。范钦海[6-7]则基于轮轨之间的粘滑振动提出波磨的波磨成因理论，对轮轨间的磨耗功进行了模拟研究。

图1 波磨形成机理

上述学者们所阐述的波磨成因虽然不尽相同，但其中大多都认同Grassie等人[1]的分类方法，即波磨的形成是轮轨动力学和接触力学的循环反馈过程，且同时伴随钢轨的长期磨损。从轮轨的接触斑上窥探的轮轨动力学和接触力学则如图2所示，接触斑纵向上的法向压力会导致轮轨之间的塑性变形，而切向力会导致轮轨之间的蠕滑，并将接触斑划分为粘着区和滑动区。当轨道车辆通过小曲率半径轨道或由于加速和制动过程产生较大的纵向力情况下,接触斑内的滑动区域逐步扩大, 最后整个接触斑全为滑动区。在轮轨状态变为全滑动时，轮轨间轻微的颤动将会导致粘滑振动的发生。

图2 轮轨接触斑范围内的受力情况

Matsumoto等人[8]的论文中详细描述了粘滑振动的发生过程。轮轨之间的接触部分在轮轨间没有振荡的情况下，蠕滑力和蠕滑率之间的关系如图3(a)所示，在蠕滑率—蠕滑力关系曲线上存在一个负斜率段，在负斜率段，微弱的激扰将会使车轮载荷发生振荡。图3(b)则为轮载振荡时，蠕滑力在FH和FL之间的变化，曲线②表示是的负载最大值时蠕滑力特性，曲线③是负载最小值时蠕滑力特性。车轮负载振动时，在车轮负载降低过程中，车轮开始产生滑动，通过曲线上的B点，然后通过惯性达到蠕滑率最大值点C，当车轮负载回复到平均值时，车轮与钢轨又开始处于粘着情况，蠕滑率开始突然降低，达到车轮负载最大值点D，因此轮轨间产生了A-B-C-D的这样一个循环，即轮轨间接触斑在粘着区和滑动区的交替过程。

(a) 无振荡时 (b) 振荡时

因为轮轨之间的磨损仅在接触斑在滑动区时发生，则根据粘滑振动的发生过程，推测初始波磨形成时，车轮载荷振荡导致轮轨蠕滑力振荡，致使轮轨间出现粘滑振动，且蠕滑力振荡幅度大处成为波磨的波谷，振荡较小处位于波磨的波峰[9]。波磨形成之后，受惯性影响，波峰处的垂向压力大于波谷处的垂向压力，波峰处使得粘着状态失效的蠕滑力就要大一点，所以高点处粘滑振动的幅度相较于低点处小。从磨耗量的角度来看，这个现象表现为波磨高点处的磨耗量要比低谷处的磨耗量小，如图4所示，这也是波磨逐渐加深发展的原因。本文将以曲线线路上的粘滑振动为中心，建立一个仿真模型对钢轨波浪形磨耗从磨耗量的角度进行定量研究。

图4 波磨发展机理

2 建立钢轨波浪形磨耗量的仿真计算模型

2.1 仿真思路

钢轨波浪形磨耗计算模型的建立考虑4个模块，包括轮轨耦合动力学仿真、轮轨滚动接触分析、材料磨损计算集成的钢轨磨耗量计算过程，以及磨耗后钢轨波磨型面的更新过程，具体如图5所示。

仿真的主要思路为：线路及车辆参数输入后，经过动力学计算，得到动态的轮轨动力学参数；通过轮轨接触几何分析可以得到接触斑的形状，轮轨接触力学获得接触斑表面接触力密度及滑动量的分布，通过一定方式叠加即可得到沿车辆行驶方向的波磨深度；由于动力学计算比较耗时，研究则进行多次磨耗计算后再进行动力学计算，设置当车辆运行达到一定次数时对钢轨型面更新，对型面的更新结果再进行新的动力学和磨耗计算，如此反复。

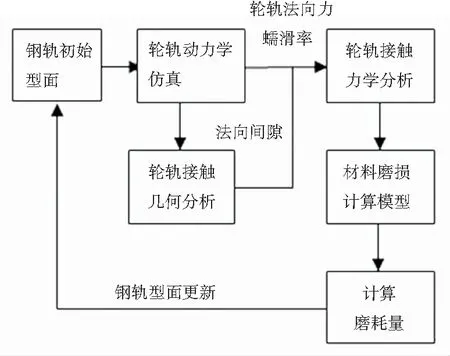
图5 钢轨磨耗计算流程

本文主要以曲线上的粘滑振动为出发点研究，而在实际仿真中发现，车辆的一系定位刚度对粘滑振动基本无影响，整车仿真的计算也表明，二系悬挂刚度对波磨也无影响[10]，并且多名学者[11-13]的研究发现簧下质量对波磨的形成具有很大的影响，所以选用单轮对模型代替整车模型来进行钢轨波浪形磨耗的研究，并应用hertz非弹性接触理论来耦合轮轨之间的垂向关系，即因轨道不平顺引起的垂向作用力为：

(1)

其中，G为轮轨接触常数，δZ(t)为轮轨间的弹性压缩量。

在轮轨接触模型中，kalker精确理论由于计算耗时太长，一般不会用于时域仿真计算，而Vermeulen-Johnson理论在粘着区和滑动区的划分方面略有不足，故采用kalker的简化理论来计算轮轨接触过程中的参数。kalker的简化理论中接触斑上纵、横向蠕滑力及垂向力矩可以表示为：

(2)

其中，ξx，ξy，φ分别为接触斑纵向、横向、自旋蠕滑率；a，b为接触斑的长短轴；Cij为蠕滑系数。

目前，主要用于计算车轮和钢轨之间磨耗的计算模型有2种。一种是考虑能量耗散的角度，建立相应的磨耗功模型；另一种是材料磨损模型，其中比较典型的有Archard模型、Jendel模型和braghin模型。这些模型都是以实验和经验为基础并在实际中得到较好运用的。而Archard磨损模型计算所需的参数较其他模型更容易取得，计算结果也更符合实际，故利用较为经典的Archard模型建立钢轨波磨计算模型。

2.2 Archard磨损模型在计算钢轨波浪形磨耗时的应用

Archard磨损模型的一般公式如下：

(3)

其中，V为钢轨的磨损体积；P为轮轨接触法向压力；S为轮轨的相对滑动距离；H为材料硬度；K为磨耗系数。

为了使接触斑上的磨耗量的计算更精确，应对接触斑进行网格划分。在处理时，采用kalker简化理论以及Hains和ollerton条形理论的计算策略。在kalker简化理论中，将轮轨接触参数进行无量纲化处理，则接触斑可转换为如图6所示的单位圆进行离散。为了研究粘滑振动对钢轨波磨的形成的影响，需要对钢轨纵向磨耗量的分布做清晰明了的表达，所以与条形理论的处理不同的是，平行于钢轨型面划分长方形带，将每个矩形条再按照步长离散成单元格。则接触斑上每个单元用Archard材料磨损理论计算的磨耗体积损失ΔVw(x,y)为：

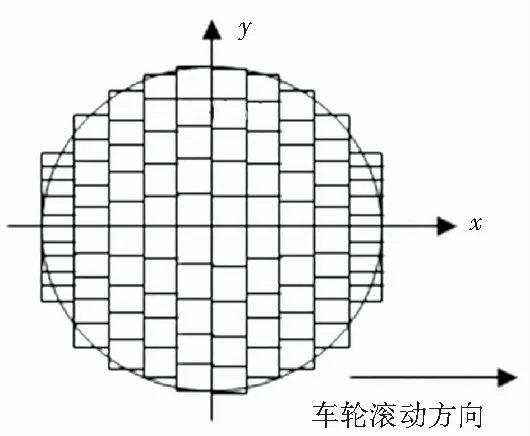
图6 接触斑网格划分

(4)

其中，kw(x,y)为每个离散单元上的磨耗系数。磨耗系数k的取值变化范围与单元上滑动速度与正压力的关系如图7所示。图7中的磨耗系数是在干燥清洁的条件下试验得到的。但在实际计算时很难针对特定的滑动速度和正压力确定特定的磨耗系数，出于对简便计算的考虑，不同区域里的磨耗系数取中间值代替，即k1=3.5×10-2,k2=5×10-4,k3=3.5×10-3,k4=5×10-4。

图7 磨耗系数

对于轮轨相对滑动距离Δs(x,y)，在接触斑的粘着区内，轮轨之间不存在相对滑动，所以滑动距离为零；只有位于滑动区时，才有磨耗发生，此时滑动距离的计算公式可表示为：

(5)

其中，v(x,y)为每个单元格中心轮轨的相对滑动速度；vt为车辆行驶速度；dx为行驶方向上一个计算单元内的运动长度；v(x,y)可以由下式计算：

(6)

其中，ux(x,y)，uy(x,y)则分别为质点在纵向和横向的弹性位移，在计算时，弹性变形产生的速度分量极小，因此计算中经常将其忽略。

通过以上计算可以得到接触斑内每个离散单元上的磨耗体积损失ΔVw(x,y)，进而可以得到每个离散单元对应的磨耗深度Δhw(x,y)，此时需用到如下数学公式：

(7)

单个接触斑上每个单元格上的磨耗量需要叠加到一起。为了简化计算，对轮轨接触状态提出一个假设：车轮滚过一个接触斑时，车轮与钢轨的接触状态不变，包括行驶速度、正压力、滑动速度、接触斑面积等。由于选择的线路较简单，所以让车轮重复通过一段曲线线路，以车辆通过的行程或通过这一段路程的次数作为钢轨型面更新的依据。

3 计算结果与分析

3.1 计算条件

仿真计算中，设置单轮对在半径为200 m的曲线轨道上运行，车辆参数使用地铁A型车的结构参数，见表1。轨道参数取进出缓和曲线为20 m，圆曲线长为50 m，设置轨底坡为1：40，轮轨型面分别为LM车轮磨耗型踏面和60 kg钢轨型面，车速为40 km/h，可以得到轮对在曲线上运行时，沿车轮滚动方向的磨耗深度分布。

表1 车辆参数

3.2 结果分析

图8表示的是轮对在地铁小半径曲线轨道上运行一次所形成的初始波磨。左轨初始波磨波峰峰值为0.55×10-4mm，最大磨损深度为1.33×10-4mm，从初始波磨的波峰到波谷的深度约为0.78×10-4mm。右轨初始波磨波峰峰值为0.67×10-4mm，最大磨损深度为1.9×10-4mm，波深约为1.23×10-4mm。钢轨的磨损从缓和曲线开始一直增加，至缓和曲线后段及圆曲线段形成波浪形的磨耗，到另一段缓和曲线处钢轨磨损的周期振动逐渐平缓，直至磨损消失。轮对在经过小半径曲线时，在缓和曲线处，蠕滑力在图3蠕滑区，轮轨间接触斑的滑动区增大，且磨耗仅在滑动区发生，所以钢轨的磨耗逐渐增加但并没有形成波磨。当蠕滑力达到图3所示的蠕滑力最高点时，接触斑粘着区消失，轮轨间的粘着状态将会失效。与此同时，由于粘着状态的失效，轮轴将释放由于左右车轮切向蠕滑力的不同所积聚的扭转能量。当扭转能量下降到轮对可接受能量范围之内时，轮轨粘着区出现，轮对又将积聚能量，粘着区增大、滑动区减小，导致磨耗量减小。即当轮对积聚能量时，磨耗量减小，能量达到饱和时，磨耗量增大。如此反复，形成周期性波动，初始波磨形成。

(a)外轨

(b)内轨

为了验证波磨形成之后，高点的磨耗程度较低点的磨耗程度小。在仿真中，于初始波磨的基础上加之周期0.2，波深为0.1mm的波磨，仿真结果如图9所示。从图9中可见磨耗量在波磨高点处周期颤振的幅度要比在低点处的小，即可以发展出，波长固定而由于波磨波峰与波谷的磨损差异导致波深不断加深的波浪形磨耗型面。

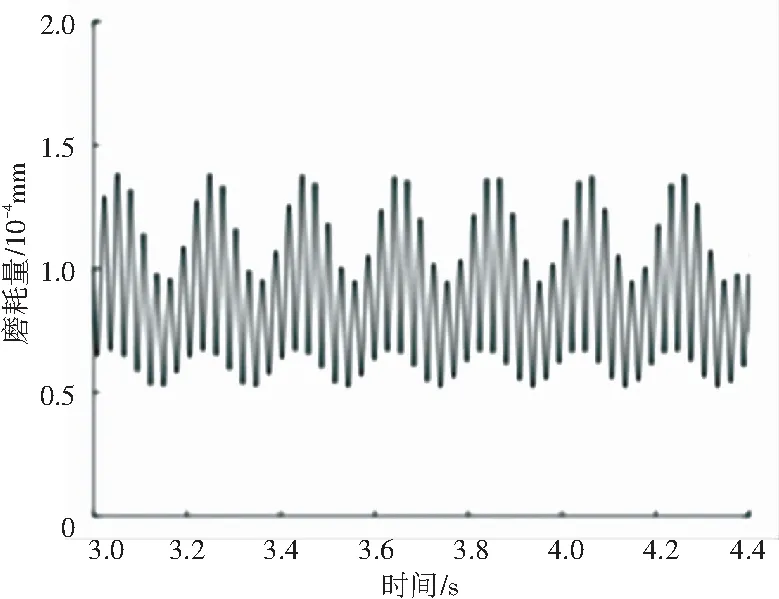
(a)外轨

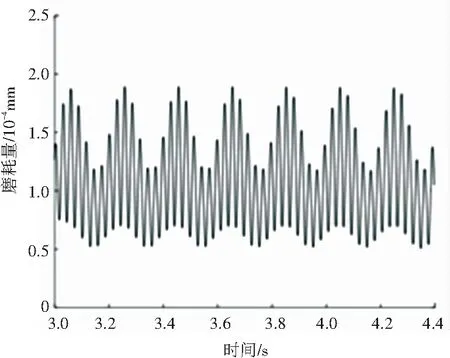
(b)内轨

图9 添加周期为0.2，波深为0.1 mm的波磨时，行驶一次所得的磨耗量

Fig. 9 When the addition period is 0.2 and the wave depth is 0.1 mm, the abrasion amount obtained during driving once

将波磨按照行驶距离即通过曲线次数叠加，可以清楚地得到波磨的发展过程。研究后得到的5条曲线见图10，即为轮对在圆曲线处的磨耗量，自下而上分别为轮对行驶1次、50次、100次、150次及200次的磨损量变化。行驶200次后，左轨波深为0.012 mm，右轨为0.019 mm，均约为初始波磨的154倍左右，左右轨磨耗速率大致相同。从图10中可以明显看出波磨波长无明显变化，形成初始波磨后，波峰处磨耗量与波谷处磨耗量的磨损差异不断拉大，致使波磨最大磨损深度不断增大，从而使得波磨不断加深发展。

(a) 外轨

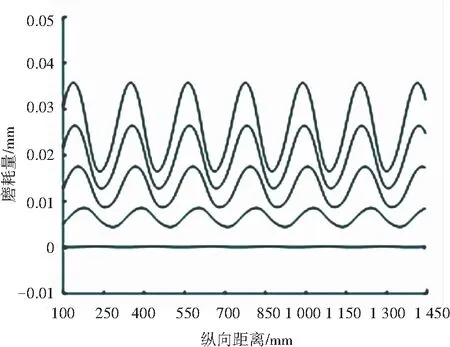
(b) 内轨

4 结束语

针对地铁小半径曲线段钢轨的磨耗情况，从磨耗定量的角度研究了波磨的形成与发展机理。利用Matlab/Simulink建立了一个集轮轨耦合动力学，轮轨接触分析以及材料磨损模型为一体的钢轨磨耗计算模型，其仿真结果和理论分析具有一致性。基于计算结果可以得出以下结论：

(1)地铁小半径曲线上的初始波磨由轮轨之间的粘滑振动，钢轨磨耗从缓和曲线段至圆曲线段呈上升趋势，在蠕滑力饱和之后的负斜率段内，钢轨磨耗周期振荡形成初始波磨。

(2)在波磨发展阶段，初始波磨的形成使得轮轨垂向力波动，导致波磨高点处的磨耗量要比低点处的小，形成波磨波峰波谷的磨耗差异，致使波磨不断加深，而波磨波长无明显变化。