基于奇异值分解的无参考立体图像质量评价
沈丽丽,王 莹
基于奇异值分解的无参考立体图像质量评价
沈丽丽,王 莹
(天津大学电气自动化与信息工程学院,天津 300072)
针对非对称失真立体图像,提出了一种基于奇异值分解的无参考评价算法.该方法首先考虑人眼对空间频率变化敏感的特性和双目融合特性,对立体图像进行Gabor滤波,基于奇异值分解的融合策略生成融合图.然后,采用亮度加权直方图的局部二值模式算法分别对融合图、左右子图像提取特征,并将左右子图像的特征向量融合、采用欧几里得距离和夹角余弦进行向量之间的比较;为度量非对称失真差异,利用图像相似度算法计算左右子图像之间的相似性.最后,将融合图的特征向量、子图像的融合及比较特征向量、子图像的相似度特征向量级联,利用支持向量回归(SVR)算法完成特征到主观质量分数的回归映射.在LIVE 3D Ⅱ、Waterloo-IVC Ⅰ和Waterloo-IVC Ⅱ立体图像库上对本算法进行测试.实验结果表明,本算法性能良好,优于目前主流的立体图像质量评价算法.
立体图像质量评价;非对称失真;奇异值分解;欧几里得距离;图像相似度
在立体图像处理过程中,创建、压缩、传输、重建、渲染和显示这些步骤都难免在原始图像上引入各种失真[1].因此,需要对立体图像进行图像质量评价(image quality assessment,IQA).立体图像质量评价可分为主观评价和客观评价方法.然而主观评价耗时且计算复杂,因此,急需一种有效的客观3D-IQA方法用来评价立体图像的质量.
在立体图像质量评价领域,早期的方法直接将平面图像质量评价算法如BRISQUE[2]、BLIINDS-Ⅱ[3]算法,分别应用到左右图像得到左右图像的质量分数,将两个分数的平均值作为立体图像的分数.这些方法没有考虑到双目视觉特性,如双目竞争、双目融合、图像的深度信息,因此评价效果不甚理想.为了更好地模拟立体视觉机制,文献[4]考虑了立体视差,然后将平面评价算法应用到立体图像和视差图上.文献[5]考虑了双眼视觉特性,并提出一种全参考评价模型.然而原始图像在实际应用中难以获取,无需原始图像的无参考(no-reference,NR)立体图像质量评价逐渐成为研究热点.
文献[6]将提取的左右图像的2D特征结合起来,然后结合主观质量分数(MOS或DMOS)进行回归预测,得到立体图像的质量分数.Chen等[7]依据双目竞争原理,提出了Cyclopean(融合图)模型.Chen等[8]基于上述模型,结合视差图、不确定图,分别提取2D特征和3D特征.文献[9]提取了收敛融合图的自然场景统计(natural scene statistics,NSS)特征用于无参考质量评价.Yue等[10]分析了NSS、结构和失真对称性,提出多尺度亮度归一化的预处理方法,计算左右图像的梯度相似性来量化非对称失真.文献[11]考虑双目视觉特性和局部视觉结构特性,计算双目竞争响应和双目方向选择的自相似性来表征失真立体图像的质量.
上述客观质量评价算法与人眼对图像的主观感知有着较高的一致性.然而在评价非对称失真立体图像时,这些客观算法的效果欠佳.立体图像质量评价要考虑多方面因素,包括图像的多失真、不一致的视点感知、深度信息和视觉不适[12-13].尤其是当左视图和右视图因为受到不同的失真类型或失真程度的刺激时,即非对称失真的立体图像,便会具有不同的视觉感知质量,此时立体图像质量评价更加充满挑 战性.
本文针对非对称失真立体图像,采用基于奇异值分解的融合策略对左右图像、左右图像的特征向量分别进行像素级和特征级融合;利用特征向量比较和图像相似度算法去量化左右图像的非对称失真.实验结果表明在非对称失真立体图像库上,算法有着较高的预测准确性.
1 立体图像质量评价模型
本文所提出的基于奇异值分解的无参考立体图像质量评价算法,框图如图1所示.步骤1:利用Gabor滤波器将左右图像分解为3对不同空间频率下的左右子图像.步骤2:基于奇异值分解的融合策略得到融合图以表征双目融合信息;然后用亮度加权直方图的局部二值模式(luminance-eighted histogram local binary pattern,LWH-LBP)特征提取算法分别提取融合图、左子图像、右子图像的特征,并将左右子图像的特征向量进行融合和比较;针对非对称失真,利用图像相似度算法FSIM来量化左右子图像的差异;最后,将融合图的特征向量、子图像的融合及比较特征向量、子图像的相似度特征向量级联成一个总的特征向量.步骤3:利用支持向量回归(support vector regression,SVR)算法进行特征向量到主观质量分数的映射并客观预测立体图像的质量分数.

图1 算法框图
1.1 图像金字塔分解
人类视觉系统对空间频率变化的敏感特性可以用塔式Gabor变换来表示[14].本算法采用Gabor滤波器实现图像的金字塔分解,得到不同空间频率下的左右子图像.Gabor滤波器的数学模型为


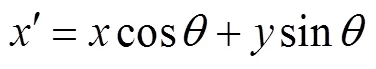
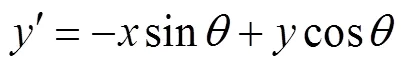
式中:()是图像中像素的空间坐标;(,)是旋转变换后的坐标;是波长系数;是方向系数;是带宽系数;是Gabor滤波器的波长系数;是相角偏移系数.为了平衡算法的准确性和复杂度,这里只设置不同的带宽系数而固定方向系数,得到3个尺度下的图像信息.参数设置为:=0°,={1.33,1.90,2.91}.立体图像经过Gabor分解,得到3对左右子图像l, gabor()(,)、r, gabor()(,),=1,2,3.
1.2 特征提取
1.2.1 双目融合
为了模拟立体图像通过人类视觉系统在人脑中形成具象过程,需要对双目融合特性进行建模.现有的立体图像质量评价算法对双目融合建模的方法有Cyclopean图方法[7]和Convergent Cyclopean图方 法[9].这些方法大多基于视差图算法,然而视差图算法尚未完善,因此融合效果不甚理想.
本算法采用一种基于奇异值分解的融合策略,并采用线性加权模型得到左右子图像的融合图.对×矩阵进行奇异值分解(singular value decomposition,SVD).由式(4)可知,奇异值可代表图像的能量信息,而图像的能量信息与图像的失真类型和失真程度有着高度的相关性[15].因此可以用图像矩阵的奇异值来表征失真图像,并且将左右子图像各自的奇异值之和作为线性加权的权重,表示为

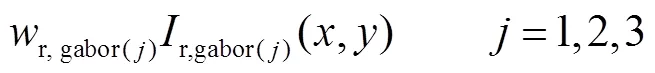

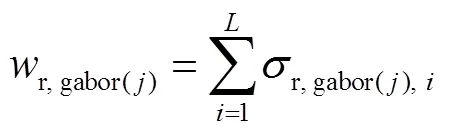
式中:运算符||·||E表示欧几里得范数;为方阵T的特征值;是矩阵的秩;σ是矩阵的奇异值;l,gabor()(,)和r,gabor()(,)分别表示第个尺度下Gabor滤波得到的左右子图像;C,gabor()(,)表示左右子图像叠加得到的融合图;l,gabor()和r,gabor()分别表示线性加权时左右子图像的权重;l,gabor(),和r,gabor(),分别表示左右子图像矩阵的第个奇异值,=1,2,…,.为直观显示融合效果,在LIVE 3D Ⅱ数据库中选取一幅立体图像,经过Gabor滤波器滤波得到一组左右子图像,将其叠加融合得到融合图,结果如图2所示.
1.2.2 图像特征提取算法
局部二值模式(local binary pattern,LBP)编码用来描述一幅图像邻域中的像素之间的关系,这样的微结构模式可以表征不同失真情况下的图像质量的下降[16].因此LBP算法可以用来度量各种失真类型的引入对图像质量的影响.LBP编码的计算过程如式(8)和(9)所示.

图2 滤波后的左右子图像及融合图
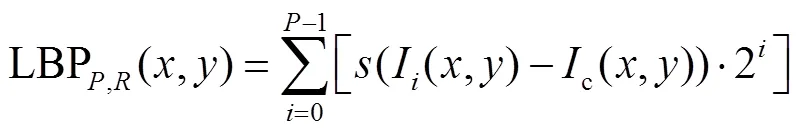

式中:表示中心像素的周围像素的个数;表示邻域的半径;c(,)和I(,)分别表示中心像素点和其邻近像素点的亮度值.为了使编码过程具有旋转不变性和提高LBP的识别不同模式的能力,可以采用旋转不变局部二值模式.具体实现时,=8,=1;得到+2个模式,即10个模式.不同的LBP模式代表着不同的局部亮度模式,比如模式0代表孤立的亮点,模式4代表不同正负曲率的边缘,模式8代表平滑区域或者暗点.
为了同时捕捉亮度和结构信息,本文采用亮度加权的直方图对亮度和结构信息进行融合,将具有相同局部二值模式的亮度值累加,用式(10)和(11)表示.然后对直方图归一化,用式(12)表示.
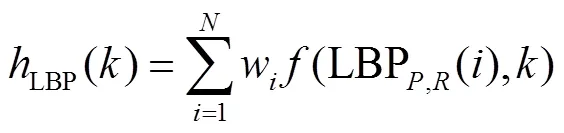
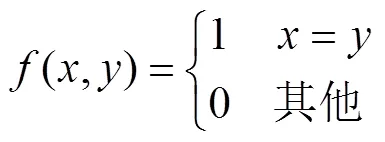
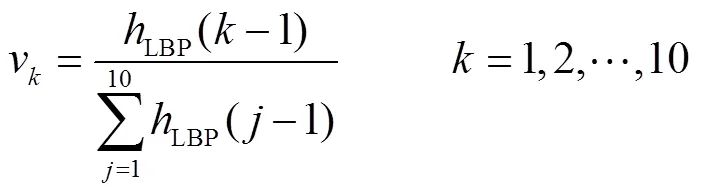
式中:表示图像像素个数;∈[0,]是不同的局部二值模式,的值为9;权重w为像素的亮度值(,),表示亮度值越大,所占比重越大;v表示特征向量的第个分量.
将上述改进的LBP算法称为亮度加权直方图的LBP(luminance-weighted histogram-LBP,LWH-LBP)算法.鉴于人类视觉多尺度特性,在3个尺度下对图像进行LBP编码.最终,LWH-LBP算法对一幅平面图像提取30维特征.为直观显示LBP编码结果,对图2中的融合图取图像块并进行LBP编码,结果如图3所示.图3(b)表示由(,)确定的像素点的模式值,用不同的颜色表示这10种模式.

图3 融合图图像块及LBP编码
1.2.3 特征融合和特征比较
为了保留左右子图像本身的信息,需提取左右子图像的特征.以下表述针对左右图像经过Gabor单一尺度分解得到的左右子图像,为简化起见,省略相关变量下标中的gabor().首先利用LWH-LBP算法对融合图进行特征提取,特征向量记为1.然后分别对左右图像进行特征提取,特征向量分别记为l、r.并将这两个特征向量融合和比较,融合权重仍取左右图像融合时的权值,即l和r,融合后的特征向量记为2,可表达为式(13).特征向量l、r之间的比较采用欧几里得距离和夹角余弦来度量两向量之间距离和方向上的差异.欧几里得距离和夹角余弦cosine计算式分别为式(14)、(15).、cosine的计算结果作为向量分量,组成一个新特征向量3.
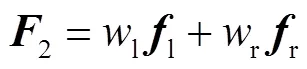

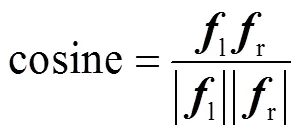
1.2.4 左右图像联合特征提取
非对称失真立体图像的左右图像之间在失真位置、失真类型或者失真程度上不同,因此可以提取左右图像的相似程度作为特征来表示这种差异.
本文采用FSIM算法[17]来衡量左右图像的相似程度.在FSIM算法中提取相位一致性(phase congruency,PC)和梯度幅度(gradient magnitude,GM)作为图像的结构特征.相位一致性可以表示图像的边缘和边角信息,利用Kovesi模型[18]计算左右图像的相位一致性.采用Scharr算子计算梯度.将FSIM的计算结果作为左右图像的联合特征,记为一维特征向量4.最后,将上述1、2、3、4拼接成一个总的特征向量,记为3D.
1.3 特征映射
为了得到客观的立体图像质量分数,利用回归模型来学习从特征空间到主观质量分数(DMOS或MOS)的映射关系.本算法采用支持向量回归算法(SVR)[19].SVR已被用于平面和立体图像质量评价领域[20-21]并帮助评价算法取得了良好的预测效果.SVR被用来处理高维数据和求解凸二次规划的最优化问题.在实现时采用林智仁教授开发的LIBSVM软件包;核函数采用默认的径向基函数(radial basis function,RBF).
2 实验结果及分析
2.1 数据库及算法评价指标
为了衡量本算法对非对称失真立体图像质量预测的性能,在LIVE 3D Ⅱ数据库、Waterloo-IVC Ⅰ和Waterloo-IVC Ⅱ数据库这3个立体图像数据库上进行训练和测试. LIVE 3D Ⅱ数据库包含8幅原始图像和5种失真类型;每种失真类型有9种失真程度,共计360幅失真图像.每幅立体图像对应一个主观质量分数(DMOS).Waterloo-IVC Ⅰ数据库包含6幅原始图像,3种失真类型,330幅失真图像.Waterloo-IVC Ⅱ数据库包含10幅原始图像,3种失真类型,460幅失真图像.这3个数据库均包含对称失真和非对称失真的立体图像,图像的失真情况较为复杂,因此是公认的具有挑战性的立体图像数据库.衡量立体图像质量评价算法性能常用的指标有Spearman等级相关系数(SROCC)、Pearson 线性相关系数(PLCC)、均方根误差(RMSE).将数据库中的失真图像随机分成训练集和测试集两部分,其中训练集占80%,测试集占20%,且这两部分无内容相同的图像.利用SVR进行训练然后测试,得到SROCC、PLCC和RMSE值,迭代1000次训练和测试过程,最后取1000次迭代结果的中值作为算法性能的衡量结果.
2.2 算法性能分析
为了评价本算法的预测性能,将本算法与其他一些全参考及无参考的立体图像质量评价算法进行了比较,结果见表1.从表1可以看出:本文算法在LIVE 3D Ⅱ、Waterloo-IVC Ⅰ和Waterloo-IVC Ⅱ这3个数据库上的总体性能均优于列出的其他算法,本文算法对于预测立体图像质量有着较高的准确性.在LIVE 3D Ⅱ数据库上,与其他算法相比,本文算法的3个性能衡量指标均最优,Yue等[10]的算法次之.在Waterloo-IVC Ⅰ和Waterloo-IVC Ⅱ数据库上,与其他算法相比,本文算法的SROCC和PLCC最高,RMSE最低,即本算法的预测准确性能最优.从表1还可以看出,列出的其他算法在LIVE 3D Ⅱ数据库上有着较好的性能表现,但是在Waterloo-IVC Ⅰ和Waterloo-IVC Ⅱ数据库上,这些算法表现欠佳.而本文算法在这3个含有非对称失真图像的数据库上均有着高准确性,因此本文算法的泛化能力最优.BRISQUE[2]和BLIINDS-Ⅱ[3]两种算法是平面图像质量评价算法,在评价立体图像,尤其是非对称失真立体图像时,由于没有考虑立体图像的特性,因此算法的效果不佳.Chen等[8]的NR算法在3个数据库上预测准确性较好,但是该算法生成融合图时利用立体匹配算法得到视差图,而现有的立体匹配算法有诸多不足,导致该算法在LIVE 3D Ⅱ数据库上的性能表现不够理想.Yue等[10]的算法在生成融合图时也存在同样的缺点.本文算法的融合策略并不依赖现有某种算法,且量化了左右图像的差异,因此在3个数据库上性能表现最佳.
表1 算法在LIVE 3D Ⅱ、Waterloo-IVC Ⅰ和Waterloo-IVC Ⅱ数据库上的整体性能
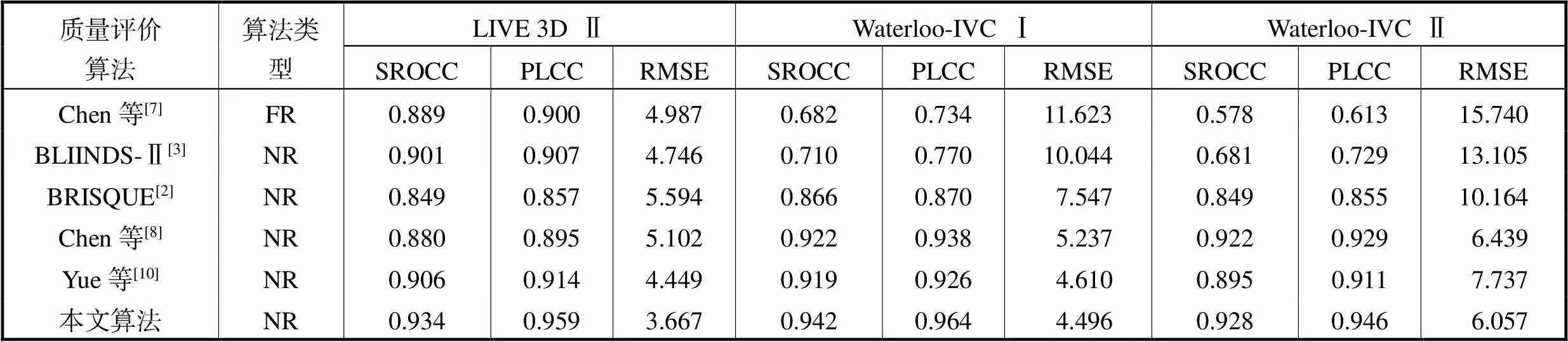
Tab.1 Overall performance of the algorithms in the LIVE 3D Ⅱ,Waterloo-IVC Ⅰ,and Waterloo-IVC Ⅱ databases
为了验证算法在不同失真类型图像上的性能,对单一失真类型图像进行训练和预测,实验结果如表2所示.表2列出了几种算法在LIVE 3D Ⅱ数据库的单一失真类型图像上的SROCC结果.从表2可以看出:算法在不同失真类型图像上的性能表现有所差异.Chen等[8]的NR算法在预测WN、BLUR和FF失真图像质量时有较高的准确性.Yue等[10]的算法在预测JP2K和WN失真图像质量时有较高的准确性.本文算法在预测JP2K、WN、BLUR和FF失真图像质量时均有较高的准确性.
表2 在LIVE3DⅡ数据库不同失真类型图像上的SROCC值
2.3 鲁棒性分析
为了验证本文算法的鲁棒性,在LIVE 3D Ⅱ数据库上设置不同的训练图像比例,依次为80%、60%、40%、20%.实验结果如表3所示,随着训练图像比例的增大,算法的性能表现越好.即使训练比例低到20%,算法的性能表现仍较好,PLCC值也能达到0.915.因此本文算法具有较好的鲁棒性.
表3 在LIVE3D Ⅱ上不同训练图像比例下算法性能的比较
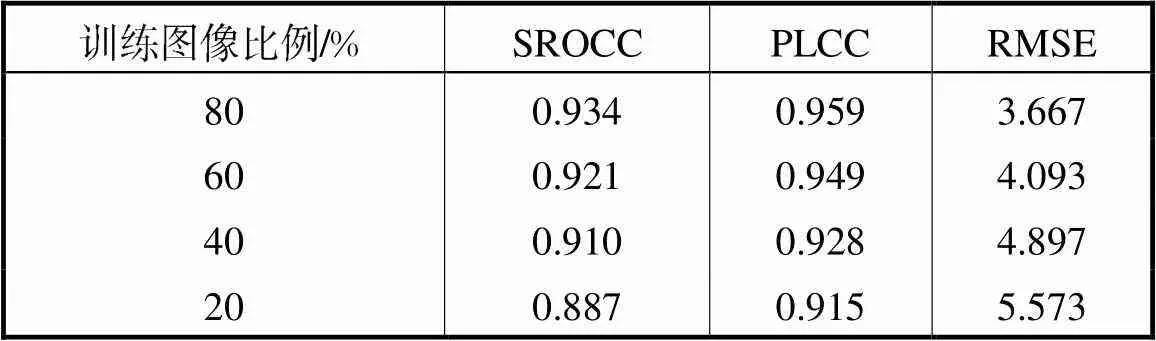
Tab.3 Performance comparison of the algorithms at various training ratios in the LIVE 3D Ⅱ database
3 结 语
本文提出了一种基于奇异值分解的无参考立体图像质量评价算法.考虑人眼的频率敏感性和双目融合特性,本算法利用基于奇异值分解的融合策略生成融合图;针对非对称失真图像,为度量左右图像之间的差异,提取了左右图像的相似度特征;在3个含有非对称失真立体图像的数据库上进行训练和预测.实验结果表明,本文算法对立体图像质量的预测有较高的准确性,且有较好的泛化能力和鲁棒性.
[1] Chang Y,Kim M. Binocular suppression-based stereoscopic video coding by joint rate control with KKT conditions for a hybrid video codec system[J]. IEEE Transactions on Circuits and Systems for Video Technology,2015,25(1):99-111.
[2] Mittal A,Moorthy A K,Bovik A C. No-reference image quality assessment in the spatial domain[J]. IEEE Transactions on Image Processing,2012,21(12):4695-4708.
[3] Saad M A,Bovik A C,Charrier C. Blind image quality assessment:A natural scene statistics approach in the DCT domain[J]. IEEE Transactions on Image Process-ing,2012,21(8):3339-3352.
[4] You J,Xing L,Perkis A,et al. Perceptual quality assessment for stereoscopic images based on 2D image quality metrics and disparity analysis[C]// 5th International Workshop on Video Processing and Quality Metrics for Consumer Electronics. Scottsdale,USA,2010:1-6.
[5] Shao F,Lin W,Gu S,et al. Perceptual full-reference quality assessment of stereoscopic images by considering binocular visual characteristics[J]. IEEE Transactions on Image Processing,2013,22(5):1940-1953.
[6] Shao F,Li K,Lin W,et al. Using binocular feature combination for blind quality assessment of stereoscopic images[J]. IEEE Signal Processing Letters,2015,22(10):1548-1551.
[7] Chen M J,Su C C,Kwon D K,et al. Full-reference quality assessment of stereopairs accounting for rivalry[J]. Signal Processing:Image Communication,2013,28(9):1143-1155.
[8] Chen M J,Cormack L K,Bovik A C. No-reference quality assessment of natural stereopairs[J]. IEEE Transactions on Image Processing,2013,22(9):3379-3391.
[9] Su C C,Cormack L K,Bovik A C. Oriented correlation models of distorted natural images with application to natural stereopair quality evaluation[J]. IEEE Transactions on Image Processing,2015,24(5):1685-1699.
[10] Yue G,Hou C,Jiang Q,et al. Blind stereoscopic 3D image quality assessment via analysis of naturalness,structure,and binocular asymmetry[J]. Signal Processing,2018,150:204-214.
[11] Zhou W,Zhang S,Pan T,et al. Blind 3D image qual-ity assessment based on self-similarity of binocular features[J]. Neurocomputing,2017,224:128-134.
[12] Kim D,Choi S,Sohn K. Visual comfort enhancement for stereoscopic video based on binocular fusion characteristics[J]. IEEE Transactions on Circuits & Systems for Video Technology,2013,23(3):482-487.
[13] Zhou W,Yu L,Zhou Y,et al. Blind quality estimator for 3D images based on binocular combination and extreme learning machine[J]. Pattern Recognition,2017,71:207-217.
[14] Campbell F W,Robson J G. Application of Fourier analysis to the visibility of gratings[J]. The Journal of Physiology,1968,197(3):551-566.
[15] Hu A,Zhang R,Yin D,et al. Image quality assessment using a SVD-based structural projection[J]. Signal Processing:Image Communication,2014,29(3):293-302.
[16] Ojala T,Pietikainen M,Maenpaa T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(7):971-987.
[17] Zhang L,Zhang L,Mou X,et al. FSIM:A feature similarity index for image quality assessment[J]. IEEE Transactions on Image Processing,2011,20(8):2378-2386.
[18] Kovesi P. Image features from phase congruency[J]. Videre:Journal of Computer Vision Research,1999,1(3):1-26.
[19] Schölkopf B,Smola A J,Williamson R C,et al. New support vector algorithms[J]. Neural Computation,2000,12(5):1207-1245.
[20] 李素梅,薛建伟,秦龙斌,等. 基于融合图像的无参考立体图像质量评价[J]. 天津大学学报:自然科学与工程技术版,2019,52(10):1055-1061.
Li Sumei,Xue Jianwei,Qin Longbin,et al. Non-reference stereoscopic image quality evaluation based on fusion image[J]. Journal of Tianjin University:Science and Technology,2019,52(10):1055-1061(in Chinese).
[21] 侯春萍,林洪湖. 基于网格与韦泊统计特性的立体图像质量评价[J]. 天津大学学报:自然科学与工程技术版,2018,51(10):1015-1022.
Hou Chunping,Lin Honghu. Stereoscopic image quality assessment based on grid and weibull statistics[J]. Journal of Tianjin University:Science and Technology,2018,51(10):1015-1022(in Chinese).
No-Reference Stereoscopic Image Quality Assessment Based on Singular Value Decomposition
Shen Lili,Wang Ying
(School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China)
For asymmetrically distorted stereoscopic images,a no-reference evaluation algorithm based on singular value decomposition is proposed.First,considering visual sensitivity to spatial frequency variation and binocular fusion,Gabor filtering was performed on the stereoscopic image,and a fusion strategy based on singular value decomposition was proposed to generate a cyclopean image of the left and right sub-image pair.Then,the proposed luminance-weighted histogram local binary pattern metric was used to extract features of the cyclopean image and the left and right sub-images.Furthermore,feature fusion and comparison were conducted on the two feature vectors corresponding to the left and right sub-images,respectively.Euclidean distance and cosine were used to implement the vector comparison.Particularly,to measure the difference between asymmetrically distorted sub-image pair,image similarity metric was utilized to calculate the similarity between the left and right sub-image pair.Finally,feature vector of the cyclopean image,the fusion and comparison feature vectors,and the similarity feature vector were concatenated into a total feature vector,and regression mapping was performed from the feature vector to the subjective score using support vector regression.The algorithm was tested on the LIVE 3D Ⅱ,Waterloo-IVC Ⅰ and Waterloo-IVC Ⅱ databases.The experimental results show that the proposed algorithm has an outstanding performance and is superior to other state-of-the-art image quality assessment metrics.
stereoscopic image quality assessment;asymmetric distortion;singular value decomposition;Euclidean distance;image similarity
TN919.8
A
0493-2137(2020)06-0641-06
10.11784/tdxbz201903054
2019-03-25;
2019-04-16.
沈丽丽(1978— ),女,博士,副教授.
沈丽丽,sll@tju.edu.cn.
国家自然科学基金资助项目(61520106002).
Supported by the National Natural Science Foundation of China(No.61520106002).
(责任编辑:王晓燕)

