涌潮水流作用下桩柱表面压强及受力分析
张芝永,肖厅厅,戚 蓝,陈 刚,曾 剑
涌潮水流作用下桩柱表面压强及受力分析
张芝永1,肖厅厅2,戚 蓝2,陈 刚1,曾 剑1
(1. 浙江省水利河口研究院浙江省河口海岸重点实验室,杭州 310020;2. 天津大学水利工程仿真与安全国家重点实验室,天津 300354)
涌潮水流是一种蕴含较大能量的强非线性间断流.针对我国钱塘江河口地区范围内桥墩等桩式建筑物在涌潮水流作用下长期遭受的猛烈冲击问题,采用物理模型试验对桩柱在潮前水深上下两部分表面压强时程变化及涌潮潮头最大冲击压强出现位置进行了探讨并拟合得到最大冲击压强计算公式;采用数值模拟手段进行分离式建模,对桩柱在潮前水深上下两部分受力进行提取分析并拟合得到涌潮作用力计算公式.研究结果表明,涌潮水流与桩柱相互作用过程可分为3个阶段:在瞬时冲击期内,潮前水深以上桩柱部分在潮头猛烈冲击作用下,桩柱表面压强及受到的作用力瞬间增大至极大值,潮前水深以下部分表面压强和受到的作用力增长缓慢;衰减振荡期内,桩柱在潮前水深以上部分表面压强和受到的作用力迅速下降,潮前水深以下部分压强波动不大,受到的作用力衰减速率明显小于潮前水深以上部分;绕流作用期内,桩柱在潮前水深上下两部分表面压强和受力波动逐渐减小.桩柱在涌潮作用下表面压强及受力大小与涌潮水流参数中的潮前水深0和落潮流速0呈负相关,与涌潮高度呈正相关;涌潮作用下最大冲击压强出现在0.5附近,拟合得到的最大冲击压强及作用力计算公式经验证后具有良好的精度,可为相关应用提供参考.
涌潮;桩柱;表面压强;作用力;经验公式
涌潮又称“怒潮”、“暴涨潮”,常产生于潮差较大的喇叭形海湾和河口中,是一种水位、流速急剧变化的涨潮潮波前锋线.涌潮在传播过程蕴含着巨大的能量,其水体内部紊动特性强烈,尤其是涌潮潮头传播以后的水体其水位和流速依旧较大,即俗称的“快水”阶段,涌潮水流的水力特性已有大量学者[1-3]展开研究,但是目前对于涌潮作用下桩柱式建筑物表面压强及作用力变化的研究成果还比较少.
涌潮蕴藏着巨大的能量,是一种难得的自然奇观,但同时又对涉水建筑物冲击破坏严重.对于涌潮作用力的研究,国内外学者通常将涌潮作为一种浅水长波或驻波,然后利用相应理论计算涌潮作用力.邵卫云等[4]通过对钱塘江六桥桥墩实测压力分析认为涌潮作用力可采用浅水长波理论和驻波理论公式,运用水力学理论公式和Morison公式得到的计算值与实测值相差较大.陈海军等[5]参考破碎波冲击桩柱的作用力计算方法,引入卷曲系数计算涌潮冲击力.杨火其等[6]和Arnason等[7]利用物理模型试验结果拟合出涌潮作用力计算经验公式.Bhalerao等[8]详细介绍了海啸波对海岸附近大型结构建筑物产生的作用力种类.St-Germain等[9]利用数值模拟研究了海啸对柱体结构的冲击过程,分析了不同海啸参数下作用力的变化情况.目前学者对涌潮潮头冲击作用下桩柱表面最大压强出现位置的探索较少,同时对桩柱在潮前水深以下或以上不同部位在涌潮水流作用下的时程响应对比也鲜见报道.
涌潮作用下,涌潮冲击压强的分布特征及其整体受力对结构物的局部破坏及整体稳定有重要影响.对于最大压强分布情况,本文采用物理试验来对涌潮水流引发的桩柱迎流面压强变化进行分析,对涌潮潮头最大冲击压强出现位置进行探讨并拟合出最大冲击压强计算公式;对于桩柱受力情况,由于压力测点无法覆盖整个桩柱表面,无法对其受力进行物理试验分析,因此本文采用数值模拟的方法,对桩柱在涌潮作用下的受力时程变化进行了计算分析,并得到了涌潮作用力计算公式,其研究结果可为实际工程提供参考.
1 研究方法
1.1 物理模型试验
试验在浙江省水利河口研究院六堡试验基地多功能涌潮水槽中进行,试验所用水槽长50.0m,宽3.0m,高1.2m.为了保证涌潮水流传播至桩柱局部时涌潮潮头已充分发展且水槽下游末端反射对试验过程的影响尽量小,将试验区域布置在水槽中部,整体试验布置如图1所示.

每组试验开始时都对传感器采集仪进行初始化调零,因此本次试验中处于潮前水深以下的各传感器所测到的压强值已去除涌潮尚未产生时测点处的相应的静水压强.
涌潮试验按弗劳德数相似准则进行设计,模型几何比尺为1∶30,对应于钱塘江天然涌潮水流条件为潮前水深0为2.1~6.9m、涌潮高度为1.8~3.3m的波状涌潮和旋滚涌潮,共进行20组试验.水槽两端分别安装有多台潜水泵,试验过程中通过测控系统首先调节水槽中水位恒定并使落潮流速0为0m/s,随后通过增加水槽一端水泵运行频率进而在水槽中产生试验所需涌潮水流.
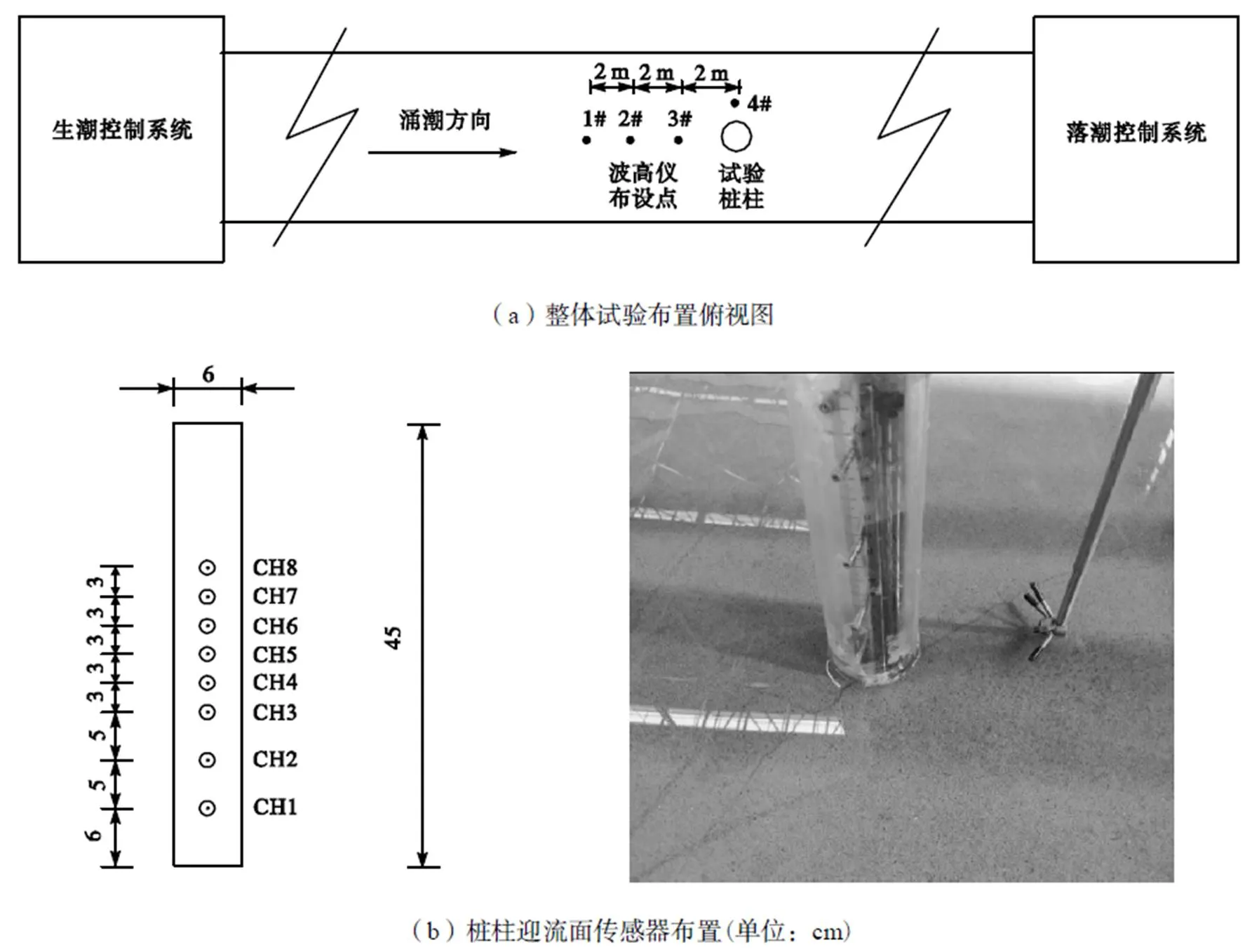
图1 物理试验模型布置
1.2 数值模拟
1.2.1 数学模型简介
本节采用数值模拟的手段对涌潮作用力进行提取,数学模型的基本控制方程为连续性方程和动量方程[10],即
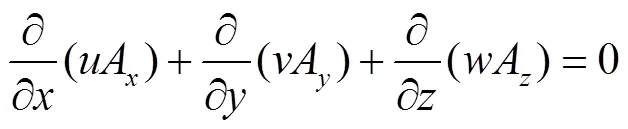
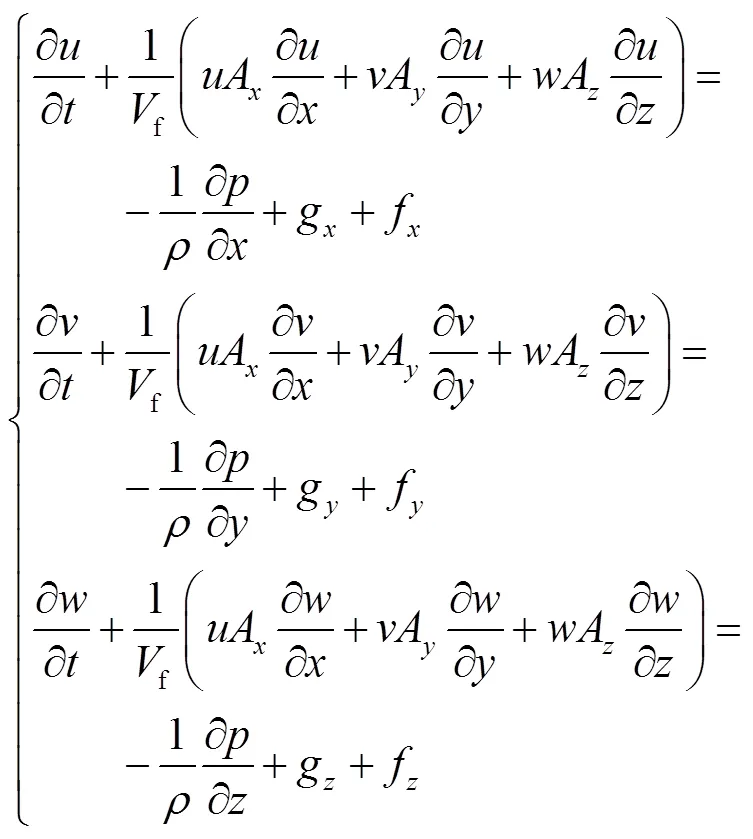
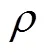
由于在模型中使用溃坝机制产生涌潮水流过程,较难对所需要的涌潮水流条件进行控制,本次模型中在模型边界处通过赋予基于理论公式推导得出的涨潮水位和流速进而产生所需要的涌潮水流,该模型用以产生涌潮水流的科学性和有效性已得到验证,由于篇幅所限,关于本模型的更多介绍可以参考文献[11]中的相关内容.
1.2.2 模型准确性验证
首先对数学模型中关于桩柱受到的水流作用力过程进行捕捉准确性检验.
采用文献[7]的水槽试验数据进行验证,试验所用水槽长16.60m,宽0.60m,高0.45m,水槽左端布置隔水挡板进行水箱蓄水,水槽中部位置放置截面为0.12m´0.12m的试验桩柱,初始水垫层厚度为0.02m.试验过程中通过抽取隔水挡板使水流以溃坝波的形式对试验桩柱进行冲击.
数值模拟计算得到的模拟值和试验值进行对比,如图2所示,从图中可以看出本文采用的数值模拟方法对涌潮作用力的捕捉具有较好的精度,数值模拟得到的涌潮作用力变化过程与试验结果基本相同,作用力数值最大误差不超过5%.说明本文所建数学模型可用于溃坝波等急速冲击水流过程中的水动力模型计算,同样也适用于与溃坝波类似的涌潮冲击结构物的水动力模型计算.
利用该数学模型对潮前水深0为0.04~0.23m、涌潮高度为0.03~0.11m、圆柱直径为0.06m的组合工况下的圆柱受力过程进行模拟计算.
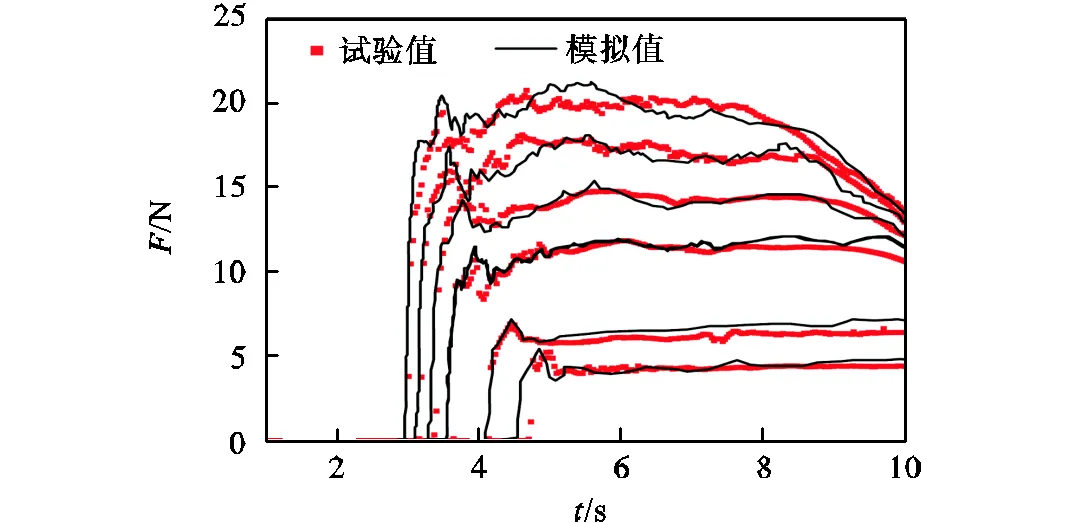
图2 溃坝波作用力过程模型验证
2 结果分析与讨论
2.1 桩柱表面压强分析
通过物理试验得到圆柱表面各测点压强变化过程如图3所示,代表涌潮过程中涌潮高度变化情况.从图3可以看出涌潮作用下桩柱表面压强与水深波动基本保持一致,这种现象在波状涌潮工况下尤为明显.
位于潮前水深以下的测点处压强变化的起增时刻与水位变化保持同步,潮前水深以上测点压强起增时刻稍晚于潮前水深以下测点且越往上测点压强变化滞后越久,出现这种现象的原因是因为潮头具有一定陡度,因此涌潮波接触桩柱不同高度的时间存在一些差距.从整体上看,在潮前水深0保持一定时,随着涌潮高度的增加,各测点处的压强波动也相应地增加.
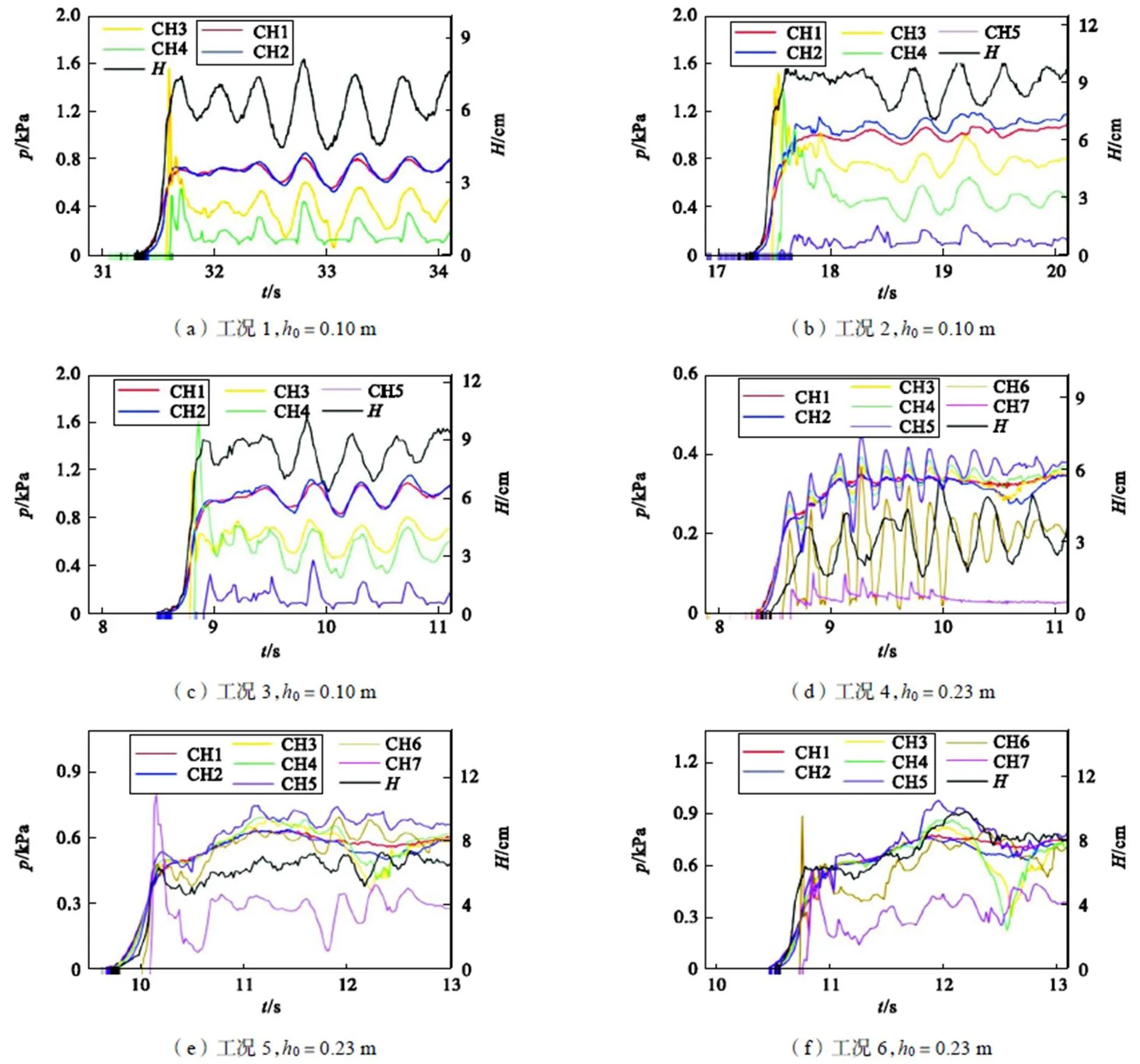
图3 涌潮过程中各测点压强变化(黑框中测点位于潮前水深以下)
从图3中可以发现,涌潮水流作用下桩柱表面潮前水深以下各测点压强普遍没有潮前水深以上测点处的压强大,但是潮前水深以下测点处压强波动比潮前水深以上测点小.潮前水深以下测点压强在初始阶段增加到某一极值后增加速率减缓,随后又继续增加至某一较大值,但是这个特点在波状涌潮下体现得不明显.出现这种现象的原因是由于当潮前水深以下测点达到初始阶段的最大值时,潮头部分水体仍处于沿桩柱表面向上爬升及向下潜入的阶段,在此过程中,由涌潮高度部分水体带来的水体静水压强还未作用到潮前水深以下水体.在冲击压强回落阶段,桩柱迎水面爬升的水体在重力作用下下落,同时由于相应静水压力的叠加导致潮前水深以下测点压强继续增加.波状涌潮由于冲击作用相对较弱且由于水面波动具有周期性的特点,从而导致这种由壅高部分水体及下潜流带来的静水压强叠加效应并不明显,但是要说明的是整个过程的持续时间很短.潮前水深以下各测点之间压强波动比较接近,但要注意的是从图中可以发现越接近底部的测点其压强波动越小,说明涌潮水流作用下桩柱表面压强不同于静水压强分布,而是自底向上越接近自由水面其压强波动越大.
对于潮前水深以上部分来说,当涌潮潮头锋面触及桩柱表面一瞬间时水质点速度接近或等于零,此时速度变化率即加速度较大,依据能量守恒定律可知此时这部分水体的动能将转化为冲击荷载的形式作用于桩柱,因此潮头水体测点压强在短时间迅速增加至最大值后又急剧衰减,这一过程中波状涌潮衰减幅度相对于旋滚涌潮衰减幅度要大.这是因为潮前水深以上测点所测到的初始压强极值应是涌潮潮头水流的冲击压强,随后在桩柱阻水作用下桩柱迎水面局部流速减缓并出现局部回头潮现象从而导致迎水面中心线处流速反向,也就导致其表面受到的压强衰减,而波状涌潮由于水面波动的涨落潮周期性导致落潮阶段水深减小幅度较大,从而在整体上导致压强衰减幅度大.随着后续涌潮波的继续传播,迎水面局部水体又被裹挟对桩柱进行冲击,从而导致桩柱表面压强增加,但是可以发现此后桩柱表面压强所能达到的极值没有初始阶段的冲击压强大.
2.2 桩柱表面冲击压强计算公式
从上面的分析可以发现在整个涌潮过程中,桩柱表面所受到的压强一直在不停波动,除此以外从各测点的压强极值分布来看,潮前水深以上测点压强最大值出现在涌潮高度中部位置,并不是在接近潮前水深或潮头顶部的测点处,下面将对最大冲击压强出现位置进行探讨.
从图3中可以发现,波状涌潮作用下潮前水深测点处冲击压强比潮前水深以上测点处压强要大,考虑到天然河道中的涌潮形态以旋滚涌潮为主,因此下面仅对旋滚涌潮下潮前水深以上水体部分的冲击压强进行分析.
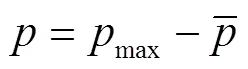
为了更好地研究涌潮潮头的冲击特性,采用无量纲水深进行描述,
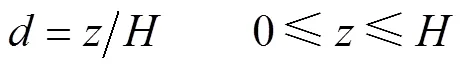
式中为测点距潮前水深的距离.
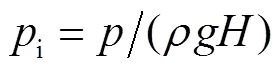
图4为各测点下无量纲水深和无量纲冲击压强分布,从图4可以看出涌潮潮头最大冲击压强位置出现在0.5H附近,并且最大冲击压强不超过涌潮高度部分水体引起的静水压强的1.2倍.
关于涌潮压强分布的情况,在目前公开发表的文献[5,12-13]中指出潮前水深处的压强值最大,涌潮压强中的脉动分量最大值出现在潮头锋面碰撞桩柱时刻,测得的压强最大值比碰撞时刻滞后约2.5s,这和文献中用以分析的涌潮压强值同时包含静水压强和动水压强两部分是密切相关的.涌潮潮头锋面在碰撞桩柱时涌潮波内部流速最大时产生的冲击作用更强,而在2.5s后流速已经明显衰减但涌潮水流中潮前水深以上水体比底层水体内部流速要大.本文分析的仅为桩柱在潮前水深以上部分所受到的涌潮冲击压强分布,从图3中潮前水深以上测点的压强变化情况也能明显发现压强极值是瞬时出现的,因此认为本文进行分析所用的此时所测得的压强值并不包含由涌潮波带来的水位上涨引发的静水压强,而前人进行压强分布分析时所用的压强值中有可能静水压强所占比重较大,因而在最后得到的压强分布与本文得到的冲击压强分布存在差异,相比之下本文得到的冲击压强位置分布更为准确.
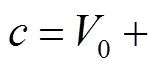
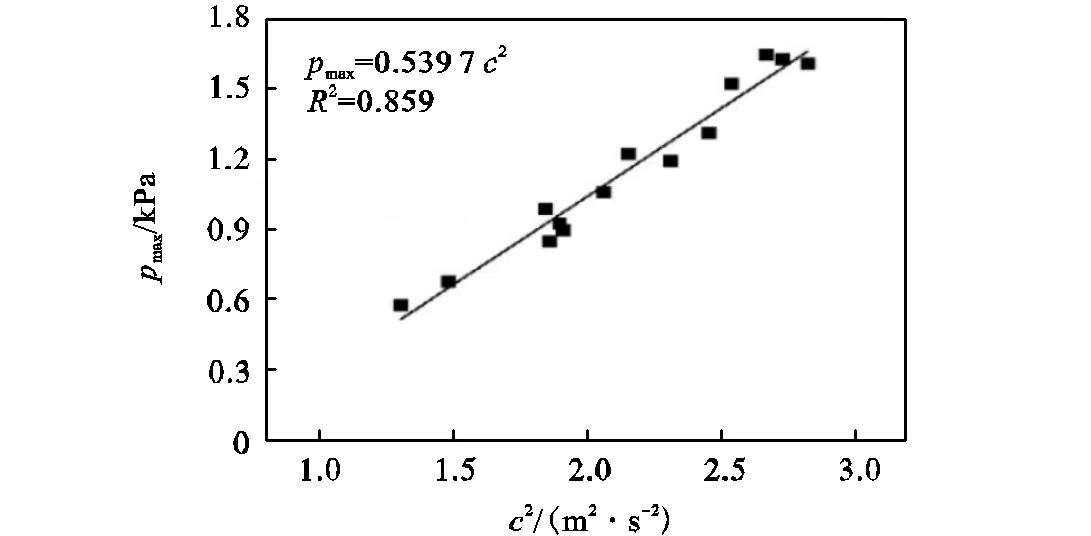
图5 涌潮冲击压强计算公式拟合
最终得到最大涌潮潮头冲击压强
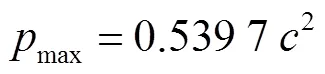
式(6)的2=0.859.
2.3 涌潮作用力特性分析
利用数学模型对20组涌潮-圆柱作用过程进行了模拟计算.涌潮过程中桩柱在潮前水深上下两部分受到的作用力机制是不同的,桩柱上半部分受力主要以冲击力为主,桩柱下半部分除了冲击力之外还受到绕流力作用.为了对这两部分力分别提取,本文选择在潮前水深0处将桩柱进行分离式建模,从而对柱体在潮前水深0以上部分受到的作用力U及潮前水深0以下部分作用力D进行提取,然后将两部分作用力进行相加作为桩柱受到的总力.
从图6所示的桩柱受力时程变化曲线上来看,涌潮作用下桩柱受力可分为瞬时冲击期、衰减振荡期、绕流作用期3个阶段.对于桩柱在潮前水深以上的部分,其受到的涌潮作用力在初始阶段短时间内上升到极值然后迅速衰减,这部分作用力为涌潮高度部分的涌潮波所带来的冲击力;衰减过程的持续时间随着数增加相应减小,其原因是由于数增加时后续涌潮水流的水力特性和碰撞时的那部分涌潮波的水力特性比较接近,所以在较短时间内又能对桩柱造成二次冲击,数较小的波状涌潮潮头后续部分水流为落潮流,此时无论是流速还是水深都小于潮头水流,要等到下一周期的涨潮流对桩柱进行冲击才会出现新的作用力峰值,此时的作用力同时包含了涌潮冲击力和绕流力两部分.对于桩柱在潮前水深以下的部分,由于涌潮潮头将要且尚未冲击桩柱时,桩柱局部已经有了一定流速,因此桩柱受到涌潮作用过程中绕流力将一直存在,其出现的第1个作用力峰值中涌潮冲击力所占比重较大,通过比较作用力回落幅度发现这一比重随数的减小而增大.

图6 涌潮作用下桩柱受力变化
通过对比上下两部分桩柱受力的时程变化可以发现潮前水深以下部分桩柱受力从第1个衰减阶段持续时间普遍长于潮前水深以上部分,在这个衰减阶段内绕流力所占比重逐渐增大.从各阶段持续时间来看,桩柱在潮前水深以上部分受力变化速率都大于潮前水深以下部分受力变化,这点在数较小的波状涌潮下更明显.
从图6可以发现,对于涌潮水流而言,当潮前水深0保持不变时,涌潮高度越大其数越大,此时涌潮水流对桩柱作用力的大小与数呈正相关;当涌潮高度一定时,潮前水深0越大其数越小,此时涌潮水流对桩柱作用力的大小与数呈负相关.两种涌潮条件下出现规律相反的原因在于第2种涌潮条件下,虽然水流数偏小,但是涌潮水流具备的流速依旧较大,这点从图中各工况下涌潮作用力响应时间的先后有所反映,涌潮波具备的传播速度越大,那么涌潮波内部蕴含的能量也更加强劲,在遇到阻碍时对桩柱产生的冲击效果也越强,因此在较大的涌潮传播速度作用下涌潮波对桩柱产生的作用力也就越大.旋滚涌潮条件下涌潮作用力变化情况如图7所示.
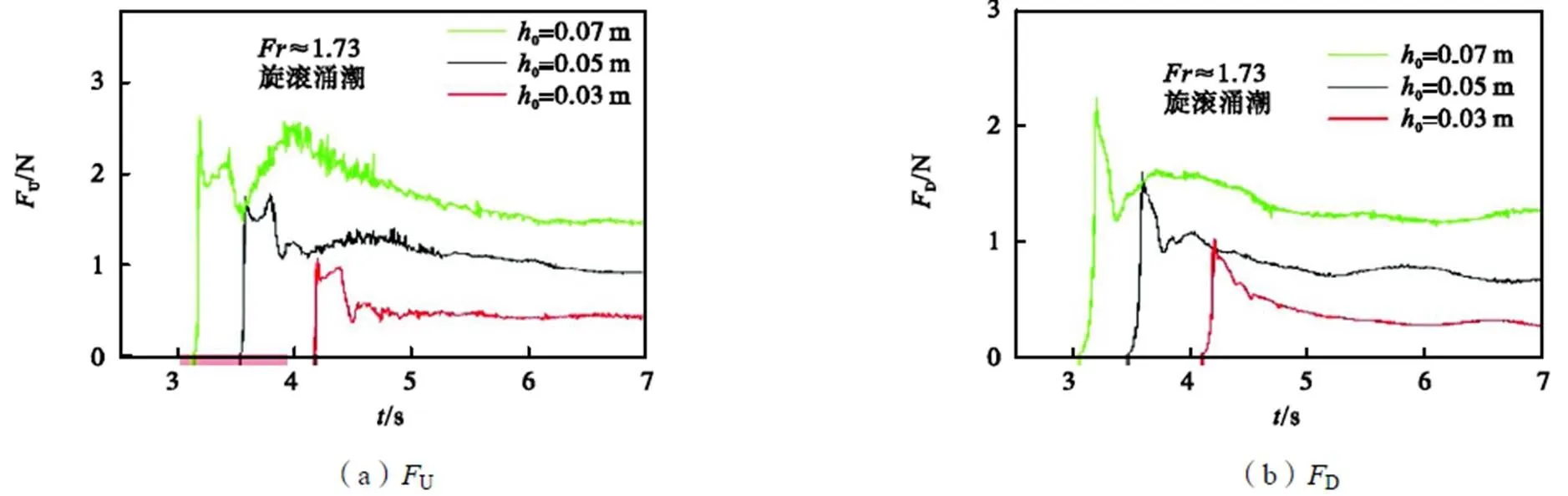
图7 旋滚涌潮形态下桩柱受力变化
从图7可以明显看出,当数保持一定时,涌潮作用下桩柱受力与涌潮传播速度呈正相关,此外戚蓝等[11]研究发现落潮流速0与涌潮传播速度呈负相关,因此当涌潮水流条件一定时,落潮流速0与涌潮作用力大小呈负相关.但是要说明的是从桩柱受力变化平稳的阶段来看,涌潮水流水深越大,其受到的作用力越大,这是因为此时涌潮作用力组成中冲击力已经很小,作用力以绕流力为主,在其余条件基本相同时,绕流力随水体流速及水体深度的增加而增加.
2.4 涌潮作用力计算公式
从前面分析中可以发现,涌潮对桩柱产生作用力的大小与传播速度呈正相关,而桩柱受到的作用力大小又和桩柱的受力面积有关,因此需要在计算公式中出现能反映受力面积的参数.
桩柱在涌潮作用下迎水面受力面积为一矩形面,该作用面的宽度即为桩柱直径的大小,作用面的高度为涌潮波作用过程中整个水体高度,传播速度与涌潮水体高度明显相关,因此在公式中考虑加入桩柱直径后与传播速度的平方建立关系,如图8所示.从图8可以看出涌潮作用下桩柱受力与2相关性良好,拟合得到的涌潮作用力计算式为
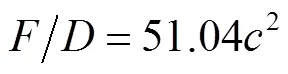
式(7)的R2=0.947.
为了检验上述得到的参数取值范围对涌潮作用力进行计算的可行性,利用钱塘江机场快线跨江大桥桩柱涌潮作用力试验资料进行验证,验证结果如图9所示,利用公式得到的计算值和试验值最大误差不超过15%,可认为本文得到的公式具有良好的准确性.
目前文献[15-16]关于破碎波、海啸波这类强非线性流对桩柱产生的作用力计算手段中常用的计算公式如下.

图9 作用力计算公式准确性验证
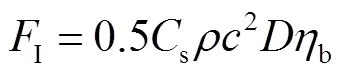
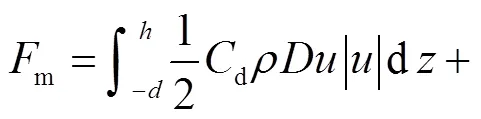
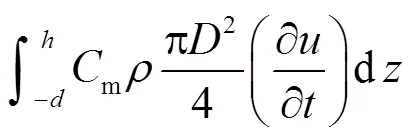
使用上述公式进行计算时不可避免地需要对其中的参数s、d等进行取值,不同的研究者关于各参数的取值也是基于各自试验结果进行反推拟合,暂时没有统一的认识,这其中针对涌潮水流展开的研究成果也比较少.此外在使用Morison公式时涌潮水流流速(非传播速度)更是难以用解析式进行计算,而本文建立的公式仅需在较容易实测得到的传播速度的基础上即可进行计算,相对实用性更好.
3 结 论
本文利用物理试验和数学模拟相结合的方法对涌潮作用下桩柱表面压强分布特征及整体受力特性进行研究分析,得到如下结论.
(1) 物理试验结果表明涌潮作用下桩柱在潮前水深以上部分受到的冲击压强最大,最大冲击压强出现在0.5附近;潮前水深以下部分压强波动幅度比潮前水深以上部分小.
(2) 落潮流速0与桩柱表面压强波动及受到的作用力呈负相关,潮前水深0一定时,涌潮高度越大时桩柱表面受到的压强和作用力越大,涌潮高度一定时,潮前水深0越小桩柱表面受到的压强和作用力越大.
(3) 物理试验和数值模拟结果表明涌潮作用下桩柱表面压强及受力变化可分为瞬时冲击期、衰减振荡期、绕流作用期3个阶段,第1阶段内潮前水深以上部分压强和受力的变化速率比潮前水深以下部分快,第2阶段衰减速率正好相反,总体来说潮前水深以下部分在涌潮过程中表面压强和受到的作用力波动幅度不大.
(4) 通过拟合得到的涌潮最大压强和作用力计算公式,经验证具有良好的精度,可为类似研究提供参考.
[1] Li Y,Pan D,Chanson H,et al. Tidal bore progressing on a small slope[J]. Experimental Thermal and Fluid Science,2017,88:513-518.
[2] Huang J,Pan C,Kuang C,et al. Experimental hydrodynamic study of the Qiantang River tidal bore[J]. Journal of Hydrodynamics,2013,25(3):481-490.
[3] Leng X,Chanson H,Reungoat D. Turbulence and turbulent flux events in tidal bores:Case study of the undular tidal bore of the Garonne River[J]. Environmental Fluid Mechanics,2018,18(4):807-828.
[4] 邵卫云,毛根海,刘国华. 钱塘江涌潮压力的动态测试与分析研究[J]. 浙江大学学报:工学版,2002,36(3):247-251.
Shao Weiyun,Mao Genhai,Liu Guohua. Dynamic measurement and analysis of the pressure in the Qiantangjiang Bore[J]. Journal of Zhejiang University:Engineering Science,2002,36(3):247-251(in Chinese).
[5] 陈海军,严 盛,徐长节,等. 直立方桩上涌潮压力动态测试及分析研究[J]. 水动力学研究与进展:A辑,2006,21(3):411-417.
Chen Haijun,Yan Sheng,Xu Changjie,et al. Dynamic measurement and study of the bore pressure on a vertical square cylinder in Qiantang River[J]. Journal of Hydrodynamics:Ser A,2006,21(3):411-417(in Chinese).
[6] 杨火其,卢祥兴,周建炯,等. 涌潮对垂直方柱正向作用力试验研究[J]. 水电能源科学,2008,26(3):118-119.
Yang Huoqi,Lu Xiangxing,Zhou Jianjiong,et al. Laboratory study for tidal bore acting force on vertical square cylinders[J]. Water Resources & Power,2008,26(3):118-119(in Chinese).
[7] Arnason H,Petroff C,Yeh H. Tsunami bore impingement onto a vertical column[J]. Journal of Disaster Research,2009,4(6):391-403.
[8] Bhalerao S B,Soni R S,Basu S. Study of forces generated on the structures due to tsunami loading[C]// Proceedings of the International Symposium on Engineering Under Uncertainty:Safety Assessment and Management(ISEUSAM-2012),2012:887-903.
[9] St-Germain P,Nistor I,Townsend R,et al. Smoothed-particle hydrodynamics numerical modeling of structures impacted by tsunami bores[J]. Journal of Waterway,Port,Coastal,and Ocean Engineering,2014,140(1):66-81.
[10] 尤学一,李 占. 黏性水波场和水平方柱波浪载荷的数值模拟[J]. 天津大学学报,2009,42(3):243-247.
You Xueyi,Li Zhan. Numerical simulation of viscous wave field and wave force on horizontal square cylinder[J]. Journal of Tianjin University,2009,42(3):243-247(in Chinese).
[11] 戚 蓝,肖厅厅,张芝永,等. 涌潮水流CFD数值模拟[J]. 水利水运工程学报,2019(3):32-40.
Qi Lan,Xiao Tingting,Zhang Zhiyong,et al. Numerical simulation of tidal bore based on CFD method[J]. Hydro-Science and Engineering,2019(3):32-40(in Chinese).
[12] 邵卫云,毛根海,刘国华. 钱塘江涌潮压力的分析与研究[J]. 水动力学研究与进展:A辑,2002,17(5):604-610.
Shao Weiyun,Mao Genhai,Liu Guohua. Analysis of
pressure in Qiantangjiang tidal bores[J]. Journal of Hydrodynamics:Ser A,2002,17(5):604-610(in Chinese).
[13] 李 颖,潘冬子,潘存鸿. 强潮河口桥墩涌潮压力试验研究[J]. 海洋工程,2017,35(4):53-58.
Li Ying,Pan Dongzi,Pan Cunhong. Experimental study of tidal bore-induced pressures on piers in a macro-tidal estuary[J]. The Ocean Engineering,2017,35(4):53-58(in Chinese).
[14] 潘存鸿,鲁海燕,曾 剑. 钱塘江涌潮特性及其数值模拟[J]. 水利水运工程学报,2008(2):1-9.
Pan Cunhong,Lu Haiyan,Zeng Jian. Characteristic and numerical simulation of tidal bore in Qiantang River[J]. Hydro-Science and Engineering,2008(2):1-9(in Chinese).
[15] Alagan C M,Bihs H,Myrhaug D,et al. Breaking solitary waves and breaking wave forces on a vertically mounted slender cylinder over an impermeable sloping seabed[J]. Journal of Ocean Engineering and Marine Energy,2017,3(1):1-19.
[16] Qin X,Motley M R,Marafi N A. Three-dimensional modeling of tsunami forces on coastal communities[J]. Coastal Engineering,2018,140:43-59.
[17] 丁红岩,乐丛欢,刘宪庆,等. 四筒基平台拖航试验分析-水深影响研究[J]. 天津大学学报,2012,45(2):160-166.
Ding Hongyan,Le Conghuan,Liu Xianqing,et al. Towing test of ocean platform with four bucket foundations-impact of water depth[J]. Journal of Tianjin University,2012,45(2):160-166(in Chinese).
Analysis of the Surface Pressure and Force of Piles Under Tidal Bore
Zhang Zhiyong1,Xiao Tingting2,Qi Lan2,Chen Gang1,Zeng Jian1
(1. Key Laboratory of Estuary and Coast of Zhejiang Province,Zhejiang Institute of Hydraulics and Estuary,Hangzhou 310020,China;2. State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300354,China)
The tidal bore is a kind of strong nonlinear discontinuous flow containing large energy.Aiming at the long-term violent impact of pile-type buildings,such as bridge piers,in the Qiantang River estuary area of China under tidal bore,the physical test model is used to test the time-history variation of the surface pressure of piles in the upper and lower parts of the tidal water depth and tidal velocity.The position of the maximum impact pressure of the head is determined and fitted to obtain the formula for calculating the maximum impact pressure.The numerical simulation is used to separate the models of the upper and lower parts of the pile before the tide.The force is separately extracted,analyzed,and fitted to obtain the formula for calculating the tidal force.Results show that the interaction process between the tidal bore and the pile can be divided into three stages.Under the impact of the water depth before the tidal bore,the surface pressure of the pile and the force received will increase instantaneously under the impact of the tide.In terms of the maximum value,the surface pressure and force affected by the water depth before the tide slowly increase.During the attenuated oscillation period,the surface pressure and force received by the pile before the tide rapidly decrease.Moreover,the pressure below the tide depth does not fluctuate.The rate of force attenuation is significantly smaller than that of the pre-tidal water depth.During the flow period,the surface pressure and stress fluctuations of the piles in the upper and lower parts of the tidal water depth gradually decrease.The surface pressure and force under tidal action are negatively correlated with the pre-tidal water depth0and falling tide velocity0and positively correlated with the tidal height.The maximum impact pressure under tidal action occurs near 0.5.The maximum impact pressure and force calculation formula obtained after fitting have good accuracy and can provide a reference for related applications.
tidal bore;pile column;surface pressure;force;empirical formula
TV139.2
A
0493-2137(2020)06-0573-09
10.11784/tdxbz201906012
2019-06-06;
2019-08-27.
张芝永(1984— ),男,博士,高级工程师.
张芝永,zhangzy@zjwater.gov.cn.
国家自然科学基金资助项目(51609214,51609213);浙江省自然科学基金资助项目(LY20E090001).
Supported by the National Natural Science Foundation of China(No.51609214,No.51609213),the Natural Science Foundation of Zhejiang Province,China(No.LY20E090001).
(责任编辑:金顺爱)

