一类轴孔装配混联柔性机构构型综合
宋轶民,郭 振,王攀峰,孙 涛,连宾宾, 2
一类轴孔装配混联柔性机构构型综合
宋轶民1,郭 振1,王攀峰1,孙 涛1,连宾宾1, 2
(1. 天津大学机构理论与装备设计教育部重点实验室,天津 300350;2. 天津大学仁爱学院机械工程系,天津 301636)
被动装配是实现轴孔高精度配合的重要方法之一,其基本原理为柔性装配机构针对外界装配力与装配反力做出自适应柔顺变形,补偿由于工业机器人定位误差导致的轴孔中心线位移偏差及倾角偏差.作为被动装配方法的核心使能部件,柔性装配机构的性能直接决定装配成功与否,为此,开展了一类基于五自由度混联柔性机构轴孔装配的方案设计和柔性机构构型综合研究.该机构由分别具有2T1R(T表述移动运动,R为转动运动)和3R自由度运动的柔性并联模块串联组成,并采用片弹簧作为实现柔顺变形的基本柔性单元.在整体方案设计的基础上,以旋量作为数学工具,提出一种并联柔性机构构型综合的一般流程,讨论在片弹簧不同变形情况下的支链组成形式,拟定支链装配条件.结合实际工况,本文优选出3-RFS-3-RFS作为轴孔装配的柔性机构,利用有限元软件对得到的机构进行仿真以验证机构自由度及各向柔度,仿真结果表明该机构具备五自由度且各向柔性差异小于0.05%. 搭建了轴孔装配实验台,装配实验结果表明对于直径为20mm与10mm的轴孔对,装配成功率分别可达90%与70%.
轴孔装配;构型综合;瞬时旋量;变形控制
轴孔类零件装配是工业生产中常见的作业形式,在汽车、轨道交通、飞行器等领域的机械系统制造装配中均十分重要.自动化装配可极大提高装配效率、缩短机械产品生产周期,已成为轴孔装配主流解决方案[1].依据装配误差调节方式,目前自动化轴孔装配可分为主动装配与被动装配两类[2].其中,主动装配主要依赖于反馈控制伺服环结合精密传感器实现对轴孔零件中心线的高精度定位[3-4].如Zheng等[5]提出了一种基于视觉/力引导和双臂协调轴孔装配策略,根据6轴F/T传感器检测的力和扭矩信息分别实现位置调整和角度调整.被动装配通常在工业机器人与夹持装置之间加入柔顺材料或机构,依靠柔性变形被动补偿由于工业机器人定位产生的位移与角度误差[6].较之主动装配,被动装配不含力反馈执行过程与复杂控制策略,降低了装配系统的运行成本和时间,是自动化轴孔装配的优势方案[1].
柔性机构起源于20世纪80年代末,是指利用材料的弹性变形传递或转换运动、力或能量的一类机构,具有高柔度、轻量化、易加工等特点[7-8].1986年,Whitney[9]率先提出了一种远中心柔顺手腕(RCC),为轴孔被动装配提供了解决方案.然而,早期的RCC装置采用弹簧产生弹性变形,尺寸较大且动态阻尼特性无法满足应用需求[10].为了解决此问题,Lee等[11]提出了可调参数的远中心柔顺机构(VRCC),采用橡胶金属层叠材料(elastomer shear pad,ESP)作为柔性单元,具有柔顺性好、尺寸小、动态阻尼性好等特点,被广泛应用于被动轴孔装配中.但此种装置的问题在于:机构质量较大,降低了轴孔装配的效率和稳定性;机构轴向承载能力较差,无法完成较大轴向力的装配任务[12];虽通过增加限位杆的方式提高了RCC机构的轴向承载能力,但也限制了机构的工作范围[13].
综上,现有轴孔装配机构普遍存在轴向承载能力较差、工作范围较小、侧向柔顺性较弱等缺陷.注意由多条支链共同连接末端动平台的并联机构具有刚度大、承载能力强等特点,有学者提出结合并联机构与柔性材料的并联柔性机构作为自动化轴孔装配的潜在优势解决方案.其首要解决问题为并联柔性机构的结构组成,即构型综合问题.Howell[14]利用刚性机构成熟的理论和方法对柔性机构进行研究,但未扩展至并联柔性机构.Yu等[15]利用旋量理论结合FACT(freedom and constraint topology)方法实现了柔性机构的代数化构型综合,提出了大量并联柔性机构.但此类并联柔性机构主要通过挖槽式的柔性铰链或柔性材料固接于动静平台,虽能实现精准微操作或微调姿,但由于其位移小、变形难以控制,不满足大角度、大位移的调整装配工作要求.
为解决现有并联柔性机构用于轴孔装配存在的问题,本文提出了一种新型并联柔性机构,将柔性单元通过刚性铰链与两端平台连接,由刚性铰链控制柔性单元的变形.另外,为保证较大的柔顺调整范围,采用了混联结构形式串接若干并联柔性机构,形成了一类混联柔性机构.此类机构充分结合了并联机构的轴向高承载能力与调整能力,兼具良好柔顺性,且柔性单元变形可控.其研究难点在于并联柔性机构的构型综合,一是支链的组成形式,需配置不同铰链与柔性单元的连接以控制机构变形;二是支链的布置方式,保证机构具备期望的运动自由度.
本文主要围绕混联柔性机构的构型综合展开,依据轴孔装配的特点提出设计需求,提出了较大范围平稳移动与较小范围精准调姿的混联柔性机构方案;以旋量理论为数学工具,描述基本柔性单元的运动与变形特征,提出了并联柔性机构构型综合的一般流程;分别进行了可实现较大范围内移动与较小范围内调姿的并联柔性机构构型综合,讨论支链的组成形式,结合轴孔装配要求进行构型优选,获得混联柔性机构;并对前述混联柔性机构开展仿真与实验研究,验证了机构自由度与各向柔顺调节的能力,搭建了轴孔装配实验台进行装配实验,实验结果表明本文提出的混联柔性机构可有效提高轴孔装配的成功率.
1 轴孔装配柔性机构方案设计
如图1所示,轴孔被动装配过程可依据轴与孔的相对位置分为接近、调整、入孔3个阶段[16].接近阶段指机构带动轴件运动至孔件中心轴处,受机构定位精度和重复精度所限,轴孔中心轴间存在相对误差.若直接以当前位姿进行轴孔装配,装配阻力过大导致装配失败,甚至可能破坏零件[17].调整阶段是高精度轴孔装配的关键,主要利用柔性机构调整轴与孔的相对位姿,减少轴孔的位移和角度偏差.在入孔阶段,柔性机构需克服孔壁摩擦阻力,使待装配轴稳定运动,避免产生振动而加大装配误差.依据上述轴孔装配过程,柔性机构应满足如下设计要求:
(1) 具备较大轴向承载能力,以承载轴孔装配时的摩擦反力;
(2) 具备位置与角度调整能力;
(3) 具备各向同性柔度,保证机构柔度差异小.
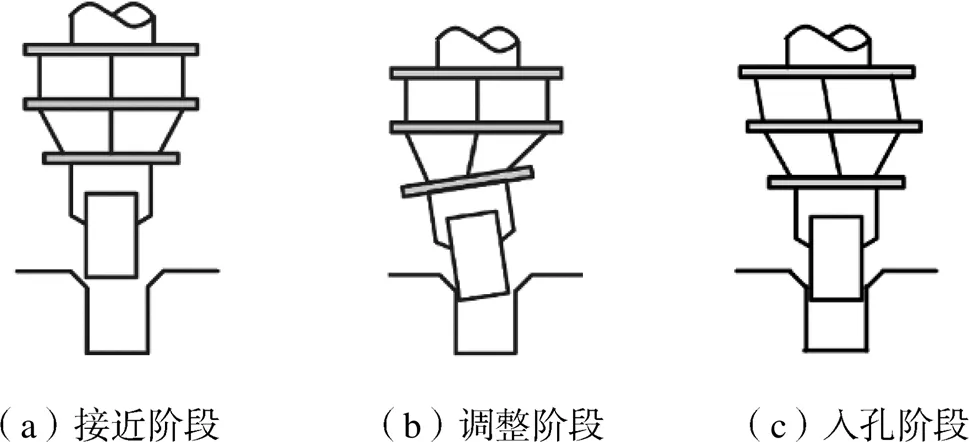
图1 轴孔装配的3个阶段
依据轴孔装配的设计需求,为保证柔性机构具有较大承载能力,拟采用并联机构形式将多个柔性支链连接动平台.柔性机构需具备调节空间倾角及偏置轴线位置的能力,因此需保证机构具有2T3R(两转动三平动)自由度.为保证较大的柔顺调整范围,拟采用混联机构形式,即柔性机构分为较大范围移动的柔性并联模块与较小范围调姿的柔性并联模块.柔性并联模块应具有2T1R自由度,柔性并联模块应具有3R自由度,两个柔性并联模块串接形成了混联柔性机构.此混联柔性机构可作为末端执行器与工业机器人连接组成轴孔装配的完整执行系统,如图2所示.
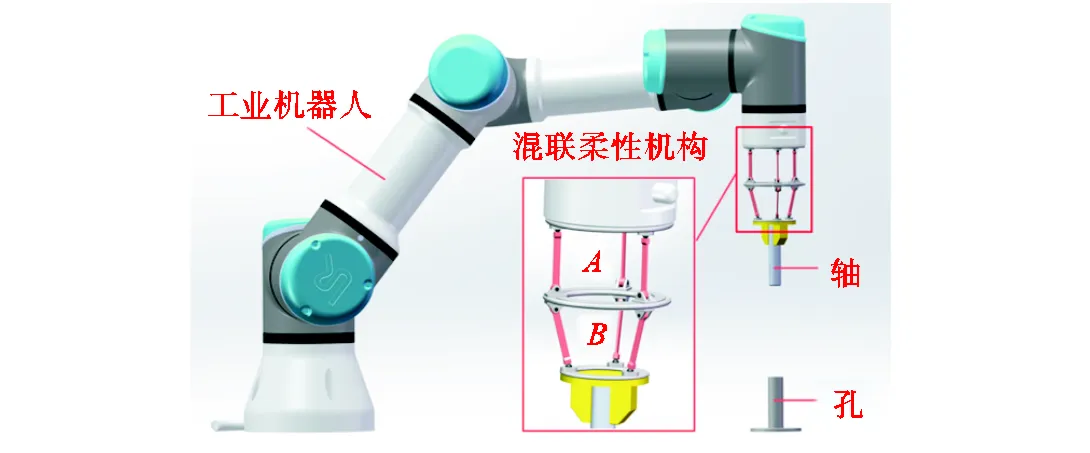
图2 基于混联柔性机构的轴孔装配方案
2 混联柔性机构构型综合方法
2.1 旋量理论
本文以旋量理论[18-20]为数学工具开展并联柔性机构的构型综合方法研究.首先简要介绍旋量理论的基本数学原理.
依据Chalse定理,空间内任一刚体的运动可视为螺旋运动,即一般运动可等效为绕着运动轴线的转动与沿着运动轴线的移动.在物体运动的某一瞬间,其瞬时螺旋轴可表示为
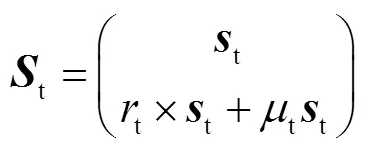
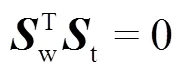
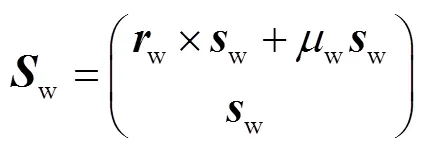
2.2 基本柔性单元
基本柔性单元直接决定了并联柔性机构的柔顺调整能力.常见的柔性单元有缺口型铰链、柔性杆、螺旋弹簧、片弹簧、卷簧、柔性软管等.其中,缺口型铰链的变形范围有限,且缺口处容易疲劳受损,无法承受轴向载荷.卷簧的变形能力有限,自由度少,螺旋弹簧与柔性软管轴向承载不稳定.因此适用于混联柔性机构的柔性单元有柔性杆与片弹簧两类.实际情况是,柔性杆与片弹簧也是以往传统并联柔性机构中应用最多的两种柔性单元,相比柔性杆的变形方向难以预测,片弹簧的变形方向更加受控制.综上,本文拟选用片弹簧作为基本柔性单元,原因如下:①无应力集中现象;②元件的各处都产生了变形,材料性能得以充分发挥;③自由度多,具备一定的轴向承载能力;④变形易于控制.基于上述原因,本文采用片弹簧作为混联柔性机构的基本柔性单元.不失一般性,片弹簧的坐标系如图3所示.
由图3可知,片弹簧最多可产生3处变形:2个平行于方向的弯曲变形与1个方向的扭转变形.此时,片弹簧可记为F(Ry, Ry, Rz),下标R、R和R表示片弹簧方向的弯曲变形和方向的扭转变形.根据片弹簧的变形特点,可将其抽象为3个转动副,等效转动副的运动螺旋可表示为
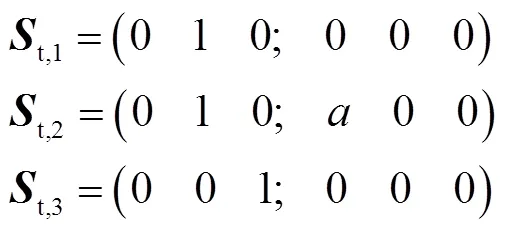
利用式(2)可求得片弹簧的约束旋量为
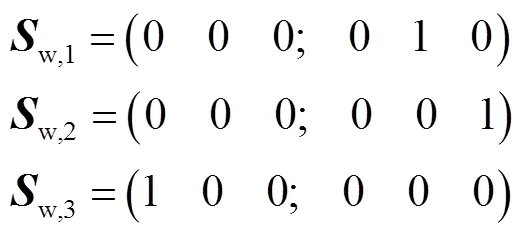
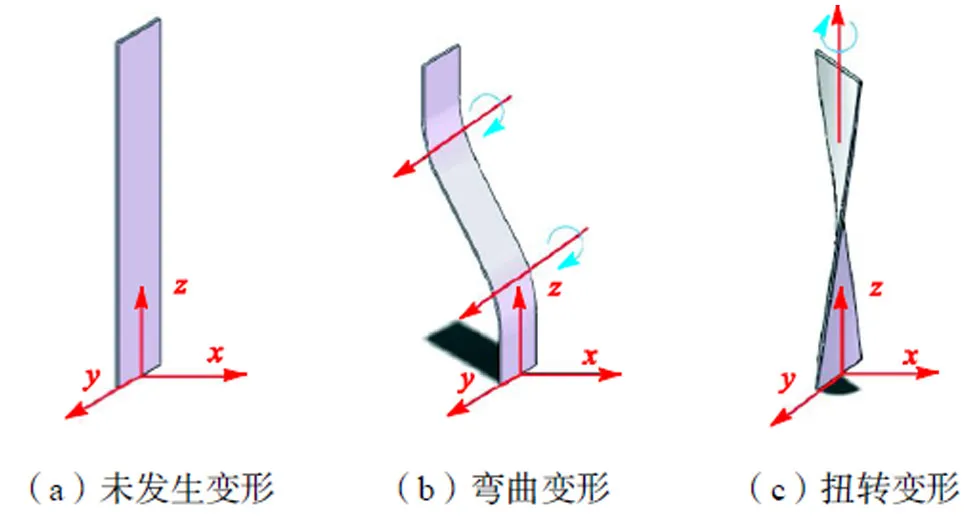
图3 片弹簧变形
2.3 混联柔性机构构型综合一般流程
以旋量理论作为数学工具,本文提出了一类带有铰链的混联柔性机构构型综合的方法,其基本流程如图4所示.
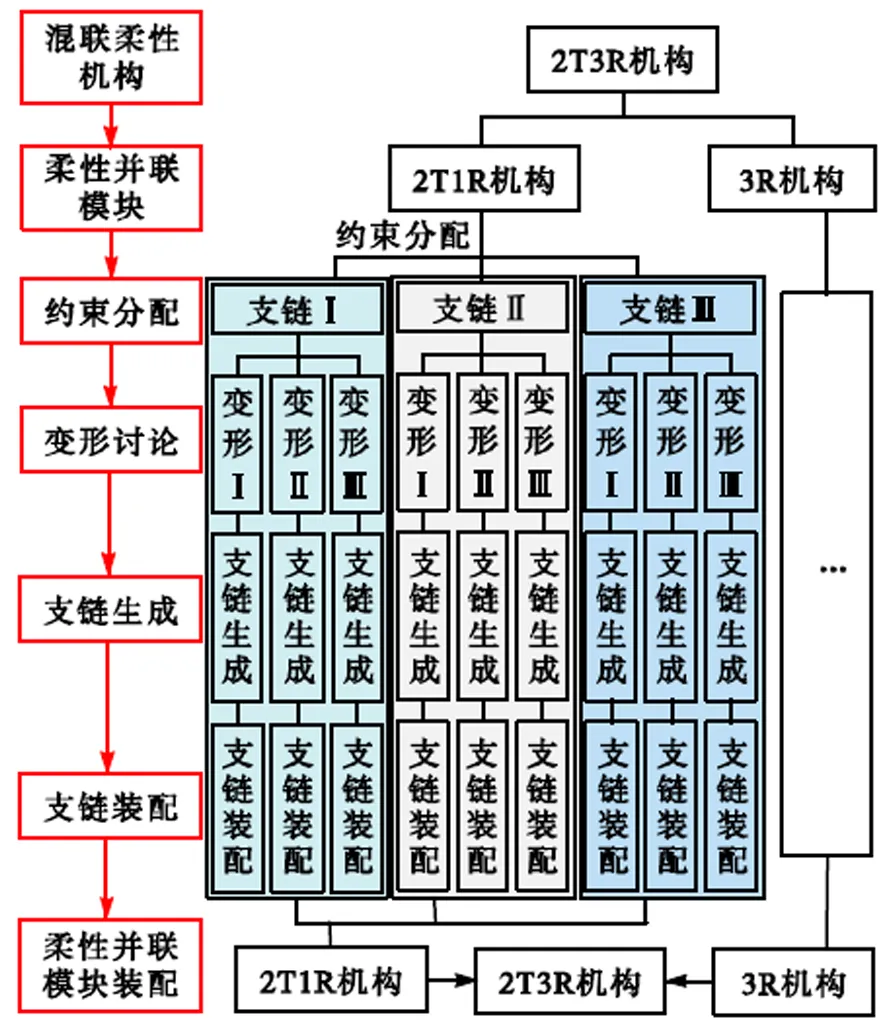
图4 基于旋量理论的混联柔性机构构型综合流程
3 2T1R并联柔性模块构型综合
首先进行2T1R并联柔性机构的设计.该柔性并联模块末端的运动螺旋可描述为
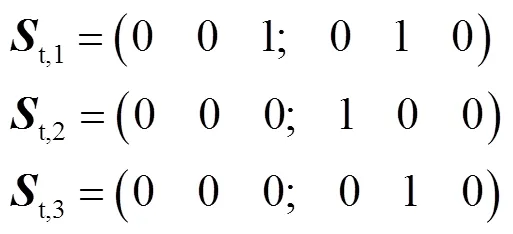
由式(2)可得其末端的约束螺旋为
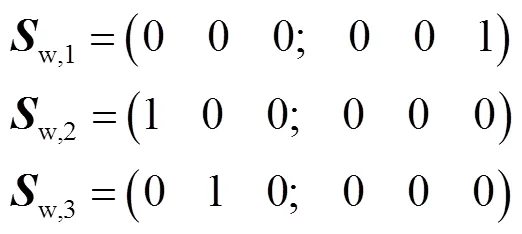
该螺旋系由3个线性无关的约束螺旋组成,表征动平台受到方向的力约束和、方向的力偶约束.由力的线性叠加性质,可获得机构动平台的等效约束形式[19].
由式(5)及约束力分配原理,按照每条支链提供的约束数目,1T2R柔性并联模块组成支链的约束力组合形式如表1所示(以3条支链为例).
表1 支链约束力组合形式
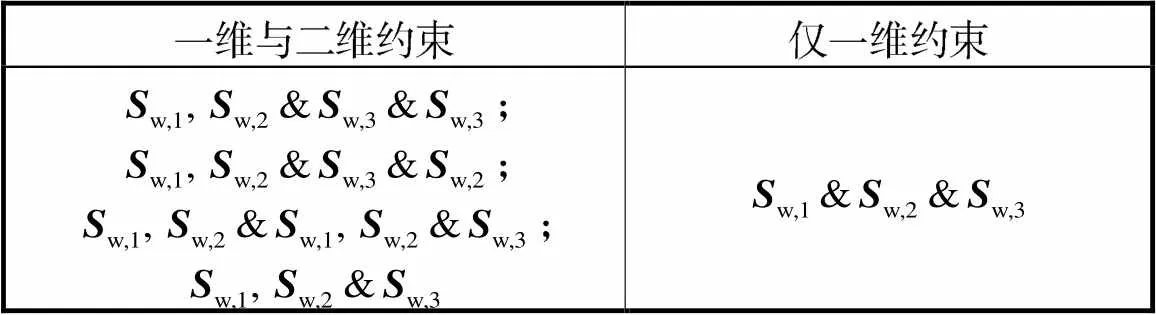
Tab.1 Constraint combination form of limbs
由于片弹簧自身最少可提供两个力和一个力偶约束,限制了末端动平台的移动运动需求,因此需通过增加运动副的形式消除一个约束力.由于六自由度支链需额外配置恰约束运动支链,在机构综合中不加以考虑.按照自由度数目,支链可分为四自由度和五自由度支链.
由式(4)可知片弹簧最多产生3处变形,而发生不同形式的变形会影响支链的刚性及耐久性.因此下面分别讨论片弹簧在不同变形情况下四自由度和五自由度柔性组成支链的拓扑形式.
3.1 四自由度柔性支链综合
通过前述分析可知,柔性组成支链可提供一个力和力偶约束为
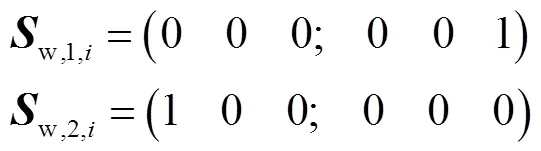
此时其运动螺旋可求解为
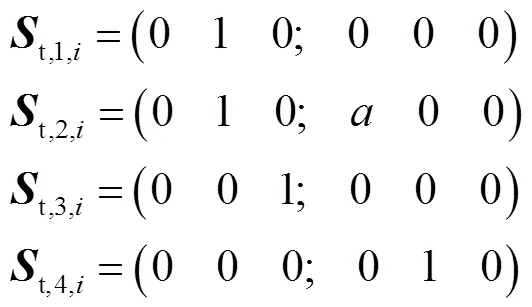
因此该类柔性支链具有2R2T四自由度,可描述为PPRR.
1)情况1:片弹簧产生3处变形
2)情况2:片弹簧产生两处变形
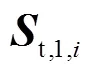
3)情况3:片弹簧产生一处变形
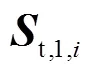
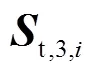
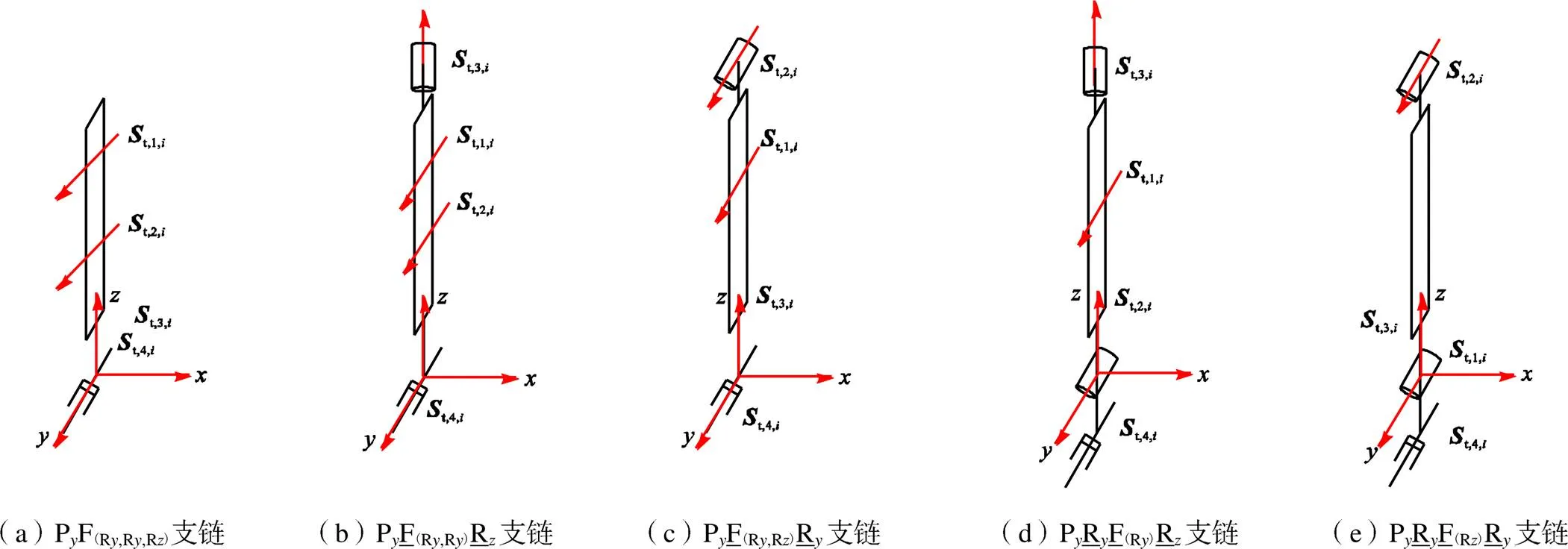
图5 2R2T四自由度柔性支链
综上,利用旋量理论约束综合法,共获得24种四自由度柔性支链,如表2所示.构成的柔性支链均提供片弹簧长边方向的约束力和垂直平面方向的约束力偶.
表2 四自由度柔性支链
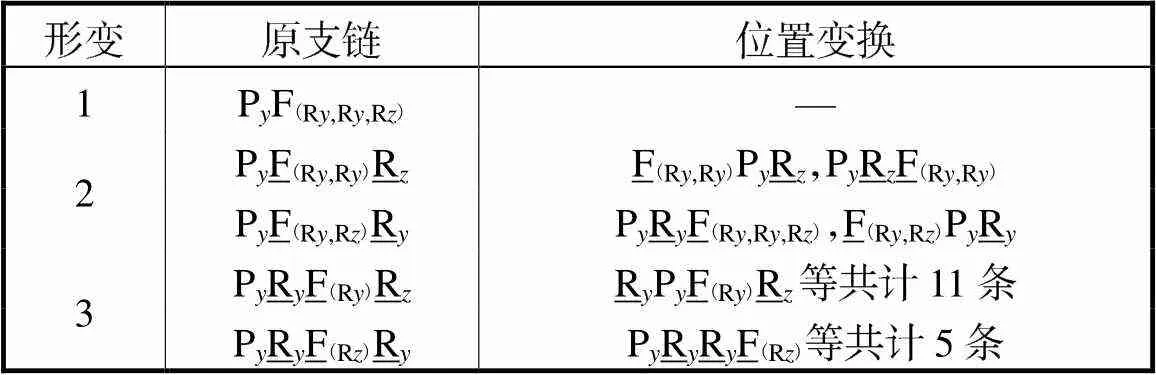
Tab.2 Flexible limbs with four degrees of freedom
3.2 五自由度柔性支链综合
五自由度柔性支链可提供一个约束力或一个约束力偶.
当支链提供一个力约束,力螺旋表示为
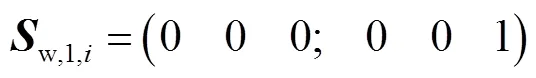
此时支链运动螺旋为
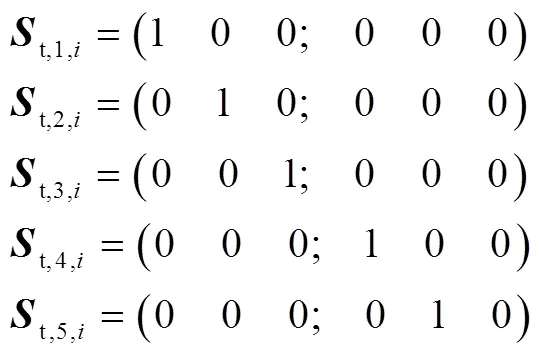
该类柔性支链具有3R2T五自由度,可描述为RRRPP.
当支链提供一个力偶约束,力偶螺旋为
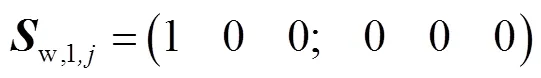
此时支链运动螺旋为
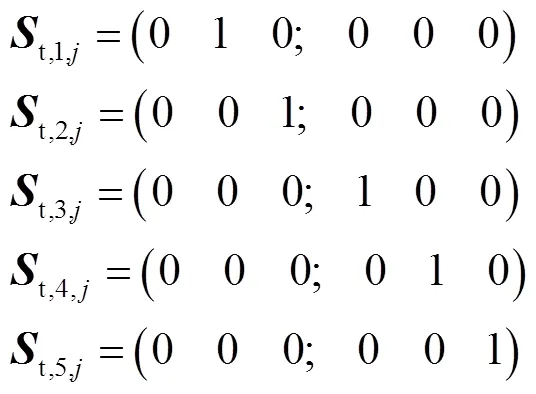
该类支链具有2R3T五自由度,可描述为RRPPP.
1)情况1:片弹簧产生3处变形
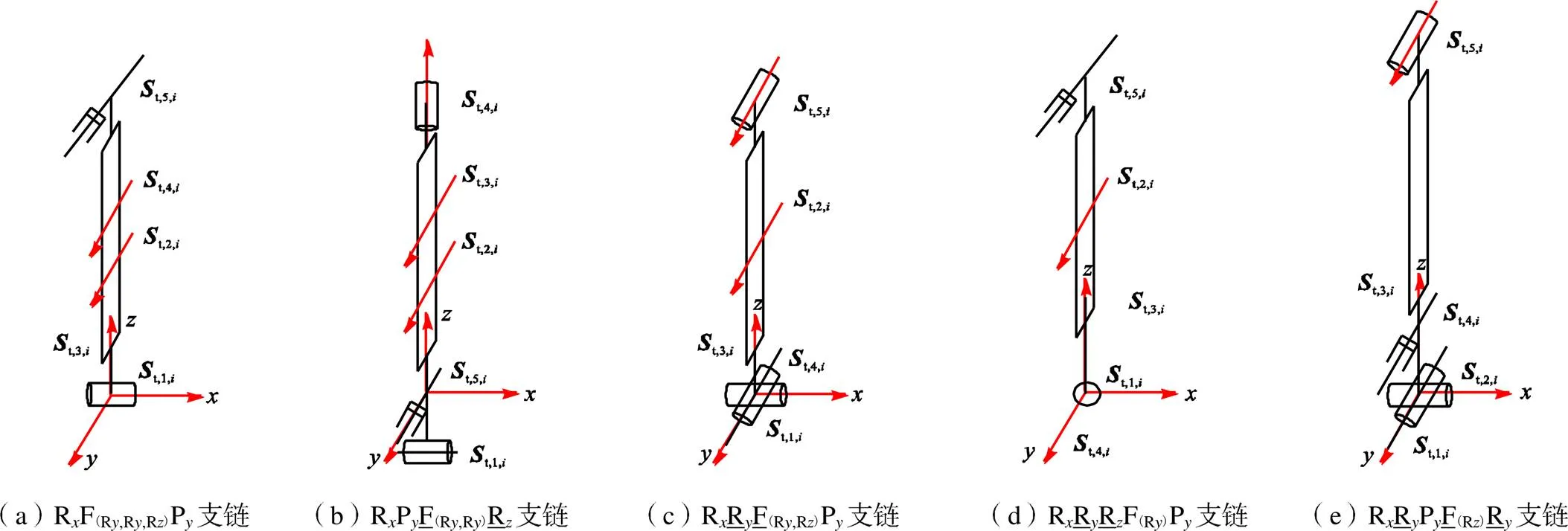
图6 2T3R五自由度柔性支链
2)情况2:片弹簧产生两处变形
(1) 片弹簧沿短边发生两处弯曲变形.
(2) 片弹簧发生沿短边发生一处弯曲变形且沿长边发生扭转变形.
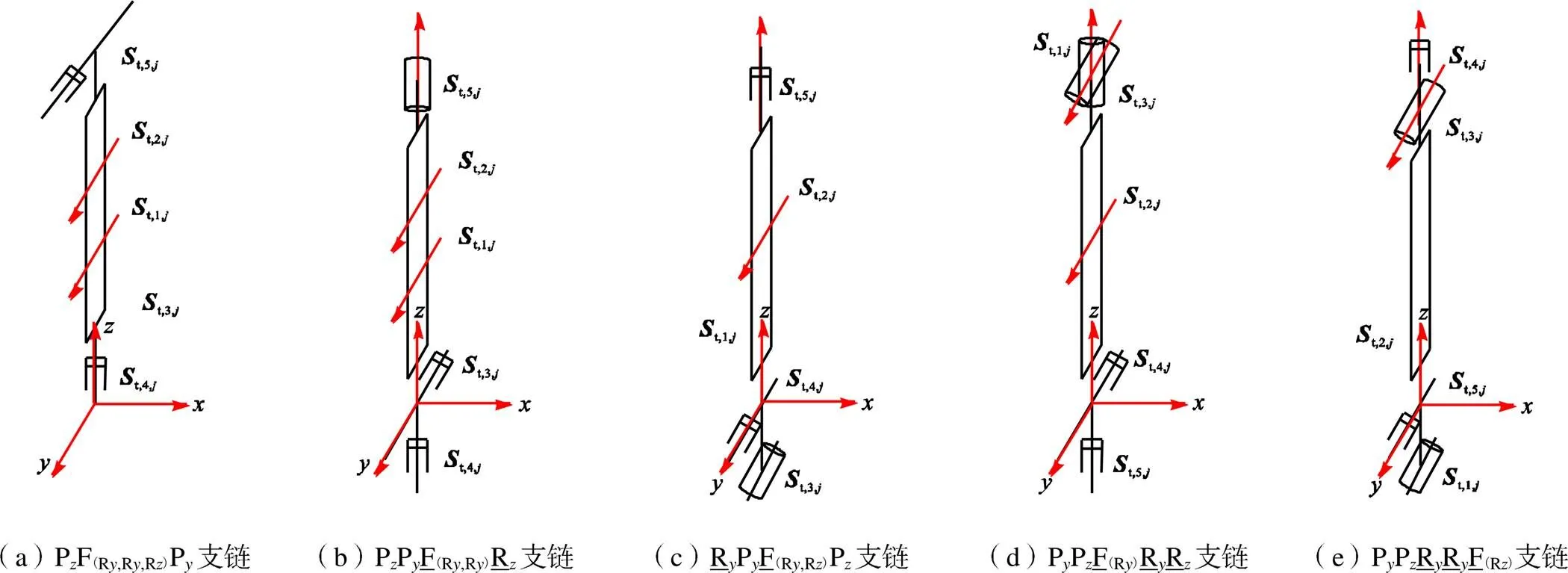
图7 3T2R五自由度柔性支链
3)情况3:片弹簧产生一处变形
(1)片弹簧沿短边发生弯曲变形.
(2)片弹簧沿长边发生扭转变形.
综上,利用旋量理论约束综合法,如表3所示,共获得176类2T3R柔性组成支链,构成的柔性支链均提供片弹簧长边方向的约束力;共获得117类3T2R柔性组成支链,构成的柔性支链均提供片弹簧垂直平面方向的约束力偶.
表3 五自由度柔性支链
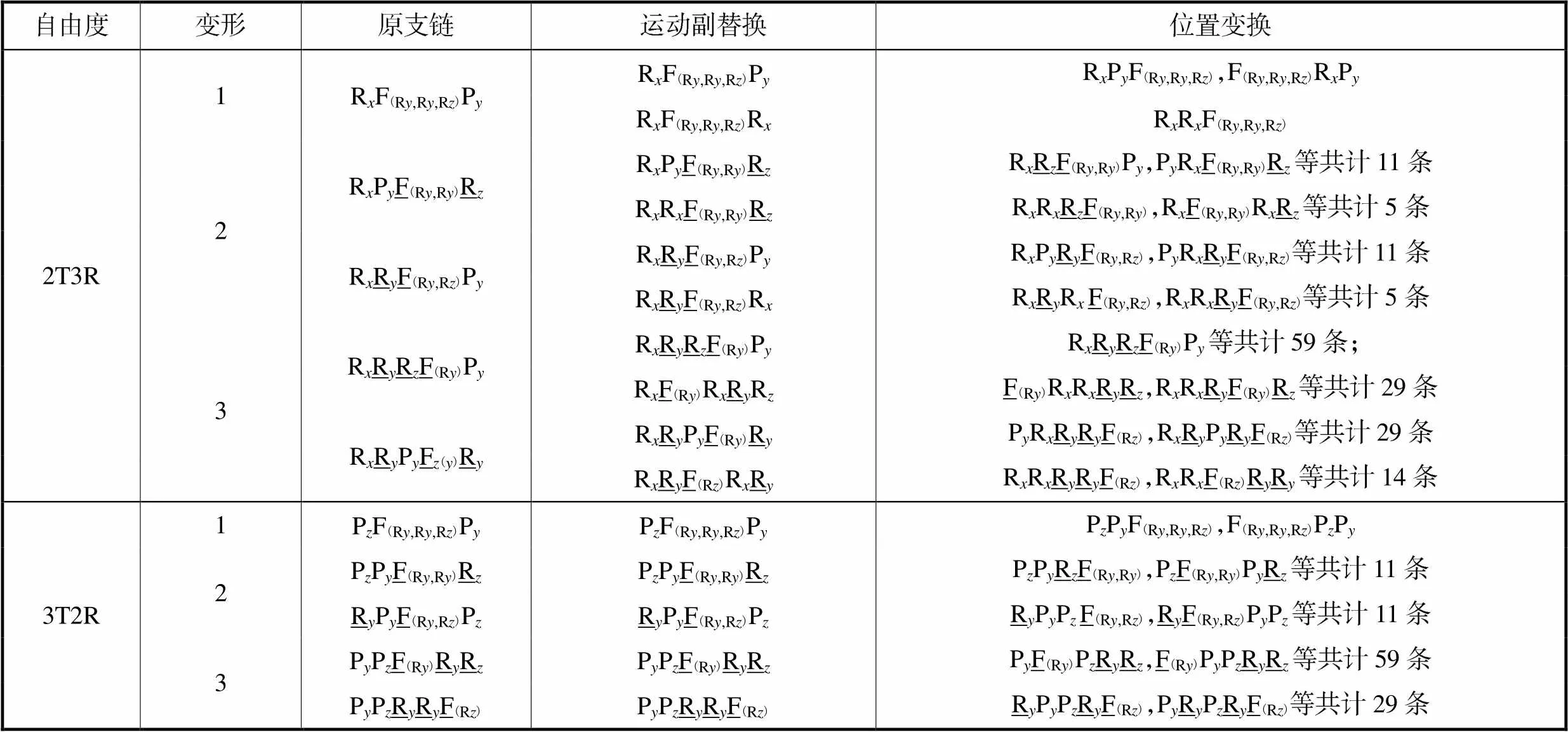
Tab.3 Flexible limbs with five degrees of freedom
3.3 装配条件
获得柔性支链后,需选择支链装配形成2T1R柔性并联模块.支链的选取和装配应满足表1所示约束力分配形式.另外,为保证机构具有期望运动,还需满足以下条件:
(1) 支链片弹簧长边方向在空间内均应平行且不共面;
(2) 任意选取3条2T3R柔性支链,满足装配条件(1)均可构成2T1R柔性机构.
根据上述装配条件进行支链装配可获得一系列2T1R柔性并联模块.以R(Ry,Rz)R(UFR)、R(Rz)R(UFU)、R(Ry)R(RFS)为例进行装配,见图8.
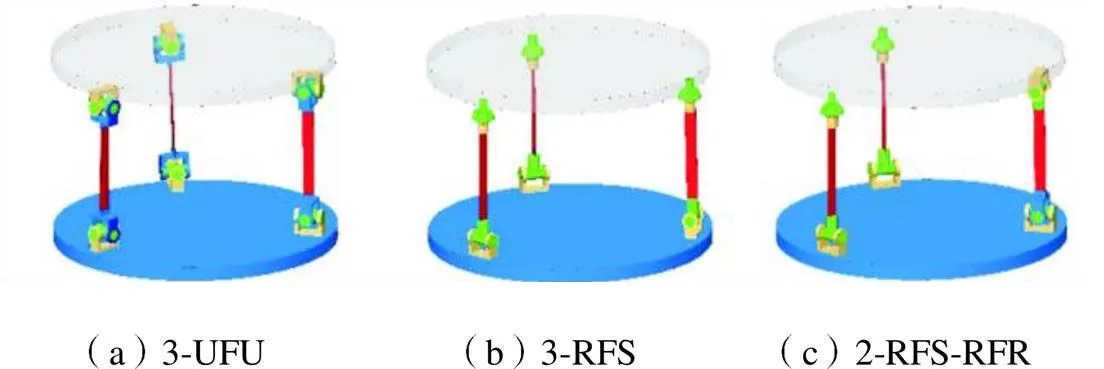
图8 2T1R柔性并联模块
根据设计要求可知,3条支链的形式应尽可能相同;片弹簧尽量只发生方向的弯曲变形,保证支链柔性高且不易损坏.综上分析,满足条件的并联柔性机构为3-RF(Ry)S,见图9.给定动平台任意方向的位移,经检查动平台所受约束螺旋系未发生变化,该机构满足全周期自由度要求.

图9 2T1R柔性并联模块(3-RF(Ry)S)
4 3R并联柔性模块构型综合
该柔性并联模块末端的运动螺旋可描述为
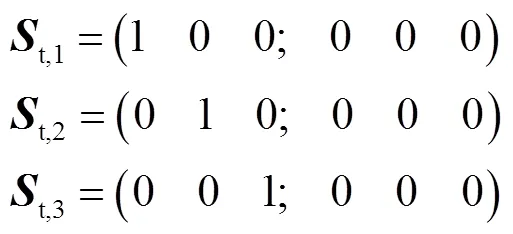
由式(2)可得其末端的约束螺旋为

该螺旋系由3条线性无关量组成,表征动平台受到、、方向的力约束,等效于空间内3个交于一点的力约束.
通过前述分析可知,3R柔性并联模块的支链应具备3R1T或3R2T自由度,后者的综合结果见表3.针对3R1T柔性支链,其约束螺旋可描述为
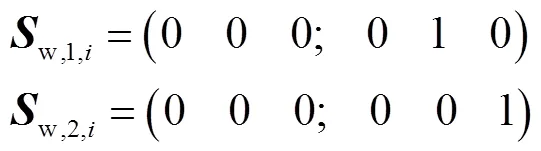
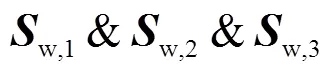
同理,3R2T支链的选取和装配需满足的装配原则为:任意选取3条3R2T柔性支链,片弹簧长边方向在空间内轴线交于一点且不共面装配均可构成3R柔性机构.
由第3.3节可知,3-RFS支链具备较好的变形特性,适用于轴孔装配.因此本节同样选取3-RF(Ry)S支链作为3R机构的支链,如图10所示.对给定动平台任意方向的位移,经检查动平台所受约束螺旋系未发生变化,该机构满足全周期自由度要求.
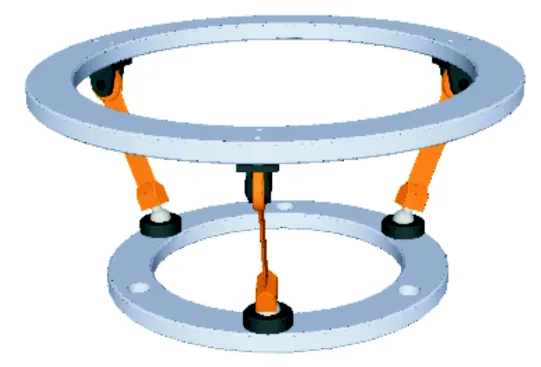
图10 3R柔性并联模块(3-RF(Ry)S)
将第3.3节得到的2T1R并联柔性模块与本节得到的3R并联柔性模块进行串联组装,最终获得混联柔性机构,如图11所示.
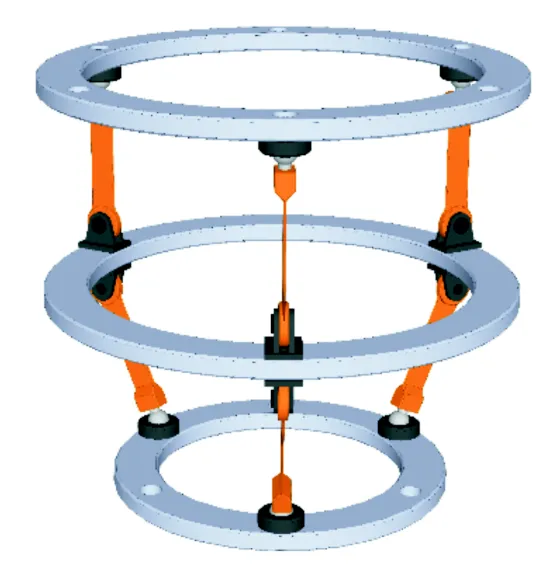
图11 混联柔性机构
5 仿真与实验验证
利用有限元分析可以准确地反映柔性单元与外部载荷的非线性关系.本文利用ABAQUS有限元软件对第4节得到的混联柔性机构进行仿真,验证机构自由度及各向柔度.
首先建立机构的有限元模型,动、静平台采用45号钢,具有不易变形、强度高等特点.片弹簧采用硅锰弹簧钢(60Si2Mn),具有强度大、弹性高等特点. 仿真材料参数见表4.
表4 仿真材料参数

Tab.4 Material parameters of the simulation
其次对机构模型进行简化,去除圆角、倒角等工艺特征的影响,简化后的模型如图12所示.
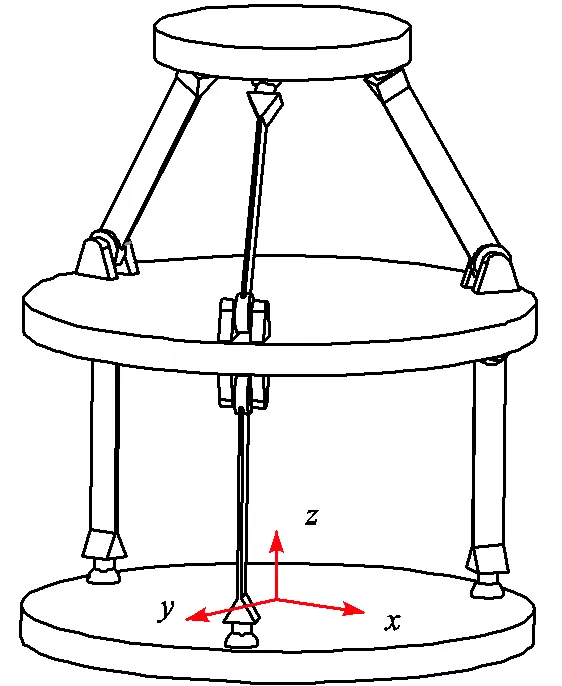
图12 用于仿真的混联柔性机构
针对上述机构进行运动自由度的仿真验证,仿真结果如图13所示,证明机构具备2T3R五个自由度.

图13 自由度仿真结果
针对柔性机构进行静力学分析.固定下平台,分别沿与轴呈0°~60°方向(间隔5°)对上平台施加单位力和单位力矩,选取其中3个方向的变形,如图14~16所示.从不同方向施加单位载荷时,各向位移差异小于0.05%,从不同方向施加力矩时,角度变化相同,表明机构具有较好的各向同性柔度.
为了验证所述混联柔性机构满足轴孔装配要求,本文搭建了轴孔装配实验台,如图17所示.
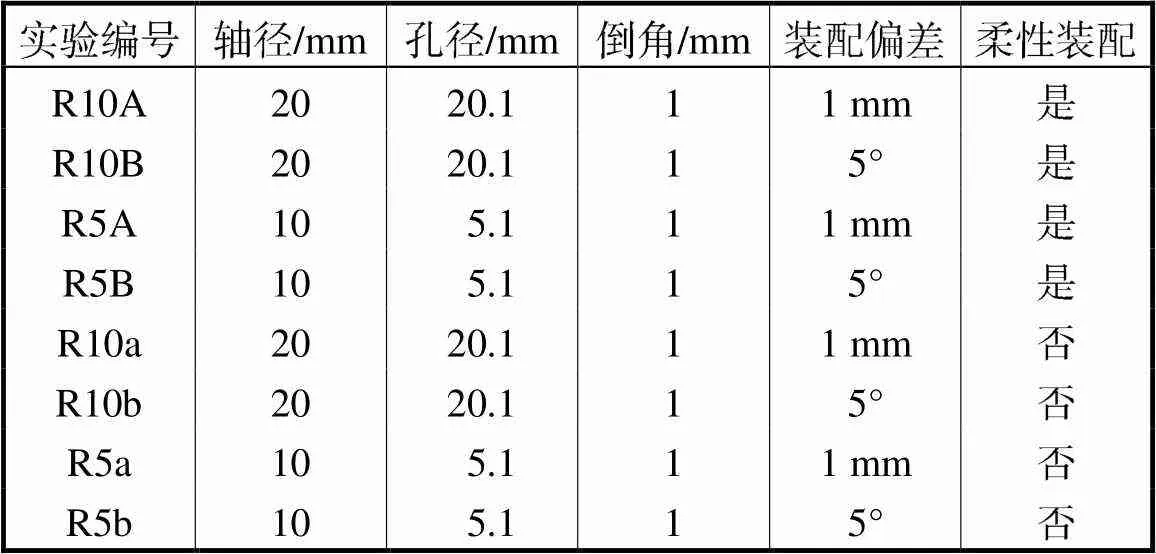
利用上述实验台本文设计了8组实验,见表5.
针对R10和R5两组轴孔对,使工业机器人产生1mm和5°的轴线偏差,检验混联柔性机构的位移与角度调整能力.轴孔实验分别以A(a)、B(b)表示.同时,设置了4组不含柔性机构的对照组R10a、R10b、R5a、R5b,分别与含有柔性机构的实验组R10A、R10B、R5A、R5B进行对照(图18).
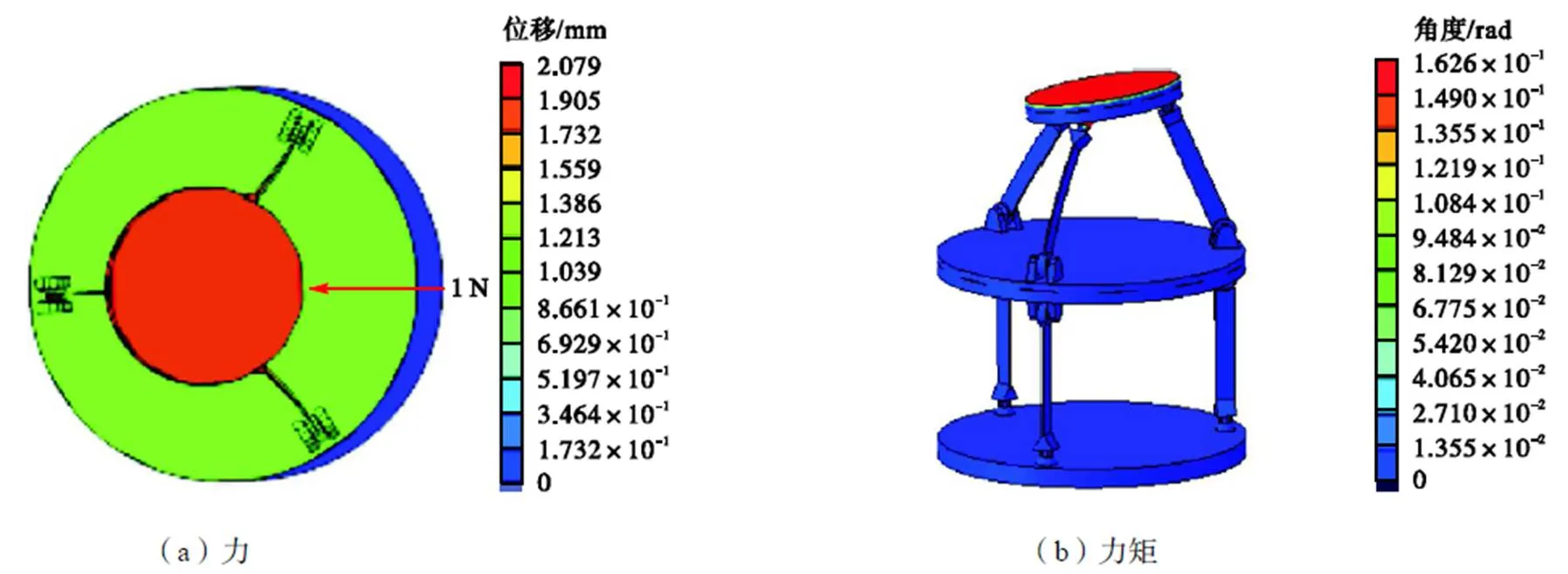
图14 沿x轴的力与绕x轴的力矩

图15 与x轴呈30°的力与绕此方向的力矩
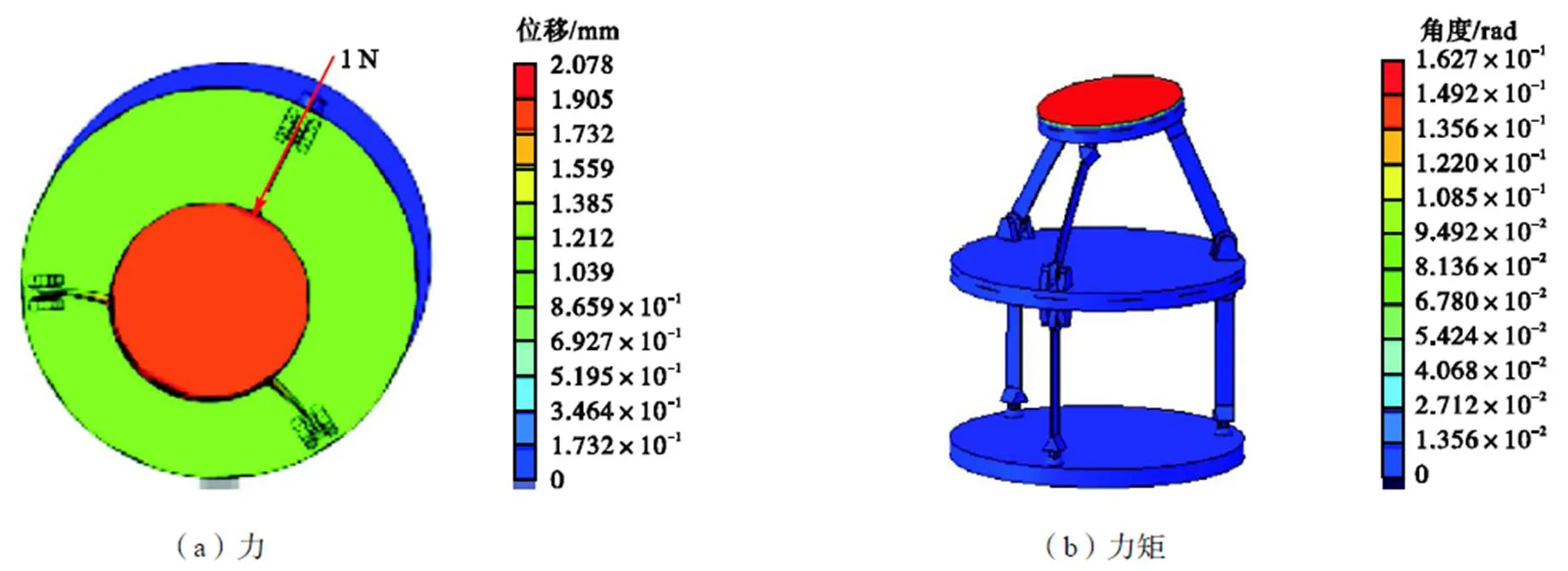
图16 与x轴呈60°的力与绕此方向的力矩
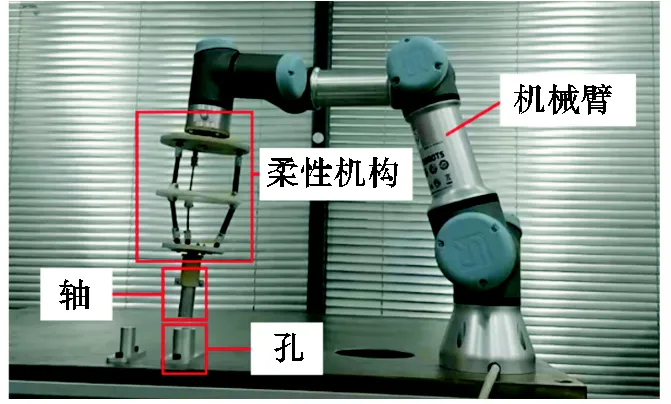
图17 轴孔装配实验台
实验时,工业机器人夹持轴件从孔件上方1cm处开始慢慢接近孔件,随后混联柔性机构开始调姿,直至装配完成.装配过程(以R10B为例)见图19,对上述8类实验分别进行5次轴孔装配实验,观察装配完成情况以及并混联柔性机构调姿情况,装配结果见表6.
表5 轴孔装配实验编号
Tab.5 Serial numbers of the peg-in-hole assembly

图18 对照实验
表6中“√”表示装配成功,“×”表示装配失败.由表6可知,通过与对照实验对比发现,本文综合的并混联柔性机构可有效的完成轴孔装配过程.对于直径20mm及10mm的轴孔对,装配成功率可达90%与70%.另外,对比R10A与R5A,R10B与R5B发现,随着轴孔对直径的减小,轴孔装配的难度随之提高.
表6 轴孔装配实验结果

Tab.6 Experiment results of the peg-in-hole assembly
6 结 论
结合轴孔装配的实际需求,本文提出一类混联柔性机构的被动装配方案,开展了其构型综合研究与仿真实验验证,得到结论如下.
(1) 本文提出了一种混联柔性机构的构型综合一般流程.分别针对2T1R与3R并联柔性模块进行构型综合,得到了满足轴孔装配条件的混联柔性机构.
(2) 利用有限元软件对混联柔性机构进行了自由度与柔度仿真,结果显示本文提出的机构自由度符合装配要求,各向柔度差异小于0.05%.
(3) 搭建了轴孔装配实验台,并对混联柔性机构的装配性能进行了验证.结果表明,该机构可有效地提高装配成功率,对于直径20mm和10mm的轴孔对成功率分别为90%与70%.
[1] Park H,Park J,Lee D H,et al. Compliance-based robotic peg-in-hole assembly strategy without force feedback[J]. IEEE Transactions on Industrial Electronics,2017,99:6299-6309.
[2] Haskiya W,Qiao H,Knight J A G. A new strategy for chamferless peg-hole assembly[C]//IEEE International Symposium on Assembly and Task Planning. England,UK,1997:90-95.
[3] Xu Yin,Hu Yue,Hu Lei. Precision peg-in-hole assembly strategy using force-guided robot[C]//Proceedings of the 3rd International Conference on Machinery,Materials and Information Technology Applications. Changsha,China,2014:1406-1412.
[4] Kim Y L,Kim B S,Song J B. Hole detection algorithm for square peg-in-hole using force-based shape recognition[C]// IEEE International Conference on Automation Science and Engineering(CASE). Seoul,Korea,2012:1074-1079.
[5] Zheng Yanglong,Zhang Xianmin,Chen Yanlin,et al. Peg-in-hole assembly based on hybrid vision/force guidance and dual-arm coordination[C]//2017 IEEE International Conference on Robotics and Biomimetics(ROBIO). Macau,China,2017:418-423.
[6] 欧阳帆,张 铁,陈 杨. 用于机器人轴孔装配的主-被动结合柔顺装置[J]. 华南理工大学学报:自然版,2016,44(7):61-68.
Ouyang Fan,Zhang Tie,Chen Yang. Active-passive compliant device for peg in hole assembly[J]. Journal of South China University of Technology:Natural Science Edition,2016,44(7):61-68(in Chinese).
[7] 于靖军,郝广波,陈贵敏,等. 柔性机构及其应用研究进展[J]. 机械工程学报,2015,51(13):53-68.
Yu Jingjun,Hao Guangbo,Chen Guimin,et al. Research progress on flexible mechanisms and their applications[J]. Journal of Mechanical Engineering,2015,51(13):53-68(in Chinese).
[8] Nishiwaki S,Frecker M I,Min S,et al. Topology optimization of compliant mechanisms using the homogenization method[J]. International Journal for Numerical Methods in Engineering,2015,42(3):535-559(in Chinese).
[9] Whitney D E. Remote center compliance[J]. Encycl Robot Control,1986,104:1316-1324.
[10] 王四平. 具有柔顺手腕的四自由度装配机器人的设计与研究[D]. 哈尔滨:哈尔滨工业大学,2008.
Wang Siping. Design and Research of 4 DOF Assembly Robot with Pliant Wrist[D]. Harbin:Harbin Institute of Technology,2008(in Chinese).
[11] Lee S,Won S,Choi S. Development of a new variable remote center compliance for assembly robots[J]. Advanced Robotics,2000,14(1):241-255.
[12] 宋美江. 复合型柔性腕的开发设计及产品化研究[D]. 天津:天津大学机械工程学院,2004.
Song Meijiang. Development,Design and Productization of Composite Flexible Wrist[D]. Tianjin:School of Mechanical and Engineering,Tianjin University,2004(in Chinese)
[13] 戚江波,何 薇,肖军娜. 一种被动柔顺装置:CN201720253028. 5[P]. 2017.
Qi Jiangbo,He Wei,Xiao Junna. Passive Compliant Device:CN201720253028.5[P]. 2017(in Chinese).
[14] Howell L L. Compliant Mechanisms[M]. New York:John Wley & Sons Inc,2001.
[15] Yu Jingjun,Li Shouzhong,Su Haijun,et al. Screw theory based methodology for the deterministic type synthesis of flexure mechanisms[J]. Journal of Mechanism and Robotics,2011,3(3):031008.
[16] Southern W R,Lyons C G. The study of a passive accommodation device in robotic insertion processes[J]. Journal of Materials Processing Technology,2002,124(3):261-266.
[17] Du Kelin,Zhang Biaobiao. Dynamic analysis of assembly process with passive compliance for robot manipulators[C]//IEEE International Symposium on Computational Intelligence in Robotics & Automation. Kobe,Japan,2003:1168-1173.
[18] Zhao Jingshan,Feng Zhijing,Dong Jingxin. Computation of the configuration degree of freedom of a spatial parallel mechanism by using reciprocal screw theory[J]. Mechanism & Machine Theory,2006,41(12):1486-1504.
[19] Mustafa S K,Agrawal S K. On the force-closure analysis of-DOF cable-driven open chains based on reciprocal screw theory[J]. IEEE Transactions on Robotics,2012,28(1):22-31.
[20] Fang Hairong,Fang Yuefa,Zhang Ketao. Reciprocal screw theory based singularity analysis of a novel 3-DOF parallel manipulator[J]. Chinese Journal of Mechanical Engineering,2012,25(4):647-653.
Type Synthesis of Hybrid Compliant Mechanisms for Peg-in-Hole Assembly
Song Yimin1,Guo Zhen1,Wang Panfeng1,Sun Tao1,Lian Binbin1, 2
(1. Key Laboratory of Mechanism Theory and Equipment Design of Ministry of Education,Tianjin University,Tianjin 300350,China;2. Department of Mechanical Engineering,Tianjin University Ren’ai College,Tianjin 301636,China)
Passive assembly is an important method in peg-in-hole assembly.The assembly and reaction forces result in adaptive deformation of the compliant mechanism,which depends on the deformation to compensate for the position and angular deviations.As the key point of a passive assembly device,the performance of compliant mechanisms determines whether the assembly is successful or not. Therefore,a kind of hybrid compliant wrist with five degrees of freedom,which is composed of two parallel compliant modules with 2T1R(T and R denote translational and rotational motions,respectively)and 3R mobility,was proposed and designed in this study.First,a novel passive assembly device was proposed.Then,using screw as a mathematical tool,a general process for configuration synthesis of parallel complaint mechanisms is proposed.Available limbs were generated on the basis of the deformation conditions of the plate spring and the assembly principles.Finally,the 3-RFS-3-RFS hybrid compliant mechanism was selected for the peg-in-hole assembly.The finite element simulation showed that the hybrid compliant mechanism can adjust the displacement and angle errors well.Moreover,flexibility in all directions is changeable by no more than 0.05% and with no difference in all angles.A peg-in-hole assembly test bench was built.The assembly test results show that the assembly success rate can reach 90% and 80% for peg and hole pairs with diameters of 20 and 10mm,respectively.
peg-in-hole assembly;type synthesis;instantaneacs screw;deformation control
TH122
A
0493-2137(2020)06-0582-11
10.11784/tdxbz201906034
2019-06-17;
2019-09-07.
宋轶民(1971— ),男,博士,教授,ymsong@tju.edu.cn.
王攀峰,panfengwang@tju.edu.cn.
国家自然科学基金资助项目(51875391,51875392);天津市新一代人工智能科技重大专项资助项目(18ZXZNGX00350);天津市自然科学基金京津冀专项资助项目(17JCZDJC40400).
Supported by the National Natural Science Foundation of China(No.51875391,No.51875392),Tianjin New Generation Artificial Intelligence Technology Major Project(No.18ZXZNGX00350),Tianjin Natural Science Foundation Beijing-Tianjin-Hebei Special Project(No.17JCZDJC40400).
(责任编辑:孙立华)

