基于模型参考自适应的大气层外杀伤拦截器姿态控制系统设计 ①

仲 秦，闫 杰，张晓峰，武文斌

(1.西北工业大学 航天学院，西安 710072；2.西北工业大学 无人系统技术研究院，西安 710072； 3.西安现代控制技术研究所，西安 710065)

0 引言

EKV姿态控制系统在拦截器飞行的不同阶段承担不同的任务。姿态控制系统的精度和指标直接影响到拦截器的总体性能。在中制导段校正时，姿态控制系统的任务就是控制弹体纵轴的方向和中制导需求推力的方向垂直，同时保证弹体的姿态角速度稳定。在中制导段完成时，又要求弹体的纵轴对准目标的方向以便拦截器的红外探测器可以捕获目标。当拦截器进入末制导自动寻的阶段后，在捕获目标之后，姿态控制的主要任务则是令探测器能够稳定地跟踪目标，即将目标始终保持在视场范围之内。拦截器的姿态可能需要作大角度调整，而且要求快速性。因此，对于拦截器的姿态控制系统来说，其控制精度和快速性直接影响到制导系统的性能，并对拦截器的最终拦截精度产生明显的影响。姿态控制在两个阶段要求姿态控制系统能够跟踪一定的角度，并且具有很好的快速性。

欧洲防务集团的Stéphanie Joner介绍了大气层外动能拦截系统EXOGUARD的GNC方案，拦截器采用4个固体燃料轨控发动机以及6个固体燃料姿控发动机的配置[1]。Andrieu V介绍了一种基于输出反馈的制导控制一体化方法，用以拦截大气层外不带机动的目标[2]。谷良贤分别建立了轨控和姿控发动机模型，并通过角度和角速度的稳定设计了开关控制器[3]。杨宝庆基于模型预测控制进行拦截器姿态控制设计，并通过采用约束“紧缩”的方法，求解优化问题，达到鲁棒性要求[4]。刘世勇与魏明英采用一种切换控制方法，给出了双重推力水平切换控制逻辑、像平面控制与准滑模控制切换准则、角度反馈控制切换策略，仿真表明所设计的系统可以适应大气层内外飞行，鲁棒性较强[5-6]。刘孝马根据视线角偏差设计了姿态控制率，并设计了喷管门限值进行死区限制，避免了频繁的开关[7]。刘凯针对导弹的喷管发动机直接力控制问题，引入了模糊逻辑的方法，有效减少了系统的抖振[8]。史鲲将直气复合拦截弹的内动态进行了快慢回路划分，并分别设计了控制器，并利用动态分配技术，将计算得到的连续控制指令分配到舵系统与直接力系统[9]。张宇针对大气层外拦截器设计了基于滑模变结构方法的姿态控制器，同时为解决变结构方法的抖振问题，还设计了智能规则，对变结构项的强度系数进行自适应调节[10]。李守岩利用SDRE方法设计了等效舵偏角指令，并根据指令分配方法给出了直接力与气动力的指令[11]。

结合大气层外拦截器直接力控制问题开关控制输出的强非线性，本文使用带有超前校正的死区迟滞继电控制律进行开关控制，并使用变结构模型参考自适应方法进行连续控制律设计，以提高开关控制器的工作效率，减少工作能耗。

1 姿态跟踪控制律的设计

拦截器姿态动力学和运动学方程可表示如下：

(1)

(2)

由于拦截器在姿态操作过程中，根据制导律的设计，拦截器的偏航角较大，滚转角小于45°，俯仰角基本在零值附近，可进行小角度假设简化并对原方程进行线性化后，将拦截器的姿态控制回路分为三个独立的通路分别进行控制。

在空间运行阶段，拦截器姿态控制的执行机构是反作用姿控发动机，因此拦截器姿态控制系统是一个典型的“开-关”式非线性控制系统。由于控制系统还存在惯性，所以当采用线性控制时，只要喷嘴一工作就会一直到推进剂耗尽为止。为此，一般采用断续的非线性控制，例如继电控制。在设计继电控制器之前，首先对原系统开关线进行设计。

由于拦截器相对于具有线性力矩输出的导弹不同，其力矩输出为非线性，如何设计开关线，使得系统按照这个开关线对反作用姿控发动机进行打开和关闭操作影响到了整个系统的姿态控制效果和能耗。可以说，开关线的确定是此类飞行器姿态控制设计的重中之重，因此需要对开关线的设定进行进一步的分析。

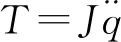
(3)

对这个方程做积分后有

(4)

再做积分，假设有零初始角速度，则有

(5)

(6)

将式(6)的结果代回到式(5)中，就可得到一个将过去角度、角速度和现在角度相联系的总体方程：

(7)

式(7)描述了抛物线状的开关线。然而，为了进行仿真，开关线必须有由两条抛物线组成的实体线那样的形状。因此，开关线方程必须经过改变以达到要求，式(8)是变换后的开关线方程。

(8)

得到系统的开关线设计后，以俯仰通道为例进行控制器设计和分析。这种控制规律一般采用含超前校正网络的死区迟滞继电控制律，考虑到推力器力和力矩输出特性中的死区和迟滞特性，设计控制器如下：

e=(1+ks)(θ-θs)

(9)

(10)

(11)

式中θ1为推力器的死区宽度；θ为实际姿态角；θs为指令姿态角；k为微分系数；h为迟滞系数。

在这种典型的比例微分控制器控制下，系统由初始条件逐渐向里收敛，最后停留在一个稳定范围内。

3 基于滑模变结构控制的模型参考自适应控制器

可看出，上一节所给出的控制输入与姿态信号的微分相关，在指令信号产生突变时，容易造成控制力矩饱和，为解决这种问题，本文采用基于模型参考自适应的方法，将姿态控制回路的输出与参考模型输出进行比较，并对控制器指令进行调整，从而使得控制器姿态角指令更加符合工程需求。

3.1 参考模型设计

通过对参考模型进行设计来间接调节被控对象的跟踪响应，且对于突变的指令可进行平滑处理，避免由于指令的剧烈跳变而导致控制能量的浪费。

由制导系统可以根据拦截器的速度变化需求确定的指令的姿态角，以俯仰通路为例，用θC表示指令姿态角，选取如下参考模型：

(12)

写成状态方程形式：

(13)

在这个参考模型中，时间常数T0和阻尼系数ξ0可以据系统性能指标要求和拦截器允许的姿态机动能力来确定，使得上述二阶系统的状态量ωm保持在一定值之下。

3.2 滑模变结构自适应控制器设计

模型参考自适应控制的系统结构如图1所示，参考模型接收到参考指令r时，响应出参考状态Xm，而实际弹体在接收到输入指令后响应得到实际状态X，变结构模型参考自适应控制器就是通过实际状态与参考状态的差e，实际状态X，参考状态Xm，参考指令r进行弹体指令u的计算方法，这种控制方法的目的就是使实际模型的响应X趋近参考模型响应Xm。

考虑一般的不确定系统：

x∈Rn,u∈Rm,h∈Rn

或简单的模型：

取理想模型：

(14)

设(Am,Bm)可控。定义偏差向量：

e=xm-x

(15)

可以得到其微分方程：

(16)

图1 变结构模型参考控制系统

希望能够做到求u使得模型(14)可跟踪模型(16)的状态，即

下面给出模型跟踪的完全匹配条件：

rank[B]=rank[B,Bm]=rank[B,(Am-A)] (17)

此时：

Am-A=BK1,Bm=BK2,rank(B)=m

(18)

对于模型参考变结构自适应控制系统，控制律u的一般形式为

u=uM+uv

(19)

式中uM=K1x+K2r为匹配控制律；uv为变结构控制律。

引入匹配控制律后，式(16)变为

(20)

就可以使用变结构控制方法求出uv，使得e趋向于0。

以俯仰通道为例，求解变结构控制量uv。俯仰通道近似二阶系统。选取如下参考模型：

(21)

写成状态方程形式，其状态矩阵及控制矩阵为

(22)

将俯仰通道视作二阶环节，则

(23)

将式(20)写成微分方程形式：

(24)

(25)

4 仿真结果与分析

仿真条件设置如下：EKV分离点坐标(-2300， -1300, 6200) km，分离点速度(20，3800，6000) m/s；分离点姿态为，俯仰角84°，偏航角-50°，滚转角66°；轨控发动机推力1500 N，姿控发动机推力50 N；目标初始位置 (-2200，3880，6000) km，初始速度(-200，-3300，5000) m/s；第一次中制导时间854 s，第二次中制导时间904 s，预测命中时间1279.07 s。

为显示本文所给出方法的有效性，本文还给出了基于文献[5]所提出方法的对比仿真结果。文献[7]中，作者采用了类似于比例微分控制的姿态控制器，并通过设定死区减小发动机喷管的开启频率。

EKV与GBI分离后，EKV与被拦截目标的空间轨迹曲线如图2所示。从图2可看到，本文所采用的方法在轨迹上与对比方法较为相似，但是末端拦截精度较高。但是由于文献[7]的对比方法中没有对微分信号做出处理，因此其发动机喷管开启时间更长，作用效率更低。相比之下，本文所采用的带有模型参考自适应控制器的姿态跟踪控制系统可以较好地处理微分指令信号突变引起的喷管开启，尤其是在给定的参考模型动态特性下，系统相应更加迅速，系统跟踪超调更小。

从图3～图5中姿态角的跟踪结果可看到，所设计的控制器能够很好地实现对指令的跟踪，相比文献[7]所给出方法的仿真结果，本文所给出的方法因采用了带有设定参考模型的自适应控制器，指令跟踪的结果有更快速的指令响应、更小的指令超调；从最终脱靶量而言，本文所给出方法在500次蒙特卡洛仿真中的平均拦截脱靶量为0.44 m，能够实现直接碰撞杀伤拦截,对比方法平均脱靶量2.61 m，无法对目标实现直接碰撞拦截。

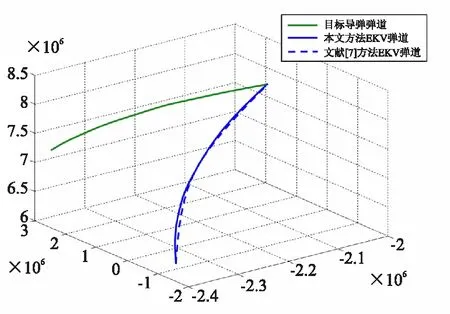
图2 EKV与GBI分离后的拦截轨迹

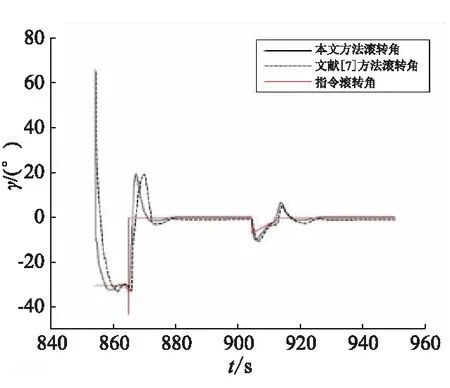
图3 滚转角指令与跟踪曲线

图4 俯仰角指令与跟踪曲线

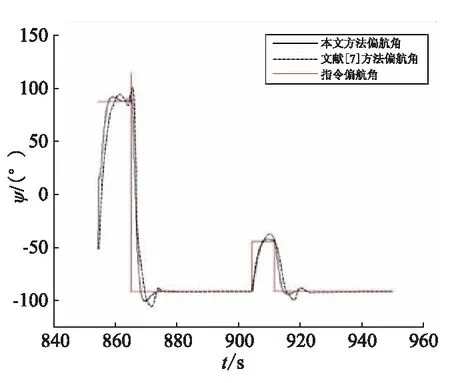
图5 偏航角指令与跟踪曲线

5 结论

本文采用基于滑模变结构控制的模型参考自适应控制器，综合考虑EKV三轴姿态耦合影响，并且通过设计理想二阶模型的参数，实现了期望的响应速度调节。根据数字仿真结果可以看出，相比于对比方法，本文所采用的方法能够以更快速的响应、更小的超调实现指令姿态角度的跟踪。相比于传统方法，本文所给出的方法具有以下几方面突出特点：

(1)模型参考自适应控制器能够更好地实现输出指令的调节，使得控制指令信号更加平稳、高效。

(2)参数化设定的参考模型可以根据实际工程需求进行系统性能设定，方便应用于多种不同工作需求。

(3)本文所设计的方法实现较为简单，对工程实践有一定指导意义。