气动三自由度并联机器人设计与仿真分析

刘 昱，彭 锋，赵国新，张立业，李 菲

(北京石油化工学院信息工程学院，北京 102617)

近年来，并联机器人一直是研究的热点[1-2]，具有承载能力强、微动精度高和逆解简单等优点[3]，广泛应用于医疗机器人、航空、军事和工业自动化等领域。1965年Stewart平台被提出[4]，随后Tsai[5]首次提出3-UPU并联机构，对机构的自由度进行了分析并建立了正逆运动学模型。罗友高等[6]研究了纯平移3-UPU并联机器人的工作空间及其与几何的关系。蒲志新等[7]运用极限搜索法结合MATLAB软件求得机构的工作空间。朱小蓉等[8]研制了一种三自由度并联机构坐标测量机的样机。赵轩等[9]通过模型仿真得到伺服电动缸的缸长变化曲线，显示了平台在六个自由度上的运动规律。李仕华等[10]对一种特殊的3-UPU并联角台机构的瞬时运动特性进行了分析，绘制了上下平台平行时所有运动螺旋的空间分布图。韩雪艳等[11]分析了具有连续转轴的新型3-UPU并联机构的运动特性。

笔者采用三维建模软件设计了3-UPU并联机器人物理模型，该机器人采用气浮无摩擦缸作为驱动器且具有一定的输出力特性[12]。根据该机器人几何关系推导其运动学方程并基于数值解法得到机器人的工作空间；采用遍历法求解机器人各支链旋转角度范围；从而得到该机器人在其工作空间的最大输出力分布情况。结果表明该机器人具有良好的运动学性能。

1 机器人设计与理论分析

1.1 机器人设计

采用三维建模软件设计3-UPU并联机器人物理模型，如图1所示。该机器人的动平台和静平台均为正三角形，3条相同支链的两端分别连接到虎克铰的一侧，虎克铰的另一侧通过几何约束对称连接到2个平台的三角形顶点。其中U代表虎克铰，通过其使两关节之间具有2个独立的相对转动，具有2个转动的自由度；P代表3-UPU并联机器人移动副，其允许两构件沿公共轴线作相对直线运动。

1.2 机构运动学方程

3-UPU并联机器人的运动简图如图2所示。静平台为正三角形A1A2A3，其所在的外接圆圆心为O0，半径为R，支链依次为Pi(i=1，2，3)，其中Ai(i=1，2，3)依次为3条支链的上顶点。建立绝对坐标系O0x0y0z0，x0轴正方向由O0指向A2，z0轴正方向垂直于平面A1A2A3向下，在绝对坐标系下Ai(i=1，2，3)的坐标分别为：

A2(R，0，0)；

动平台为正三角形M1M2M3，其所在的外接圆圆心为O，半径为r，其中Mi(i=1，2，3)依次为3条支链的下顶点。建立局部坐标系Oxyz，x轴正方向由O指向M2，z轴正方向垂直于平面M1M2M3向下，在绝对坐标系Oxyz下Mi(i=1，2，3)的坐标分别为：

M2(r，0，0)；

根据该机器人的几何特点，运用矢量法可得下列矢量方程：

AiMi=-O0Ai+O0O+OMi，(i=1，2，3)

(1)

|AiMi|=li，(i=1，2，3)

(2)

式中：li(i=1，2，3)表示第i个支链的长度。如果设O点的绝对坐标为(x，y，z)，则O0O可以表示为：

O0O=[xyz]T

(3)

O0Ai表示为：

O0A2=[R0 0]T

(4)

OMi表示为：

OM2=[r0 0]T

(5)

令Δ=R-r，得到机器人的运动学逆解：

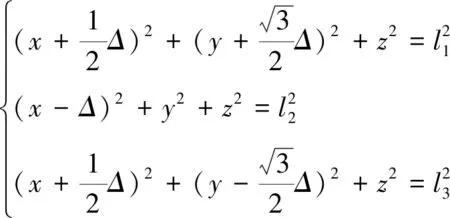
(6)

进一步得到机器人的运动学正解：

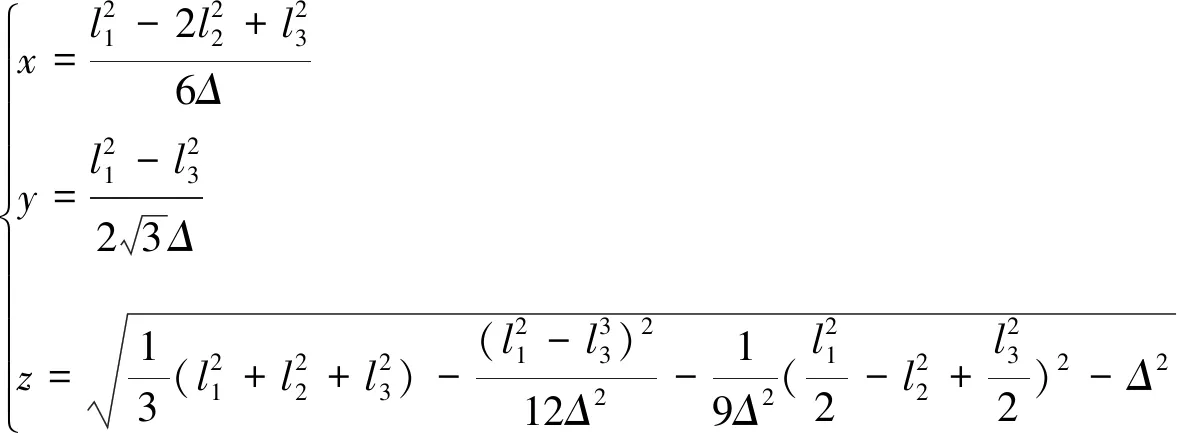
(7)

2 工作空间分析

根据实际支链长度采用遍历法得到满足机器人约束条件的所有坐标点集并可视化显示，从而得到该机器人的工作空间。

已知支链采用的气浮无摩擦缸最小长度lmin=420 mm，最大长度lmax=720 mm，则各支链长度li(i=1，2，3)满足关系式：

lmin≤li≤lmax

(8)

根据该机器人装配关系可知，当其处于初始位置时，支链初始长度l0=570 mm，支链与静平台初始夹角θ0=45°，可以求解出Δ=403.05 mm，通过MATLAB软件仿真计算得到3-UPU并联机器人工作空间，如图3(a)所示，其在xy平面上的投影如图3(b)所示，工作空间为帽子形，空间边界曲线连续且光滑。

工作空间分布如表1所示，其动平台在x，y，z方向最大位移均接近0.5 m。

表1 工作空间分布

3 力学性能分析

为了获取该机器人在其工作空间的力学性能，分别从x，y，z三个方向进行输出力分析，设三个方向输出力为Fx、Fy和Fz。

3.1 x方向输出力分析

根据该机器人的几何关系得到x方向输出力为：

Fx=f(cosθ1cosα1+cosθ2cosα2+

cosθ3cosα3)

(9)

式中：f表示单个气浮无摩擦缸的输出力；θi(i=1，2，3)分别表示各支链与动平台的夹角；αi(i=1，2，3)分别表示各支链在动平台上的投影所在的直线与动平台坐标系x轴的夹角。

已知该气浮无摩擦缸缸径rp=10 mm，气压p=0.5 MPa，可得到单个气缸输出力f约为157 N。

取动平台法向量n0=[0 0 1]T，根据机器人的几何关系得到各支链与动平台的夹角θi(i=1，2，3)为：

θi=arccos(n0·AiMi/(|n0||AiMi|))

(10)

根据机器人的几何关系得到各支链在动平台上投影所在的直线与动平台坐标系x轴的夹角αi(i=1，2，3)为：

(11)

联立式(1)、(2)、(3)、(4)、(5)、(8)、(9)、(10)、(11)可计算得到该机器人在其工作空间上沿x方向输出力范围为Fx∈[132.33 N，301.33 N]。输出力分布图如图4所示，其在xy平面上投影如图4(b)所示。为方便展示，将其分成3个区间，分割参数如表2所示。由图4可以看出，随着z逐渐减小，Fx逐渐增大，在点(0，0，118.11)处Fx取最大值，最大值为301.33 N。

表2 x方向输出力Fx(N)分布表

3.2 y方向输出力分析

同理，根据该机器人的几何关系得到y方向输出力公式为：

Fy=f(cosθ1cosβ1+cosθ2cosβ2+

cosθ3cosβ3)

(12)

式中：βi(i=1，2，3)表示各支链在动平台上的投影所在的直线与动平台坐标系y轴的夹角。由机器人几何关系得：

(13)

联立式(1)、(2)、(3)、(4)、(5)、(8)、(10)(11)、(12)、(13)可计算得到该机器人在其工作空间上沿y方向输出力范围为Fy∈[152.23 N，260.96 N]。输出力分布图如图5所示，其在xy平面上投影如图5(b)所示。为方便展示，将其分成3个区间，分割参数如表3所示。由图5可以看出，随着z逐渐减小，Fy逐渐增大，在点(0，0，118.11)处Fy取最大值，为260.96 N。

表3 y方向输出力Fy(N)分布表

3.3 z方向输出力分析

同理，根据该机器人的几何关系得到z方向输出力公式为：

Fz=f(sinθ1+sinθ2+sinθ3)

(14)

联立式(1)、(2)、(3)、(4)、(5)、(8)、(14)可计算得到该机器人在其工作空间上沿z方向输出力范围为Fz∈[132.45 N，390.29 N]。输出力分布图如图6所示，其在xy平面上投影如图6(b)所示。为方便展示，将其分成3个区间，分割参数如表4所示。由图6可以看出，随着z逐渐增大，Fz逐渐增大，在点(0，0，596.62)处Fz取最大值，为390.29 N。

表4 z方向输出力Fz(N)分布表

4 结论

设计一种具有良好运动学性能的气动3-UPU并联机器人，对其进行运动学分析，并介绍了其特点和目前应用的领域。根据机器人几何关系推导其运动学方程并基于数值解法得到该机器人的工作空间；采用遍历法求解机器人各支链旋转角度范围，从而得到该机器人在其工作空间的最大输出力分布情况。该机器人动平台在x，y，z方向的位移均接近0.5 m；其在点(0，0，118.11)处x，y方向输出力均取最大值，分别为301.33 N和260.96 N，在点(0，0，596.62)处z方向输出力取最大值，为390.29 N。通过分析可知，该机器人具有良好的运动学性能，为进一步的研究提供了依据，在工业自动化等实际应用中具有重要意义。