一种移动对象间方向与距离关系的结合推理方法

董轶群，刘建东，徐文星，王淑鸿

(北京石油化工学院信息工程学院，北京 102617)

方向、距离、拓扑、尺寸等空间关系能够描述现实世界的空间特征。定性空间关系表示与推理一直是人工智能领域的重要研究内容[1]，在智能交通[2-3]、地理信息系统[4]、空间数据库[5]、虚拟空间建模[6]等领域中有着广泛应用。众多应用领域中的问题多是复杂的，如智能交通中通常需要综合路网拓扑信息、交通对象的移动方向以及彼此间的距离信息开展相关应用。然而现有定性空间关系表示与推理研究多是针对对象间单一种类的空间关系[7-17]，难以对复杂空间信息进行有效处理。因此多种空间关系的表示与推理成为近年来的研究热点[18-25]。空间方向和距离关系的结合表示与推理可以有效处理空间位置信息[18，24-25]。然而现有定性方向与距离关系的结合研究多是面向静态空间对象，且难以对后续的空间关系变化做出有效推断。

1 定性方向与距离关系

1.1 OPRAm方向关系模型

OPRAm忽略空间对象的维度与尺寸，将1个移动的空间对象抽象为1个带方向的点，称为有向点，记为：

S=(PS,φS)

(1)

其中：PS为平面坐标，表示S的位置，即PS=(xS，yS)；φS是从x轴正向逆时针旋转到S所形成的旋转角，表示S的移动方向，该旋转角取值区间是[0， 2π)上的循环群。

定义1给定粒度参数m∈N+，有向点A、B之间的OPRAm关系记为：

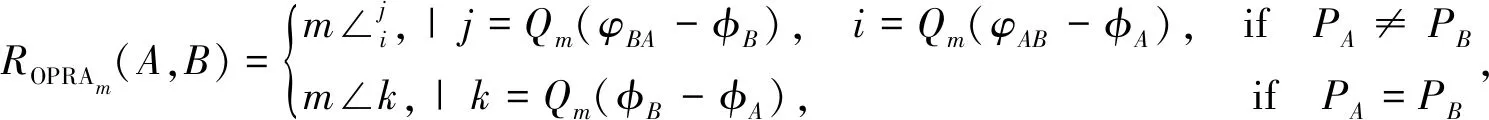
(2)

(3)

式(2)中：i、j、k，即Qm(δ)的取值，均定义在4m循环群上。每个OPRAm(A，B)取值称为1个基本OPRAm方向关系。

1.2 定性距离变化

面向二维平面空间中移动的点对象，将对象间的欧氏距离变化定性地分为“变大”、“变小”、“不变”和“不确定”共4种情况，分别用further、nearer、unchange、uncertain表示，构成的集合记为Udis，则有：

Udis={further，nearer，unchange，uncertain}

(4)

下面着重研究OPRA2方向关系对这4种定性距离变化的约束作用。

2 OPRA2方向关系对定性距离变化的约束作用

2.1 移动对象间的相对位置关系Rpos-pair

对于有向点A=(PA，φA)与B=(PB，φB)，用A、B分别表示以A、B为起点的射线；用AB表示以A为起点、B为终点的一条有向线段；用CAB表示以A为圆心，以A与B之间的欧氏距离(|AB|)为半径的圆。首先根据A到B的投影情况定义B与CAB之间的位置关系，如图2所示。

定义2对于有向点A=(PA，φA)与B=(PB，φB)，PA≠PB，将A向B所在直线投影得投影点Proj(A)，若|AProj(A)|=|AB|，即Proj(A)=B，则称B与CAB相切，记为t(B，CAB)。

定义3对于有向点A=(PA，φA)与B=(PB，φB)，PA≠PB，将A向B所在直线投影得投影点Proj(A)，若|AProj(A)| <|AB|且Proj(A)∈B，则称B与CAB相割，记为c(B，CAB)。

定义4对于有向点A=(PA，φA)与B=(PB，φB)，PA≠PB，将A向B所在直线投影得投影点Proj(A)，若|AProj(A)| < |AB| 且Proj(A)∉B，则称B与CAB相离，记为d(B，CAB)。

特殊地，当PA=PB时，有|AB|=0，此时圆CAB相当于一点，用定义5描述这种特殊情况。

定义5对于有向点A=(PA，φA)与B=(PB，φB)，若PA=PB，则称B与CAB同置，记为i(B，CAB)。

很显然，若有i(B，CAB)则有i(A，CBA)。

定义6对于任意2个有向点A、B，由B与CAB之间的位置关系所构成的集合记为Rpos， 有：

Rpos={t，c，d，i}，

(5)

称Rpos中的每个元素为1个基本Rpos关系。

由图2可知，任意2个有向点A、B之间必定满足1种基本Rpos关系且仅满足1种，即关系集合Rpos是完备互斥的。为更加全面准确地描述任意2个有向点A、B之间的空间信息，不仅需要B与CAB之间的位置关系，还需要A与CBA之间的位置关系。

定义7Rpos-pair为Rpos上的1个有序二元关系，定义如下：

Rpos-pair={，，，，，，，，，}

(6)

称Rpos-pair中每个元素为1个基本Rpos-pair关系。

对于任意2个有向点A、B，二者满足1种基本Rpos-pair关系，其语义如表1所示。

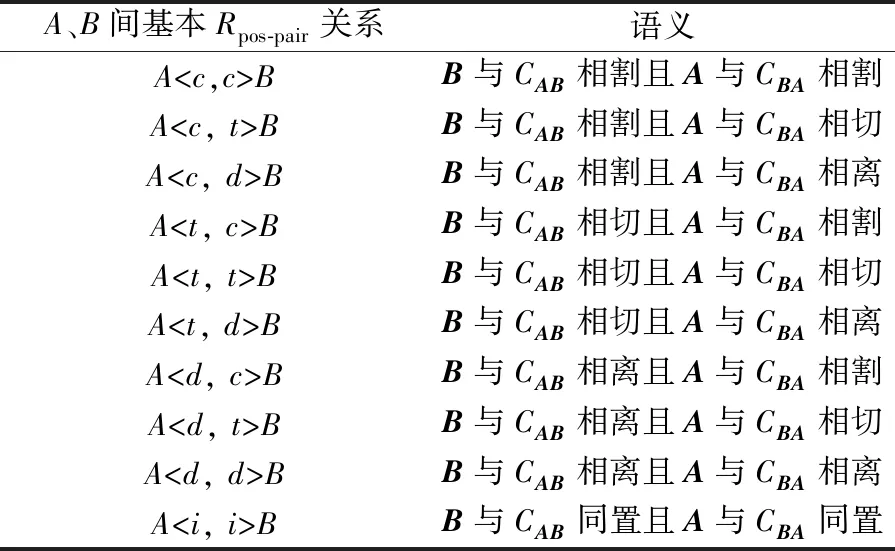
表1 基本Rpos-pair关系语义表

由于Rpos是完备互斥的，因此易知Rpos-pair也是完备互斥的。

2.2 Rpos-pair对定性距离变化的约束

对于任意2个有向点A=(PA，φA)与B=(PB，φB)，在不同基本Rpos关系下，φB与φAB间满足命题1～命题3。

命题1对于任意2个有向点A=(PA，φA)与B=(PB，φB)，若有d(B，CAB)，φAB∈[0，2π)，则有φB∈(φAB-π/2，φAB+π/2)。

证明当φAB∈[0，π/2)时，若d(B，CAB)，由定义4可知，Proj(A)应位于CAB上过B点的切线的下方，因此φB∈(φAB-π/2，φAB+π/2)，如图3所示。

类似地，若d(B，CAB)，当φAB∈[π/2，π)，φAB∈[π，3π/2)，φAB∈[3π/2，2π)时，均有φB∈(φAB-π/2，φAB+π/2)。

证毕。

同理可证命题2与命题3成立。

命题2对于任意2个有向点A=(PA，φA)与B=(PB，φB)，若c(B，CAB)，φAB∈[0， 2π)，则有φB∈(φAB+π/2，φAB+3π/2)。

命题3对于任意2个有向点A=(PA，φA)与B=(PB，φB)，若t(B，CAB)，φAB∈[0，2π)，则有φB=φAB+(2k+1)π/2，k∈Z。

定理1任意2个有向点A=(PA，φA)与B=(PB，φB)，分别沿着各自方向移动LA、LB后到达A′=(PA′，φA)、B′=(PB′，φB)，若PA≠PB且A与CBA以及B与CAB之间不存在相切关系，当LA=LB=0时，|A′B′|2的增量Δz满足：

Δz≈-2((xB-xA)cosφA+(yB-yA)sinφA)ΔLA+2((xB-xA)cosφB+(yB-yA)sinφB)ΔLB

(7)

其中：φA，φB，φAB∈[0，2π)，PA=(xA，yA)，PB=(xB，yB)，PA′=(xA′，yA′)，PB′=(xB′，yB′)，ΔLA≥0与ΔLB≥0分别为一微小时间间隔内LA、LB的增量。

证明由两点间距离公式可知：

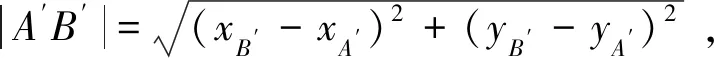
(8)

构造二元函数：

z=f(LA，LB)=|A′B′|2，

(9)

将式(8)带入式(9)有：

f(LA，LB)=(xB′-xA′)2+(yB′-yA′)2

(10)

由于xB′=LBcosφB+xB，yB′=LBsinφB+yB，xA′=LAcosφA+xA，yA′=LAsinφA+yA，如图4所示，因此有：

f(LA，LB)=(LBcosφB+xB-LAcosφA-xA)2+(LBsinφB+yB-LAsinφA-yA)2

(11)

整理后得：

f(LA，LB)=(LBcosφB-LAcosφA)2+(LBsinφB-LAsinφA)2+2(LBcosφB-LAcosφA)(xB-xA)+2(LBsinφB-LAsinφA)(yB-yA)+(xB-xA)2+(yB-yA)2

(12)

函数f(LA，LB)描述了A、B沿着各自方向移动的距离(分别为LA、LB)与A、B移动后二者间距离(即|A′B′|)之间的关系。对f(LA，LB)求一阶偏导数有：

fLA=2(LA-LBcos (φA-φB)-(xB-xA)cosφA-(yB-yA)sinφA)

(13)

fLB=2(LB-LAcos (φA-φB)+(xB-xA)cosφB+(yB-yA)sinφB)

(14)

因此f(LA，LB)在LA=LB=0处的全增量Δz满足：

Δz≈dz=-2((xB-xA)cosφA+(yB-yA)sinφA)ΔLA+2((xB-xA)cosφB+(yB-yA)sinφB)ΔLB

(15)

若PA=PB，则xB=xA，yB=yA，此时无论φA、φB，ΔLA与ΔLB如何取值，式(15)中Δz恒为0，即Δz无法表示A、B间的距离增量。

若PA≠PB且xB=xA，则yB≠yA。当t(A，CBA)时，必有φA=kπ，k∈Z，因此sinφA=0，使得无论ΔLA如何取值，式(15)中ΔLA系数恒为0，此时Δz无法描述ΔLA对A、B间距离增量的约束作用。

若PA≠PB且xB≠xA，式(15)可整理为：

Δz≈-2(cosφA+tanφABsinφA)(xB-xA)×ΔLA+2(cosφB+tanφABsinφB)(xB-xA)ΔLB

(16)

当t(A，CBA)时，由命题3可知，cos(φAB-φA)=0，因此cosφA=-tanφABsinφA，使得无论ΔLA如何取值，式(16)中ΔLA系数恒为0，Δz无法描述ΔLA对A、B间距离增量的约束作用。同理，t(B，CAB)时情况类似。 证毕。

接下来，利用定理1研究任意2个有向点在不同基本Rpos-pair关系下的定性距离变化。

推论1对于任意2个有向点A、B，若AB，在A、B分别沿着各自当前方向移动某一微小时间间隔后，二者之间距离将不变或变小。

证明设A、B分别沿各自当前方向移动了LA、LB到达A′、B′，经过某一微小时间间隔后到达A″、B″，期间LA、LB的增量分别为ΔLA≥0、ΔLB≥0。已知AB，当LA=LB=0时基于定理1中式(7)对ΔLA、ΔLB分情况讨论：

(1)当limΔLA=0，limΔLB≠ 0时，已知c(B，CAB)，由命题2可知φB∈(φAB+π/2，φAB+3π/2)，此时对于φAB在[0，2π)内的任意取值，均有Δz<0。当LA=LB=0时，有|A′B′|=|AB|。由于Δz是函数f(LA，LB)=|A′B′|2在(0，0)处的全增量，因此Δz<0意味着|A″B″|2-|A′B′|2<0，即有|A″B″|< |AB|，如图5所示，因此A、B之间距离将变小。

(2)与(1)情况类似，当limΔLB=0，limΔLA≠ 0时，由已知c(A，CBA)与命题2可知Δz<0，因此二者之间距离将变小。

(3)当limΔLB=limΔLA=0时，可知Δz=0，这意味着在微小时间间隔内A、B静止，因此二者之间距离将不变。

综上所述，若AB，当至少一方距离增量不为0时，二者之间距离将变小；当二者距离增量均为0时，二者之间距离将不变。证毕。

类似地，基于命题1可证明推论2成立。

推论2对于任意2个有向点A、B，若AB，在A、B分别沿着各自当前方向移动某一微小时间间隔后，二者之间距离将不变或变大。

推论3对于任意2个有向点A、B，若AB，在A、B分别沿着各自当前方向移动某一微小时间间隔后，二者之间距离变化不确定。

证明设A、B分别沿着各自当前方向移动了LA、LB到达A′、B′，经过某一微小时间间隔后到达A″、B″，期间LA、LB的增量分别为ΔLA≥0、ΔLB≥0，对ΔLA、ΔLB分情况讨论：

(1)与定理1中式(15)之前的证明部分相同，已知AB，因此有PA≠PB，c(B，CAB)。若limΔLA=0，limΔLB≠ 0，此时与推论1证明中的(1)相同，可知二者之间距离将变小。

(2)已知t(A，CBA)，在证明定理1时已说明，此时cos(φAB-φA)=0，使得式(15)中ΔLA的系数恒为0，无法用式(15)讨论距离变化。当PA≠PB，LA=LB=0时，可知|A′B′|=|AB|;当limΔLB=0，limΔLA≠ 0时，可知B″与B′近似相等，如图6所示，因此有|A″B″| ≈ |A″B′|。因为|A″B″| > |A′B′|，即|A″B″| > |AB|，因此二者之间距离将变大。

(3)当limΔLA=limΔLB=0时，A、B静止，二者之间距离将不变。

综上所述，若AB，无法确定二者之间的距离变化。证毕。

类似地，可证明推论4～推论9成立：

推论4对于任意2个有向点A、B，若AB，在A、B分别沿着各自当前方向移动某一微小时间间隔后，二者之间距离变化不确定。

推论5对于任意2个有向点A、B，若AB，在A、B分别沿着各自当前方向移动某一微小时间间隔后，二者之间距离变化不确定。

推论6对于任意2个有向点A、B，若AB，在A、B分别沿着各自当前方向移动某一微小时间间隔后，二者之间距离将不变或变大。

推论7对于任意2个有向点A、B，若AB，在A、B分别沿着各自当前方向移动某一微小时间间隔后，二者之间距离变化不确定。

推论8对于任意2个有向点A、B，若AB，在A、B分别沿着各自当前方向移动某一微小时间间隔后，二者之间距离将不变或变大。

推论9对于任意2个有向点A、B，若AB，在A、B分别沿着各自当前方向移动某一微小时间间隔后，二者之间距离将不变或变大。

推论10对于任意2个有向点A、B，若AB，在A、B分别沿着各自当前方向移动某一微小时间间隔后，二者之间距离将不变或变大。

证明若AB，则PA=PB，若二者的移动方向与速度均相同，则后续距离保持不变；若二者移动方向或速度不同，则后续距离将变大。证毕。

2.3 Rpos-pair与OPRA2的对应关系

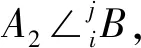
证明由命题1可知，对任意2个有向点A、B，若d(B，CAB)，则有φB∈(φAB-π/2，φAB+π/2)。令δ=(φBA-φB)，由式(2)可知j=Qm(δ)，由于φBA=φAB+π，因此δ∈(π/2，3π/2)，由式(4)可知j∈{3，4，5}。证毕。

类似地，可证命题5与命题6成立。

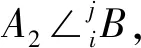
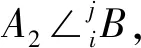
命题7对于2个有向点A、B，若i(B，CAB)，则A2∠kB，其中k∈{0，1，2，3，4，5，6，7}。

证明由定义5可知，若有向点A、B对应的射线与圆之间存在同置关系，则有PA=PB，进而由定义1可知A2∠kB，其中k∈{0，1，2，3，4，5，6，7}。证毕。

基于命题4～命题7可归纳出基本Rpos关系与OPRA2方向关系之间的对应表、基本Rpos-pair关系与OPRA2方向关系之间的对应关系，分别如表2和表3所示。

表2 基本Rpos关系与OPRA2方向关系对应表

Table 2 The Corresponding Table of BasicRposRelations and OPRA4Direction Relations

基本Rpos关系OPRA2方向关系d(B,CAB)Ud2={2∠ji|i,j∈N,0≤i≤7,3≤j≤5}c(B,CAB)Uc2={2∠ji|i∈N,0≤i≤7,j∈{0,1,7}}t(B,CAB)Ut2={2∠ji|i∈N,0≤i≤7,j∈{2,6}}(B,CAB)Ui2={2∠k|k∈N,0≤k≤7}

表3 基本Rpos-pair与OPRA2方向关系对应表

2.4 OPRA2对定性距离变化的约束

基于2.2节与2.3节中结论，借助于基本Rpos-pair关系可以建立起OPRA2方向关系与定性距离变化的内在联系，如表4所示。

表4 OPRA2方向关系与定性距离变化对应表

Table 4 The Corresponding Table of OPRA4Direction Relations and Qualitative Distance Changes

OPRA2方向关系定性距离变化Udd2={2∠ji|i,j∈{3,4,5}}{further, unchange}Udt2={2∠ji|i∈{2,6},j∈{3,4,5}}{further, unchange}Udc2={2∠ji|i∈{0,1,7},j∈{3,4,5}}{uncertain}Utd2={2∠ji|i∈{3,4,5},j∈{2,6}}{further,unchange}Utt2={2∠ji|i,j∈{2,6}}{further, unchange}Utc2={2∠ji|i∈{0,1,7},j∈{2,6}}{uncertain}Ucd2={2∠ji|i∈{3,4,5},j∈{0,1,7}}{uncertain}Uct2={2∠ji|i∈{2,6},j∈{0,1,7}}{uncertain}Ucc2={2∠ji|i,j∈{0,1,7}}{nearer, unchange}Uii2={2∠k|k∈N,0≤k≤7}{further, unchange}

表4中给出了OPRA2方向关系全集的1个划分：

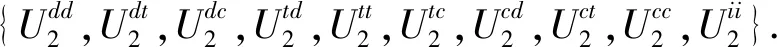
(17)

因此，若已知A、B之间的基本OPRA2方向关系，可参照表4对二者间定性距离变化进行相应的判断。

3 基于OPRA2推断定性距离变化算法

下面给出算法OPRA2-Distance的伪代码，对于任意2个移动对象，当已知二者当前基本OPRA2方向关系时，用该算法对二者定性距离变化进行推断。

算法 OPRA2-Distance(R)

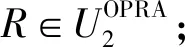
输出：有向点A、B间的定性距离变化D∈2Udis。

1.D←∅;

3. if (((i>=2 &&i<=6) && (j>=3 &&j<=5)) || ((i>=2 &&i<=6) && (j==2||j==6)))

4.D←{unchange， further};

5. if ((("Si==0||i==1||i==7) &&(j>=2 &&j<=6)) || ((j==0||j==1||j==7)&&(i>=2 &&i<=6)))

6.D←{uncertain};

7. if ((i==0||i==1||i==7) && (j==0||j==1||j==7))

8.D←{unchange， nearer};

9. else

10.D←{unchange， further}．

推论11对于任意2个有向点A、B，若已知二者间的基本OPRA2方向关系，算法OPRA2-Distance能够正确推断出后续微小时间间隔内二者间基于Udis的定性距离变化。

证明设有向点A、B满足基本OPRA2方向关系R。

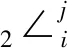
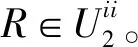
4 结论

面向移动空间对象，针对OPRA2方向关系与定性距离变化的结合推理问题，首先通过定义射线与圆之间的Rpos关系描述目标对象相对于参照对象的移动方向；然后通过组合方式定义了Rpos-pair关系，用以描述2个移动对象间的相对Rpos关系；分别研究并证明了基本Rpos-pair关系对定性距离变化的约束作用、基本Rpos-pair关系与OPRA2方向关系之间的对应关系，进而借助于基本Rpos-pair关系建立起OPRA2方向关系与定性距离变化之间的内在联系。在此基础上提出一种基于基本OPRA2方向关系推理定性距离变化的方法，并证明了方法的正确性。